高三数学综合练习综合练习(二)
(考试时间120分钟, 满分150分)
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 15 | 16 | 17 | 18 | 19 | 20 | ||||
| 分数 | |||||||||
第Ⅰ卷 (选择题共40分)
参考公式:
如果事件A、B互斥,那么 P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率 ![]() .
.
球的表面积公式S=4πR2 , 球的体积公式 V = ![]() πR3,其中R表示球的半径.
πR3,其中R表示球的半径.
| 得分 | 评卷人 |
一、选择题:本大题共8小题,每小题5分,共40分. 在每小题的
4个选项中,只有一项是符合题目要求的.
(1) 满足条件{1,2}∪M={1,2,3}的所有集合M的个数是 ( )
(A)1 (B)2 (C)3 (D)4
(2) 设条件p:x= x;条件q:x2+x≥0,那么p是q的 ( )
(A)充分非必要条件 (B)必要非充分条件
(C)充分且必要条件 (D)非充分非必要条件
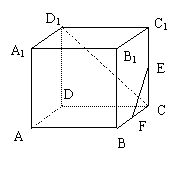 (3) 正方体ABCD-A1B1C1D1中,E、F分别是棱C1C与
(3) 正方体ABCD-A1B1C1D1中,E、F分别是棱C1C与
BC的中点,则直线EF与直线D1C所成角的大小是
( )
(A)45° (B)60° (C)75° (D)90°
(4) 要得到函数y=2sin(2x -![]() )的图像,只需将函数y=2sin2x的图像 ( )
)的图像,只需将函数y=2sin2x的图像 ( )
(A) 向左平移![]() 个单位 (B)
向右平移
个单位 (B)
向右平移![]() 个单位
个单位
(C) 向左平移![]() 个单位 (D)
向右平移
个单位 (D)
向右平移![]() 个单位
个单位
(5) 将直线![]() 绕原点按顺时针方向旋转
绕原点按顺时针方向旋转![]() ,所得直线与圆
,所得直线与圆![]() 的位置关系是
( )
的位置关系是
( )
(A) 直线与圆相离 (B) 直线与圆相交但不过圆心
(C) 直线与圆相切 (D) 直线过圆心
(6) 某校高一学生进行演讲比赛,原有5名同学参加比赛,后又增加两名同学参赛,如果保持原来5名同学比赛顺序不变,那么不同的比赛顺序有 ( )
(A)12种 (B)30种 (C)36种 (D)42种
(7) 椭圆M:![]() =1 (a>b>0) 的左、右焦点分别为F1、F2,P为椭圆M上任一点,且
=1 (a>b>0) 的左、右焦点分别为F1、F2,P为椭圆M上任一点,且![]() 的最大值的取值范围是[2c2,3c2],其中
的最大值的取值范围是[2c2,3c2],其中![]() . 则椭圆M的离心率e的取值范围是
( )
. 则椭圆M的离心率e的取值范围是
( )
(A)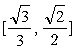 (B)
(B)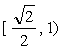 (C)
(C)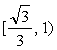 (D)
(D)![]()
(8) 数列![]() 中,
中,![]() ,
,![]() 是方程
是方程![]() 的两个根,则数列
的两个根,则数列![]() 的前
的前![]() 项和
项和![]() ( )
( )
(A)![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D)![]()
第II卷(非选择题 共110分)
| 得分 | 评卷人 |
二、填空题:本大题共6小题,每小题5分,共30分.将答案填在题中
横线上.
(9) lg8+3lg5的值为 .
(10) 已知函数![]() 的反函数
的反函数![]() ,则方程
,则方程![]() 的解是 .
的解是 .
(11) 一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积是![]() ,那么这个球的半径是 ,三棱柱的体积是
.
,那么这个球的半径是 ,三棱柱的体积是
.
(12) 定义运算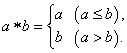 则对x∈R,函数f(x)=1*x的解析式为f(x)= .
则对x∈R,函数f(x)=1*x的解析式为f(x)= .
(13) 已知![]() ,则c =
, a= .
,则c =
, a= .
(14) 一个总体中的100个个体号码为0,1,2,…,99,并依次将其分为10个小组。要用系统抽样方法抽取一个容量为10的样本,规定:如果在第1组(号码为0~9)随机抽取的号码为m ,那么依次错位地得到后面各组的号码,即第k组中抽取的号码的个位数为m+k-1或m+k-11(如果m+k≥11).若第6组中抽取的号码为52, 则m= .
三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.
| 得分 | 评卷人 |
(15)(本小题满分13分)
已知向量 m = (cos![]() ,
,![]() cos
cos![]() ),n = (sin
),n = (sin![]() ,cos
,cos![]() ),函数f(x) = m·n .
),函数f(x) = m·n .
(Ⅰ)求f(x)的解析式;
(Ⅱ)求f(x)的单调递增区间;
(Ⅲ)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
| 得分 | 评卷人 |
(17)(本小题满分13分)
某大学的研究生入学考试有50人参加,其中英语与政治成绩采用5分制,设政治成绩为x,英语成绩为y,结果如下表:
|
x | 英 语 | |||||
| 1分 | 2分 | 3分 | 4分 | 5分 | ||
| 政 治 | 1分 | 1 | 3 | 1 | 0 | 1 |
| 2分 | 1 | 0 | 7 | 5 | 1 | |
| 3分 | 2 | 1 | 0 | 9 | 3 | |
| 4分 | 1 | b | 6 | 0 | a | |
| 5分 | 0 | 0 | 1 | 1 | 3 | |
(Ⅰ)求a +b的值;
(Ⅱ)求政治成绩为4分且英语成绩为3分的概率;
(Ⅲ)若“考生的政治成绩为4分” 与“英语成绩为2分”是相互独立事件,求a、b的值;
(Ⅳ)若y的数学期望为![]() ,求a、b的值.
,求a、b的值.
| 得分 | 评卷人 |
(18)(本小题满分13分)
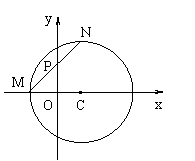
如图,已知圆C:![]() ,设M为圆C与x轴负
,设M为圆C与x轴负
半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.
 (Ⅰ)当r=2时, 求满足条件的P点的坐标;
(Ⅰ)当r=2时, 求满足条件的P点的坐标;
![]() (Ⅱ)当r∈(1,+∞)时,求点N的轨迹G的方程;
(Ⅱ)当r∈(1,+∞)时,求点N的轨迹G的方程;
(Ⅲ)过点P(0,2)的直线l与(Ⅱ)中轨迹G相交于两个不同
的点E、F,若![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
| 得分 | 评卷人 |
(19)(本小题满分14分)
设对于任意实数![]() 、
、![]() ,函数
,函数![]() 、
、![]() 满足
满足![]() 且
且![]() ,
,
![]() ,
,![]() .
.
(Ι)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(ΙΙ)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和Sn;
项和Sn;
(ΙΙΙ)已知![]() ,设
,设![]() ,是否存在整数
,是否存在整数![]() 和
和![]() ,使得对任意正整数
,使得对任意正整数![]() 不等式
不等式![]() <
<![]() <
<![]() 恒成立?若存在,分别求出
恒成立?若存在,分别求出![]() 和
和![]() 的集合,并求出
的集合,并求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
| 得分 | 评卷人 |
(20)(本小题满分14分)
已知函数![]() ,
,![]()
(Ⅰ)若![]() 在区间
在区间![]() 上的最大值为1,最小值为
上的最大值为1,最小值为![]() ,求
,求![]() 、
、![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,求经过点![]() 且与曲线
且与曲线![]() 相切的直线
相切的直线![]() 的方程;
的方程;
(Ⅲ)设函数![]() 的导函数为
的导函数为![]() ,函数
,函数![]() ,试判断函数
,试判断函数![]() 的极值点个数,并求出相应实数
的极值点个数,并求出相应实数![]() 的范围.
的范围.
2005-2006高三数学综合练习(二)参考答案及评分标准(理科)
2006.4
一.选择题(本大题共8小题,每小题5分,共40分)
(1) D (2) A (3) B (4) D
(5) C (6) D (7) A (8) D
二.填空题(本大题共6小题,每小题5分,共30分)
(9) 3 (10) x
=1
(11) 2,48![]()
(12)f(x)=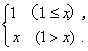 (13) -3,1 (14) 7
(13) -3,1 (14) 7
三.解答题(本大题共6小题,共80分)
15. 解:(Ⅰ)![]()
=![]() =
=![]() . ………………5分
. ………………5分
(Ⅱ)由![]() ≤
≤![]() ≤
≤![]() 得
得![]() ≤
≤![]() ≤
≤![]() .
.
∴![]() 的单调增区间为[
的单调增区间为[![]() ,
,![]() ](
](![]() ).
………9分
).
………9分
(Ⅲ)![]() =
=![]() ≥
≥![]() =
=![]() ,
,
∵![]() 是△ABC的内角, ∴
是△ABC的内角, ∴![]() .
.
∴![]() .
.
∴![]() ≤1. ∴
≤1. ∴![]() 的值域是
的值域是![]() . …………13分
. …………13分
16. 方法1:
(Ⅰ)证明:∵∠BAD=90°,AB=2![]() ,AE=2,∴∠AEB=60°.
,AE=2,∴∠AEB=60°.
∵∠ADC=60°,CD、BE共面,∴CD∥BE.
又CD![]() 面PBE,∴CD∥面PBE.
…………4分
面PBE,∴CD∥面PBE.
…………4分
(Ⅱ)解:在面APD内作PO⊥AD,垂足为O,
∵侧面APD⊥底面ABCD,∴PO⊥底面ABCD.
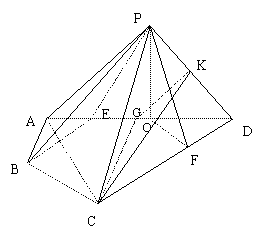 在面PCD内作PF⊥CD,垂足为F,连结OF,
在面PCD内作PF⊥CD,垂足为F,连结OF,
∴∠PFO是二面角P-CD-A的平面角.
依条件易求出PD=2![]() ,
,
由Rt△APD∽Rt△POD,
得PO=![]() ,OD=
,OD=![]() ,
,
解Rt△OFD得OF=![]() . ∴tan∠PFO=
. ∴tan∠PFO=![]() =
=![]() .
.
∴∠PFO=arctan![]() . 即二面角P-CD-A的大小为arctan
. 即二面角P-CD-A的大小为arctan![]() . ……………9分
. ……………9分
(Ⅲ)解法1: 连结AC, 设点C到平面ABP的距离为hC,
∵VC-ABP=![]() hC·S△ABP=VP-ABC=
hC·S△ABP=VP-ABC=![]() PO·S△ABC, ∴hC=
PO·S△ABC, ∴hC=![]() .
.
由(Ⅱ)知PO⊥底面ABCD, PD=2![]() ,PO=
,PO=![]() .
.
在平面ABCD内作CG⊥AD,垂足为G,易求出CG=4![]() ,并知G为AD中点.
,并知G为AD中点.
∴点C到AB的距离等于AG=4.
∴S△ABC=![]() AB×AG =
AB×AG =![]() ×4=4
×4=4![]() . S△ABP=
. S△ABP=![]() AB×AP=6
AB×AP=6![]() .
.
∴hC=![]() =
=![]() .
.
∵G为Rt△APD斜边中点,∴PG=4.
∵CG⊥AD,垂足为G,且侧面APD⊥底面ABCD,∴CG⊥面APD.
∴CG⊥PG. ∴PC=8.
设PC与面ABP所成角为θ,则sinθ=![]() .
.
即PC与面ABP所成角的大小等于arcsin![]() .
……………………………13分
.
……………………………13分
解法2:
在面ABCD内作CG⊥AD,垂足为G, 又AB⊥AD,且AB、CG共面,∴AB∥CG.
∵面APD⊥面ABCD,∴CG⊥面APD.
在面APD内作GK⊥PD,垂足为K,连结CK, ∴CK⊥PD.
又AP⊥PD,且AP,GK共面,∴AP∥GK.
∵AB∩AP=A,CG∩GK=G,∴面ABP∥面GCK.
∴PC与面ABP所成的角等于PC与面GCK所成角.
∵GK⊥PD,CK⊥PD,且CG∩GK=G, ∴PK⊥面GCK.
∴∠PCK是PC与面CGK所成的角.
易计算出G为AD中点,∴K为PD中点.
∵PD=2![]() ,∴PK=KD=
,∴PK=KD=![]() . ∴CK=
. ∴CK=![]() . ∴tan∠PCK=
. ∴tan∠PCK=![]() =
=![]() =
=![]() .
.
即PC与面ABP所成角的大小等于arctan![]() . (等于arcsin
. (等于arcsin![]() )……………13分
)……………13分
(解法3提示:延长AB、DC,设交点为M,连结PM,过C作CH∥PD,HC交PM于H,证明∠HPC是PC与面ABP所成的角,….)
方法2:
如图建立空间直角坐标系.
所以各点的坐标是A(0,-![]() ,0),B(2
,0),B(2![]() ,-
,-![]() ,0),C(4
,0),C(4![]() ,-
,-![]() ,0),
,0),
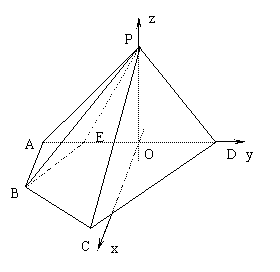 D(0,
D(0,![]() ,0),E(0,-
,0),E(0,-![]() ,0),P(0,0,
,0),P(0,0,![]() )
)
容易求出平面PAB的一个法向量为n1= (0,![]() ,-
,-![]() ),
),
平面PCD的一个法向量为n2= (![]() ,3,
,3,![]() ),
),
平面APD的一个法向量为n3= (1,0,0),
平面ABCD的一个法向量为n4= (0,0,1),
(Ⅰ)证明:容易求出![]() =(-4
=(-4![]() ,4,0),
,4,0),
平面PBE的一个法向量为n3= (-![]() ,-
,-![]() ,
,![]() ),
),
∵![]() ·n3=(-4
·n3=(-4![]() ,4,0)·(-
,4,0)·(-![]() ,-
,-![]() ,
,![]() )= (-4
)= (-4![]() )(-
)(-![]() )+4(-
)+4(-![]() )=0,
)=0,
∴![]() ⊥n3. 又CD
⊥n3. 又CD![]() 平面PBE, ∴CD∥平面PBE. ………………………4分
平面PBE, ∴CD∥平面PBE. ………………………4分
(Ⅱ)解:设所求二面角为θ,
∵n2·n4= (![]() ,3,
,3,![]() )·(0,0, 1)=
)·(0,0, 1)= ![]() ,n2n4=
,n2n4=![]() =
=![]() ,
,
∴cosθ=![]() =
=![]() . ∴θ=arccos
. ∴θ=arccos![]() .
.
∴所求二面角的大小为arccos![]() .(等于arctan
.(等于arctan![]() ) ………………………9分
) ………………………9分
(Ⅲ)设PC与平面APB所成的角为α,
则![]() 与平面APB法向量n1所成的角为
与平面APB法向量n1所成的角为![]() -α,或α-
-α,或α-![]() .
.
∵![]() = (4
= (4![]() ,-
,-![]() ,-
,-![]() ),
),
∴![]() ·n1= (4
·n1= (4![]() ,-
,-![]() ,-
,-![]() )· (0,
)· (0,![]() ,-
,-![]() )=
)=![]() ,
, ![]() n1=8×
n1=8×![]() =
=![]() .
.
∴cos(![]() -α)=
-α)=![]() ×
×![]() =
=![]() . 即sinα=
. 即sinα=![]() .
.
∴ PC与面ABP所成角的大小等于arcsin![]() .
…………………13分
.
…………………13分
17. 解:(Ⅰ)考生总人数是50,因此表中标出的总人数也应是50,所以a +b+47=50,
故a +b=50-47=3; ………………………………3分
(Ⅱ)从表中可以看出,“政治成绩为4分且英语成绩为3分”的考生人数为6人,所以其概率为![]() .
………………………………6分
.
………………………………6分
(Ⅲ)因为若“考生的政治成绩为4分” 与“英语成绩为2分”是相互独立事件,
所以P(x=4,y=2)= P(x=4)·P(y=2),即![]() ,
,
解得: b=1,a=2. …………………………………10分
(Ⅳ)由已知![]() ,解得:a=1,b=2.
,解得:a=1,b=2.
………………………………13分
18. (Ⅰ)解一:
由已知得,r=2时,可求得M点的坐标为M(-1,0)
设P(0,b),则由![]() (或用勾股定理)得:
(或用勾股定理)得:![]()
∴![]()
![]() 即点P坐标为(0,
即点P坐标为(0,![]() )
………………………………4分
)
………………………………4分
解二:同上可得M(-1,0)
设N(x,y), 则![]() 解得N(1,
解得N(1,![]() )
)
∴![]() MN的中点P坐标为(0,
MN的中点P坐标为(0,![]() ) ………………………………4分
) ………………………………4分
(Ⅱ)解一:设N(x,y),
由已知得,在圆方程中令y=0,求得M点的坐标为(![]() ,0)
,0)
设P(0,b),则由![]() (或用勾股定理)得:
(或用勾股定理)得:![]()
∵点P为线段MN的中点,∴![]() ,
,![]() ,又r>1
,又r>1
∴点N的轨迹方程为![]() ………………………………8分
………………………………8分
解二:设N(x,y),
同上可得M(![]() ,0),则
,0),则
![]() ,消去r,又r>1
,消去r,又r>1
∴点N的轨迹方程为![]() ………………………………8分
………………………………8分
(Ⅲ)依题意得直线l的斜率存在且不为0,
设直线l的方程为y=kx+2,E(x1,y1),F(x2,y2)
由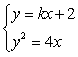 ,得k2x2+(4k-4)x+4=0.
,得k2x2+(4k-4)x+4=0.
由△=-32k+16>0,得k<![]() .
.
∵![]() ,∴(x1-1)(x2-1)+y1y2>0.
,∴(x1-1)(x2-1)+y1y2>0.
∴(k2+1)x1x2+(2k-1)(x1+x2)+5>0. 得k2+12k>0. ∴k>0或k<-12.
∴0<k<![]() 或k<-12.
………………………………13分
或k<-12.
………………………………13分
19. 解:(Ι)取 ![]() ,则
,则![]() .
.
取![]() , 得
, 得![]() .
.
故![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列, ∴
的等比数列, ∴![]() =
=![]() .
.
取![]() ,
,![]() ,得
,得![]() =
=![]() +2 (
+2 (![]() ),
),
即![]()
![]() . ∴
. ∴![]() 公差为2的等差数列.
公差为2的等差数列.
又![]() 因此
因此![]()
即![]() ………………………………4分
………………………………4分
(ΙΙ)![]() =
=![]() =
=![]() .
.
∴![]()
=![]()
![]() ,
,
![]()
![]() ,两式相减得,
,两式相减得,
![]()
![]()
![]()
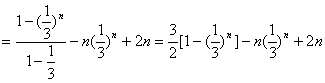 ,
,
∴![]()
![]() .
.
………………………………9分
(ΙΙΙ)![]()
![]() .
.
∴![]()
∴![]() 为增函数,故
为增函数,故![]() .
.
∵![]() ,∴
,∴![]() ,又
,又![]() ,
, ![]() <
<![]() .
.
∴ 1≤![]() <
<![]() .
.
因此,当![]()
![]() 1,且
1,且![]() ≥
≥![]() 时
时 ![]() <
<![]() <
<![]() 恒成立,
恒成立,
∴
存在整数![]() ,
,![]() ,使得对任意正整数
,使得对任意正整数![]() ,不等式
,不等式![]() <
<![]() <
<![]() 恒成立.此时,
恒成立.此时,![]() 的集合是
的集合是![]() ,
,![]() 的集合是
的集合是![]() ,
,
且 ![]() .
………………………………14分
.
………………………………14分
20. 解(Ⅰ)∵ ![]() ,
,
∴ 由![]() ,得
,得![]() ,
,![]() .
.
又![]() ,
,![]() , ∴ 当
, ∴ 当![]() 时,
时,![]() ,
,![]() 递增;
递增;
当![]() 时,
时,![]() ,
,![]() 递减.
递减.
∴ ![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,∴
,∴![]() .
.
又![]() ,
,![]() ,∴
,∴ ![]() .
.
由题意得![]() ,即
,即![]() ,得
,得![]() .
.
故![]() ,
,![]() 为所求. ………………………………5分
为所求. ………………………………5分
(Ⅱ)解:由(1)得![]() ,易知点
,易知点![]() 在曲线
在曲线![]() 上.
上.
又![]() , ∴ 当切点为
, ∴ 当切点为![]() 时,切线
时,切线![]() 的斜率
的斜率![]() ,
,
∴ ![]() 的方程为
的方程为![]() ,即
,即![]() .
.
当切点![]() 不是切点时,设切点为
不是切点时,设切点为![]()
![]() ,切线
,切线![]() 的斜率
的斜率![]() ,
,
∴ ![]() 的方程为
的方程为 ![]() .
.
又点![]() 在
在![]() 上,∴
上,∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,即
,即![]() ,∴
,∴![]() . ∴ 切线
. ∴ 切线![]() 的方程为
的方程为![]() .
.
故所求切线![]() 的方程为
的方程为![]() 或
或![]() . ………………………………9分
. ………………………………9分
( 或者:由(1)知点A(0,1)为极大值点,所以曲线![]() 的点A处的切线为
的点A处的切线为![]() ,恰好经过点
,恰好经过点![]() ,符合题意.)
,符合题意.)
(Ⅲ)解:由已知得![]() ,
,
∴ ![]() .
.
∴ ![]()
![]() .
.
∵![]() ,二次函数
,二次函数![]() 的判别式为
的判别式为
![]() ,
,
整理,得![]() .
.
又![]()
∴当![]() 时,
时,![]() ,此时
,此时![]() ,函数
,函数![]() 为单调递增,极值点个数为0;
为单调递增,极值点个数为0;
当![]() 时,
时,![]() ,此时方程
,此时方程![]() 有两个不相等的实数根,根据极值点的定义,可知函数
有两个不相等的实数根,根据极值点的定义,可知函数![]() 有两个极值点.
………………………………14分
有两个极值点.
………………………………14分
注:2个空的填空题,做对第一个给2分,做对第二个给3分,如有其它解法请阅卷教师酌情给分.
 y 人数
y 人数