高三数学综合模拟
一、 选择题
1．若条件
，条件
，则
是
的txjy
A．必要不充分条件 B．充分不必要条件
C. 充要条件 D. 既不充分也不必要条件
2.三次函数y=f(x)=ax3+x在x∈(－∞,+∞)内是增函数，则
A.a>0 B.a<0
C.a=1 D.a=
3已知
、
表示不同的平面，
、
表示不同的直线，则下列命题中不正确的是
A．若⊥，
，则
B．
，
，则
C．若
，
，则 D．若⊥，⊥，则
4．已知函数
的反函数
，则方程
的解集是txjy
A．{1} B．｛２｝ Ｃ．｛3｝ Ｄ．｛４｝
5．已知
，
，
与
的夹角为
，如果
，
，则
等于txjy
A．
B．
C．
D．
翰林汇66666与双曲线
有共同的渐近线，且经过点A
的双曲线的一个焦点到一条渐近线的距离是
( )
（A）8 （B）4 （C）2 （D）1
7．已知地球球心角1分所对球大圆弧长为1海里．在北纬45°圈上有甲、乙两地，甲地位于东经120°，乙地位于西经150°，则甲、乙两地的球面距离为（ ）．
A．5 400海里 B．7 200海里
C．4 800海里 D．3 600海里
8．设函数
（x
R），若
时，
恒成立，则实数m的取值范围是（ ）
A．（0，1） B．（-∞，0） C．
，
D．，
9．将点
按向量 a平移至点B，若过点B有且只有一条直线l与圆
相切，则当
最小时，直线l的方程是
A．
B．
C．
D．
10．已知函数
，设
，若
≤
，则
A．
B．
C．
D．
二． 填空题
11．已知
, 则
的值为
。
12．在三棱锥
中，
，则二面角
的大小为
．
13已知椭圆
与双曲线
在第一象限内的交点为
，则点到椭圆右焦点的距离等于
。
14．等差数列
中，
，若在每相邻两项间各插入一个数，使之成等差数列，那么新的等差数列的公差是
。
15．P-ABCD是棱长均为a的正四棱锥，则由侧面△
的中心
沿表面走到相对侧面△
的中心
的最短距离等于________．
16．关于函数
，有下列三个命题：
①对于任意
，都有
；
②
在
上是减函数；
③对于任意
，都有
；
其中正确命题的题号是＿＿＿＿＿＿＿＿＿＿＿
三．解答题
17．（本小题满分14分）
已知
、
、
三点的坐标分别为
、
、
，
，
（1）若
，求角的值；
（2）若
，求
的值。
18．（本小题满分14分）
如图，梯形
中，
，
，
是
的中点，将
沿
折起，使点折到点的位置，且二面角
的大小为
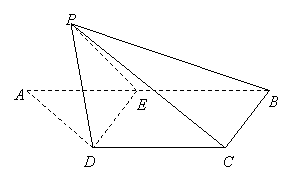（1）求证：
（2）求直线
与平面
所成角的大小
（3）求点
到平面
的距离
19．（本小题满分14分）
已知等差数列的公差
大于0，且
、
是方程
的两根，数列
的前项和为
，且
。
（1）求数列、的通项公式；
（2）设数列的前项和为
，试比较
与
的大小。
20．（本小题满分14分）
已知函数=
，在
处取得极值2。
（1）求函数的解析式；
（2）满足什么条件时，区间
为函数的单调增区间？
（3）若
为=图象上的任意一点，直线
与=的图象切于点，求直线的斜率的取值范围。
21．（本小题满分14分）
对于定义域为D的函数，若同时满足下列条件：
①在D内单调递增或单调递减；
②存在区间[
]
，使在[]上的值域为[]；那么把（
）叫闭函数。
（1）求闭函数
符合条件②的区间[]；
（2）判断函数
是否为闭函数？并说明理由；
（3）若
是闭函数，求实数
的取值范围。