高三数学综合训练试卷（文科）
一、选择题 :（本大题共10小题, 每小题5分, 共50分.）
1、已知集合
，则
的子集的个数（ ）
A. 2个 B. 4个 C. 8个 D. 16个
2． 若函数
的反函数
（ ）
A．1 B．－
3. 已知二个不共线向量
，且
，则一定共线的三是
A. A、B、D B. A、B、C C. B、C、D D. A、C、D （ ）
4．已知
（ ）
A．
B．
C．－
D． 
5．当
时，不等式
恒成立，则实数
的取值范围是（ ） A．（
B．
C．
D．
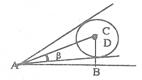6．如图所示，有一广告气球，直径为
时，测得气球的视角
，若
很小时可取
，试估算该气球离地高度BC的值约为
（
）
A．
7．已知椭圆E的短轴长为6，焦点F到长轴的一个端点的距离等于9，则椭圆E的离心率等于 （ ）
A．
B．
C．
D．
8．数列
、
满足
，
，则数列的前10项和为（ ）
A．
B． 
C．
D．
9．将抛物线
沿向量
平移得到抛物线
则向量为（ ）
A．（－1，2） B．（1，－2） C．（－4，2） D．（4，－2）
10.已知函数
为奇函数，函数
为偶函数，且
，则
＝( )
A. 2
B. 
C. 4
D.
二、填空题:（本大题有4小题, 每小题4分, 共16分.）
11．若a、b、c、d均为实数，使不等式
和
都成立的一组值
（a，b，c，d）是
．（只要写出适合条件的一组值即可）
12．已知动圆P与定圆C：
=1相外切，又与定直线L：
相切，那么动圆的圆心P的轨迹方程是
．
13．在条件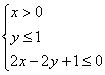
下，目标函数S=2x+y的最大值为
．
14．若曲线
的一条准线方程为
，则
的值是
．
三、解答题 :（本大题有6小题, 共84分. 解答应写出文字说明, 证明过程或演算步骤.）
15．已知
，求
的值．
16．在
中，
．
(Ⅰ)求
的值；
(Ⅱ)当的面积最大时，求
的大小．
17、已知是各项均为正数的等差数列，
成等差数列，又
，
(1)证明：数列是等比数列；
(2)如果数列的前三项和为
，求数列的首项
和公差
。
18.动点P的轨迹是曲线C，且满足：点P到F（－2，0）的距离与它到直线
:x=－4的距离PK之比为常数，又点M（2，
）在曲线C上，点N（－1，1）在曲线C内。
（1）求曲线C的方程；
（2）过
作一条直线交曲线C于
两点，使得
恰好为线段
的中点，求直线的方程。
19.已知
（Ⅰ）若能表示成一个奇函数
和一个偶函数
的和，求和的解析式；
（Ⅱ）若
和
在区间
上都是减函数，求a的取值范围。
20.设
为正整数，规定：
，
已知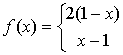
．
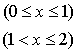（1）解不等式：
（2）设集合
{0，1，2}，对任意
，证明：
；
（3）探求
的值.
参考答案
一、选择题：
DBADB BBCAB
二、填空题：
11．(2,1,-1,-2) 12．
13．2 14．6或86
三、解答题：
15．
．
16．（1）
； （2）
．
17．（1）
； （2）
或
．
18．（1）
；者说 （2）
．
19．（1）
； （2）
．
20．（1）
； （2）略； （3）
．