普通高等学校招生全国统一考试数学分类汇编
第二章《函数》
一、选择题(共40题)
1.(安徽卷)函数![]()
![]() 的反函数是
的反函数是
A.![]()
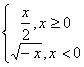 B.
B.![]()
![]() C.
C.![]()
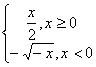 D.
D.![]()
![]()
解:有关分段函数的反函数的求法,选C。也可用特殊点排除法,原函数上有(1,2)和(-1,-1)两点,反函数上有(2,1)和(-1,-1),检验知C。
2.(安徽卷)函数![]() 的反函数是( )
的反函数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
解:由![]() 得:
得:![]() ,所以
,所以![]() 为所求,故选D。
为所求,故选D。
3.(北京卷)已知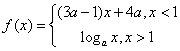 是
是![]() 上的减函数,那么
上的减函数,那么![]() 的取值范围是
的取值范围是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:依题意,有0<a<1且3a-1<0,解得0<a<![]() ,又当x<1时,(3a-1)x+4a>7a-1,当x>1时,logax<0,所以7a-1³0解得x³
,又当x<1时,(3a-1)x+4a>7a-1,当x>1时,logax<0,所以7a-1³0解得x³![]() 故选C
故选C
4.(北京卷)已知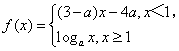 是(-
是(-![]() ,+
,+![]() )上的增函数,那么a的取值范围是
)上的增函数,那么a的取值范围是
(A)(1,+![]() ) (B)(-
) (B)(-![]() ,3) (C)[
,3) (C)[![]() ,3) (D)(1,3)
,3) (D)(1,3)
解:依题意,有a>1且3-a>0,解得1<a<3,又当x<1时,(3-a)x-4a<3-5a,当x³1时,logax³0,所以3-5a£0解得a³![]() ,所以1<a<3故选D
,所以1<a<3故选D
5.(北京卷)在下列四个函数中,满足性质:“对于区间![]() 上的任意
上的任意![]() ,
,![]() 恒成立”的只有
恒成立”的只有
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:![]()
![]()
![]() >1
>1![]() <1\
<1\ ![]() <x1-x2故选A
<x1-x2故选A
6.(福建卷)函数y=㏒![]()
![]() (x﹥1)的反函数是
(x﹥1)的反函数是
A.y=![]() (x>0) B.y=
(x>0) B.y= ![]() (x<0) C.y=
(x<0) C.y=![]() (x>0) D. .y=
(x>0) D. .y=![]() (x<0)
(x<0)
解:对于x>1,函数![]() >0,解得
>0,解得![]() ,
,![]() =
=![]() ,∴ 原函数的反函数是
,∴ 原函数的反函数是![]() ,选A.
,选A.
7.(福建卷)函数![]() 的反函数是
的反函数是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
解:由函数![]() 解得
解得![]() (y≠1),∴ 原函数的反函数是
(y≠1),∴ 原函数的反函数是![]() .
.
8.(福建卷)已知![]() 是周期为2的奇函数,当
是周期为2的奇函数,当![]() 时,
时,![]() 设
设![]()
![]() 则
则
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:已知![]() 是周期为2的奇函数,当
是周期为2的奇函数,当![]() 时,
时,![]() 设
设![]() ,
,![]() ,
,![]() <0,∴
<0,∴![]() ,选D.
,选D.
9.(广东卷)函数![]() 的定义域是
的定义域是
A.![]() B.
B. ![]() C.
C.
![]() D.
D. ![]()
解:由![]() ,故选B.
,故选B.
10.(广东卷)下列函数中,在其定义域内既是奇函数又是减函数的是
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
解:B在其定义域内是奇函数但不是减函数;C在其定义域内既是奇函数又是增函数;D在其定义域内不是奇函数,是减函数;故选A.
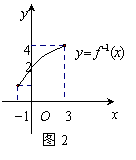 11.(广东卷)函数
11.(广东卷)函数![]() 的反函数
的反函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点
![]() (如图2所示),则方程
(如图2所示),则方程![]() 在
在![]() 上的根是
上的根是![]()
A.4 B.3 C. 2 D.1
解:![]() 的根是
的根是![]() 2,故选C
2,故选C
12.(湖北卷)设![]() ,则
,则![]() 的定义域为
的定义域为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解:f(x)的定义域是(-2,2),故应有-2<![]() <2且-2<
<2且-2<![]() <2解得-4<x<-1或1<x<4
<2解得-4<x<-1或1<x<4
故选B
13.(湖北卷)关于![]() 的方程
的方程![]() ,给出下列四个命题:
,给出下列四个命题:
①存在实数![]() ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数![]() ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数![]() ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数![]() ,使得方程恰有8个不同的实根;
,使得方程恰有8个不同的实根;
其中假命题的个数是
A.0 B.1 C.2 D.3
解:关于x的方程![]() 可化为
可化为![]() …(1)
…(1)
或![]() (-1<x<1)…………(2)
(-1<x<1)…………(2)
①
当k=-2时,方程(1)的解为±![]() ,方程(2)无解,原方程恰有2个不同的实根
,方程(2)无解,原方程恰有2个不同的实根
②
当k=![]() 时,方程(1)有两个不同的实根±
时,方程(1)有两个不同的实根±![]() ,方程(2)有两个不同的实根±
,方程(2)有两个不同的实根±![]() ,即原方程恰有4个不同的实根
,即原方程恰有4个不同的实根
③
当k=0时,方程(1)的解为-1,+1,±![]() ,方程(2)的解为x=0,原方程恰有5个不同的实根
,方程(2)的解为x=0,原方程恰有5个不同的实根
④
当k=![]() 时,方程(1)的解为±
时,方程(1)的解为±![]() ,±
,±![]() ,方程(2)的解为±
,方程(2)的解为±![]() ,±
,±![]() ,即原方程恰有8个不同的实根
,即原方程恰有8个不同的实根
选A
14.(湖南卷)函数![]() 的定义域是( )
的定义域是( )
A.(3,+∞) B.[3, +∞) C.(4, +∞) D.[4, +∞)
解:函数![]() 的定义域是
的定义域是![]() ,解得x≥4,选D.
,解得x≥4,选D.
15.(湖南卷)函数![]() 的定义域是
的定义域是
A.(0,1] B. (0,+∞) C. (1,+∞) D. [1,+∞)
解:函数![]() 的定义域是
的定义域是![]() ,解得x≥1,选D.
,解得x≥1,选D.
16.(江西卷)若不等式x2+ax+1³0对于一切xÎ(0,![]() 〕成立,则a的取值范围是( )
〕成立,则a的取值范围是( )
A.0
B. –2
C.-![]() D.-3
D.-3
解:设f(x)=x2+ax+1,则对称轴为x=![]()
若![]() ³
³![]() ,即a£-1时,则f(x)在〔0,
,即a£-1时,则f(x)在〔0,![]() 〕上是减函数,应有f(
〕上是减函数,应有f(![]() )³0Þ
)³0Þ
-![]() £x£-1
£x£-1
若![]() £0,即a³0时,则f(x)在〔0,
£0,即a³0时,则f(x)在〔0,![]() 〕上是增函数,应有f(0)=1>0恒成立,故a³0
〕上是增函数,应有f(0)=1>0恒成立,故a³0
若0£![]() £
£![]() ,即-1£a£0,则应有f(
,即-1£a£0,则应有f(![]() )=
)=![]() 恒成立,故-1£a£0
恒成立,故-1£a£0
综上,有-![]() £a故选C
£a故选C
17.(江西卷)某地一年的气温Q(t)(单位:ºc)与时间t(月份)之间的关系如图(1)示,已知该年的平均气温为10ºc,令G(t)表示时间段〔0,t〕的平均气温,G(t)与t之间的函数关系用下列图象表示,则正确的应该是( )

|
解:结合平均数的定义用排除法求解A
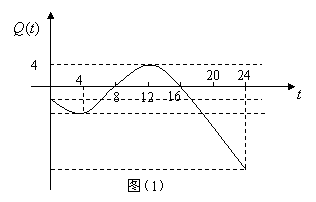
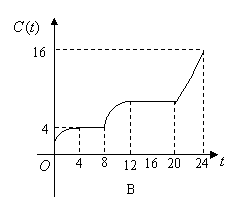
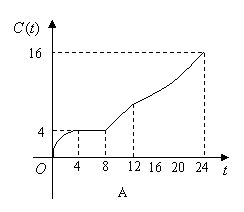 18.(江西卷)某地一天内的气温
18.(江西卷)某地一天内的气温![]() (单位:℃)与时刻
(单位:℃)与时刻![]() (单位:时)之间的关系如图(1)所示,令
(单位:时)之间的关系如图(1)所示,令![]() 表示时间段
表示时间段![]() 内的温差(即时间段
内的温差(即时间段![]() 内最高温度与最低温度的差).
内最高温度与最低温度的差).![]() 与
与![]() 之间的函数关系用下列图象表示,则正确的图象大致是( )
之间的函数关系用下列图象表示,则正确的图象大致是( )
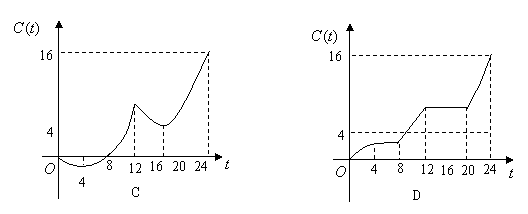 |
解:结合图象及函数的意义可得D。
19.(辽宁卷)设![]() 是R上的任意函数,则下列叙述正确的是
是R上的任意函数,则下列叙述正确的是
(A)![]() 是奇函数 (B)
是奇函数 (B)![]() 是奇函数
是奇函数
(C) ![]() 是偶函数 (D)
是偶函数 (D) ![]() 是偶函数
是偶函数
【解析】A中![]() 则
则![]() ,
,
即函数![]() 为偶函数,B中
为偶函数,B中![]() ,
,![]() 此时
此时![]() 与
与![]() 的关系不能确定,即函数
的关系不能确定,即函数![]() 的奇偶性不确定,
的奇偶性不确定,
C中![]() ,
,![]() ,即函数
,即函数![]() 为奇函数,D中
为奇函数,D中![]() ,
,![]() ,即函数
,即函数![]() 为偶函数,故选择答案D。
为偶函数,故选择答案D。
【点评】本题考查了函数的定义和函数的奇偶性的判断,同时考查了函数的运算。
20.(辽宁卷)与方程![]() 的曲线关于直线
的曲线关于直线![]() 对称的曲线的方程为
对称的曲线的方程为
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
解:![]() ,
,![]() ,即:
,即:![]() ,所以
,所以![]() ,故选择答案A。
,故选择答案A。
21.(全国卷I)已知函数![]() 的图象与函数
的图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则
A.![]() B.
B.![]()
C.![]() D.
D.![]()
解:函数![]() 的图象与函数
的图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称,所以
对称,所以![]() 是
是![]() 的反函数,即
的反函数,即![]() =
=![]() ,∴
,∴ ![]() ,选D.
,选D.
22.(全国II)函数y=lnx-1(x>0)的反函数为
(A)y=ex+1(x∈R) (B)y=ex-1(x∈R) (C)y=ex+1(x>1) (D)y=ex-1(x>1)
解析:![]() 所以反函数为
所以反函数为![]() 故选B
故选B
23.(全国II)函数y=f(x)的图像与函数g(x)=log2x(x>0)的图像关于原点对称,则f(x)的表达式为
(A)f(x)=(x>0) (B)f(x)=log2(-x)(x<0)
(C)f(x)=-log2x(x>0) (D)f(x)=-log2(-x)(x<0)
解析:(x,y)关于原点的对称点为(-x,-y),所以![]()
![]()
![]() 选D
选D
本题主要考察对称的性质和对数的相关性质,比较简单,但是容易把![]() 与
与![]() 搞混,其实
搞混,其实![]()
24.(全国II)如果函数![]() 的图像与函数
的图像与函数![]() 的图像关于坐标原点对称,则
的图像关于坐标原点对称,则![]() 的表达式为
的表达式为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:以-y,-x代替函数![]() 中的x,
中的x,![]() ,得
,得 ![]() 的表达式为
的表达式为![]()
,选D
25.(全国II)函数f(x)=的最小值为
(A)190 (B)171 (C)90 (D)45
解析:![]() 表示数轴上一点到1,2,3…19的距离之和,可知x在1—19最中间时f(x)取最小值.即x=10时f(x)有最小值90,故选C
表示数轴上一点到1,2,3…19的距离之和,可知x在1—19最中间时f(x)取最小值.即x=10时f(x)有最小值90,故选C
本题主要考察求和符号的意义和绝对值的几何意义,难度稍大,且求和符号不在高中要求范围内,只在线性回归中简单提到过.
26.(山东卷)函数y=1+ax(0<a<1)的反函数的图象大致是
 |
(A) (B) (C) (D)
解:函数y=1+ax(0<a<1)的反函数为![]() ,它的图象是函数
,它的图象是函数![]() 向右移动1个单位得到,选A
向右移动1个单位得到,选A
27.(山东卷)已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),则,f(6)的值为
(A)-1 (B) 0 (C) 1 (D)2
解:因为f(x)是定义在R上的奇函数,所以f(0)=0,又f(x+4)=-f(x+2)=f(x),故函数,f(x)的周期为4,所以f(6)=f(2)=-f(0)=0,选B
28.(山东卷)设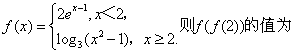
(A)0 (B)1 (C)2 (D)3
解:f(f(2))=f(1)=2,选C
29.(陕西卷)设函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(2,1),其反函数的图像过点(2,8),则a+b等于( )
A.6 B.5 C.4 D.3
解析:函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(2,1),其反函数的图象过点(2,8),
则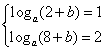 ,∴
,∴![]() ,
,![]() 或
或![]() (舍),b=1,∴a+b=4,选C.
(舍),b=1,∴a+b=4,选C.
30.(陕西卷)函数f(x)= (x∈R)的值域是( )
A.(0,1) B.(0,1] C.[0,1) D.[0,1]
解析:函数f(x)= (x∈R),∴ ![]() 1,所以原函数的值域是(0,1]
,选B.
1,所以原函数的值域是(0,1]
,选B.
31.(陕西卷)设函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(0, 0),其反函数的图像过点(1,2),则a+b等于( )
A.6 B.5 C.4 D.3
解析:函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(0,0),其反函数的图象过点(1,2),
则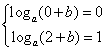 ,∴
,∴![]() ,a=3,则a+b等于4,选C.
,a=3,则a+b等于4,选C.
32.(四川卷)函数![]() 的反函数是
的反函数是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
解析:函数![]() ,解得
,解得![]() (y∈R),所以原函数的反函数是
(y∈R),所以原函数的反函数是![]() ,选A.
,选A.
33.(天津卷)已知函数![]() 的图象与函数
的图象与函数![]() (
(![]() 且
且![]() )的图象关于直线
)的图象关于直线![]() 对称,记
对称,记![]() .若
.若![]() 在区间
在区间![]() 上是增函数,则实数
上是增函数,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解析:已知函数![]() 的图象与函数
的图象与函数![]() (
(![]() 且
且![]() )的图象关于直线
)的图象关于直线![]() 对称,则
对称,则![]() ,记
,记![]() =
=![]() .当a>1时,若
.当a>1时,若![]() 在区间
在区间![]() 上是增函数,
上是增函数,![]() 为增函数,令
为增函数,令![]() ,t∈[
,t∈[![]() ,
, ![]() ],要求对称轴
],要求对称轴![]() ,矛盾;当0<a<1时,若
,矛盾;当0<a<1时,若![]() 在区间
在区间![]() 上是增函数,
上是增函数,![]() 为减函数,令
为减函数,令![]() ,t∈[
,t∈[![]() ,
,![]() ],要求对称轴
],要求对称轴![]() ,解得
,解得![]() ,所以实数
,所以实数![]() 的取值范围是
的取值范围是![]() ,选D.
,选D.
34.(天津卷)设![]() ,
,![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解析:![]() 则
则![]() ,选A.
,选A.
35.(天津卷)函数![]() 的反函数是( )
的反函数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
解析:由函数![]() 解得
解得![]() (y>2),所以原函数的反函数是
(y>2),所以原函数的反函数是![]() ,选D.
,选D.
36.(天津卷)如果函数![]() 在区间
在区间![]() 上是增函数,那么实数
上是增函数,那么实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.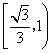 C.
C.![]() D.
D.![]()
解析:函数y![]() 且
且![]() 可以看作是关于
可以看作是关于![]() 的二次函数,若a>1,则
的二次函数,若a>1,则![]() 是增函数,原函数在区间
是增函数,原函数在区间![]() 上是增函数,则要求对称轴
上是增函数,则要求对称轴![]() ≤0,矛盾;若0<a<1,则
≤0,矛盾;若0<a<1,则![]() 是减函数,原函数在区间
是减函数,原函数在区间![]() 上是增函数,则要求当
上是增函数,则要求当![]() (0<t<1)时,
(0<t<1)时,![]() 在t∈(0,1)上为减函数,即对称轴
在t∈(0,1)上为减函数,即对称轴![]() ≥1,∴
≥1,∴![]() ,∴实数
,∴实数![]() 的取值范围是
的取值范围是![]() ,选B.
,选B.
37.(浙江卷))已知![]() ,则
,则
(A)1<n<m (B) 1<m<n (C)m<n<1 (D) n<m<1
【考点分析】本题考查对数函数的性质,基础题。
解析:由![]() 知函数
知函数![]() 为减函数,由
为减函数,由![]() 得
得
![]() ,故选择A。
,故选择A。
38.(浙江卷)对a,b![]() R,记max{a,b}=
R,记max{a,b}=![]() ,函数f(x)=max{x+1,x-2}(x
,函数f(x)=max{x+1,x-2}(x![]() R)的最小值是
R)的最小值是
(A)0
(B)![]() (C)
(C) ![]() (D)3
(D)3
解:当x<-1时,x+1=-x-1,x-2=2-x,因为(-x-1)-(2-x)=-3<0,所以2-x>-x-1;当-1£x<![]() 时,x+1=x+1,x-2=2-x,因为(x+1)-(2-x)=2x-1<0,x+1<2-x;当
时,x+1=x+1,x-2=2-x,因为(x+1)-(2-x)=2x-1<0,x+1<2-x;当![]() £x<2时,x+1³2-x;当x³2时,x+1=x+1,x-2=x-2,显然x+1>x-2;
£x<2时,x+1³2-x;当x³2时,x+1=x+1,x-2=x-2,显然x+1>x-2;
故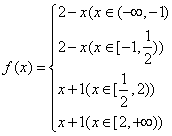 据此求得最小值为
据此求得最小值为![]() 。选C
。选C
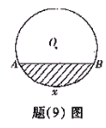 39.(重庆卷)如图所示,单位圆中弧AB的长为x,f(x)表示弧AB与弦AB所围成的弓形面积的2倍,则函数y=f(x)的图象是
39.(重庆卷)如图所示,单位圆中弧AB的长为x,f(x)表示弧AB与弦AB所围成的弓形面积的2倍,则函数y=f(x)的图象是
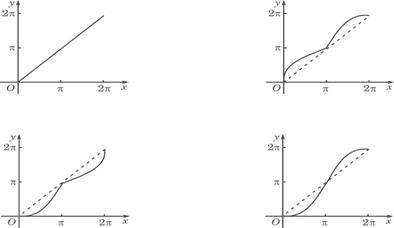
解析:如图所示,单位圆中![]() 的长为
的长为![]() ,
,![]()
![]() 与弦AB所围成的弓形面积的2倍,当
与弦AB所围成的弓形面积的2倍,当![]() 的长小于半圆时,函数
的长小于半圆时,函数![]() 的值增加的越来越快,当
的值增加的越来越快,当![]() 的长大于半圆时,函数
的长大于半圆时,函数![]() 的值增加的越来越慢,所以函数
的值增加的越来越慢,所以函数![]() 的图像是D.
的图像是D.
40.(重庆卷)设函数![]() 的反函数为
的反函数为![]() ,且
,且![]() 的图像过点
的图像过点![]() ,则
,则![]() 的图像必过
的图像必过
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:当x=![]() 时,2x-1=0,即y=f(x)的图象过点(0,1),所以
时,2x-1=0,即y=f(x)的图象过点(0,1),所以![]() 的图像必过(1,0)故选C。
的图像必过(1,0)故选C。
二、填空题(共14题)
41.(安徽卷)函数![]() 对于任意实数
对于任意实数![]() 满足条件
满足条件![]() ,若
,若![]() 则
则![]() _______________。
_______________。
解:由![]() 得
得![]() ,所以
,所以![]() ,则
,则![]() 。
。
42.(北京卷)已知函数![]() 的反函数的图象经过点(-1,2),那么a的值等于
.
的反函数的图象经过点(-1,2),那么a的值等于
.
解:依题意,当x=2时,y=1,代入![]() 中,得a=2
中,得a=2
43.(江西卷)设f(x)=log3(x+6)的反函数为f-1(x),若〔f-1(m)+6〕〔f-1(n)+6〕=27,则f(m+n)=___________________
解:f-1(x)=3x-6故〔f-1(m)+6〕·〔f-1(x)+6〕=3m·3n=3m +n=27
\m+n=3\f(m+n)=log3(3+6)=2。
44.(辽宁卷)设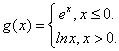 则
则![]() __________
__________
【解析】![]() .
.
【点评】本题考察了分段函数的表达式、指对数的运算.
45.(辽宁卷)方程![]() 的解为 .
的解为 .
解:![]() Û
Û![]() ,即
,即![]() 解得
解得![]() (负值舍去),所以
(负值舍去),所以![]() 。
。
46.(全国卷I)已知函数![]() ,若
,若![]() 为奇函数,则
为奇函数,则![]() ________。
________。
解析:函数![]() 若
若![]() 为奇函数,则
为奇函数,则![]() ,即
,即![]() ,a=
,a=![]() .
.
47.(上海卷)若函数![]() =
=![]() (
(![]() >0,且
>0,且![]() ≠1)的反函数的图像过点(2,-1),则
≠1)的反函数的图像过点(2,-1),则![]() = .
= .
解:由互为反函数关系知,![]() 过点
过点![]() ,代入得:
,代入得:![]() ;
;
48.(上海卷)方程![]() 的解是_______.
的解是_______.
解:方程![]() 的解满足
的解满足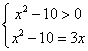 ,解得x=5.
,解得x=5.
49.(浙江卷)对a,b![]() R,记maxa,b=
R,记maxa,b=![]() 函数f(x)=maxx+1,x-2(x
函数f(x)=maxx+1,x-2(x![]() R)的最小值是 .
R)的最小值是 .
【考点分析】本题考查新定义函数的理解、解绝对值不等式,中档题。
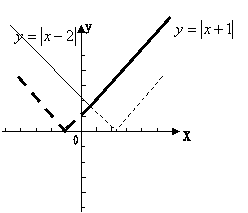 解析:由
解析:由![]() ,故
,故
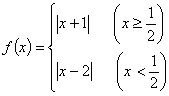 ,其图象如右,
,其图象如右,
则![]() 。
。
【名师点拔】数学中考查创新思维,要求必须要有良好的数学素养。
50.(重庆卷)设![]() ,函数
,函数![]() 有最大值,则不等式
有最大值,则不等式![]() 的解集为
。
的解集为
。
解析:设![]() ,函数
,函数![]() 有最大值,∵
有最大值,∵![]() 有最小值,∴ 0<a<1, 则不等式
有最小值,∴ 0<a<1, 则不等式![]() 的解为
的解为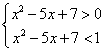 ,解得2<x<3,所以不等式的解集为
,解得2<x<3,所以不等式的解集为![]() .
.
51.(重庆卷)设![]() ,函数
,函数![]() 有最小值,则不等式
有最小值,则不等式![]() 的解集为
。
的解集为
。
解:由![]() ,函数
,函数![]() 有最小值可知a>1,所以不等式
有最小值可知a>1,所以不等式![]() 可化为x-1>1,即x>2.
可化为x-1>1,即x>2.
52.(上海春)方程![]() 的解
的解![]() .
.
解:由log3(2x-1),化为同底数的对数,得log3(2x-1)=log33,2x-1=3 ,即 x=2 .从而应填2.
53.(上海春)函数![]() 的反函数
的反函数![]() .
.
解:先求原函数的值域,再反解.由y=3x+5,x∈[0,1] ,得y∈[5,8] .解出 ![]() ,从而
,从而 ![]() ,x∈[5,8]
. 从而应填
,x∈[5,8]
. 从而应填 ![]() .
.
54.(上海春)已知函数![]() 是定义在
是定义在![]() 上的偶函数. 当
上的偶函数. 当![]() 时,
时,![]() ,则 当
,则 当![]() 时,
时,![]() .
.
解:当x∈(0,+∞) 时,有-x∈(-∞,0),注意到函数f(x) 是定义在
(-∞,+∞)上的偶函数,于是,有f(x)=f(-x)=-x-(-x)4=-x-x4
.从而应填-x-x4.
三、解答题(共6题)
55.(广东卷)![]() 是定义在
是定义在![]() 上且满足如下条件的函数
上且满足如下条件的函数![]() 组成的集合:①对任意的
组成的集合:①对任意的![]() ,都有
,都有![]() ;②存在常数
;②存在常数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() .
.
(I)设![]() ,证明:
,证明:![]()
(II)设![]() ,如果存在
,如果存在![]() ,使得
,使得![]() ,那么这样的
,那么这样的![]() 是唯一的;
是唯一的;
(III)
设![]() ,任取
,任取![]() ,令
,令![]() ,
,![]() ,证明:给定正整数
,证明:给定正整数![]() ,对任意的正整数
,对任意的正整数![]() ,成立不等式
,成立不等式![]()
解:(I)对任意![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,所以
,所以![]() ,
,
对任意的![]() ,
,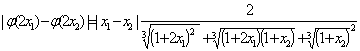 ,
,
![]()
![]() ,所以0<
,所以0<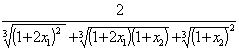
![]() ,令
,令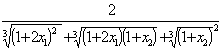 =
=![]() ,
,![]() ,
,![]()
所以![]()
(II)反证法:设存在两个![]() 使得
使得![]() ,
,![]() 则
则
由![]() ,得
,得![]() ,所以
,所以![]() ,矛盾,故结论成立。
,矛盾,故结论成立。
(III)
![]() ,所以
,所以![]()
![]()
![]()
![]()
![]() +…
+…
![]()
![]()
56.(江苏卷)设a为实数,设函数![]() 的最大值为g(a)。
的最大值为g(a)。
(Ⅰ)设t=![]() ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)
(Ⅲ)试求满足![]() 的所有实数a
的所有实数a
解析:本小题主要考查函数、方程等基本知识,考查分类讨论的数学思想方法和综合运用数学知识分析问题、解决问题的能力。
(Ⅰ)令![]()
要使有t意义,必须1+x≥0且1-x≥0,即-1≤x≤1,
∴![]() t≥0
①
t≥0
①
t的取值范围是![]() 由①得
由①得![]()
∴m(t)=a(![]() )+t=
)+t=![]()
(Ⅱ)由题意知g(a)即为函数![]() 的最大值。
的最大值。
注意到直线![]() 是抛物线
是抛物线![]() 的对称轴,分以下几种情况讨论。
的对称轴,分以下几种情况讨论。
(1)当a>0时,函数y=m(t), ![]() 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由![]() <0知m(t)在
<0知m(t)在![]() 上单调递增,∴g(a)=m(2)=a+2
上单调递增,∴g(a)=m(2)=a+2
(2)当a=0时,m(t)=t, ![]() ,∴g(a)=2.
,∴g(a)=2.
(3)当a<0时,函数y=m(t), ![]() 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若![]() ,即
,即![]() 则
则![]()
若![]() ,即
,即![]() 则
则![]()
若![]() ,即
,即![]() 则
则![]()
综上有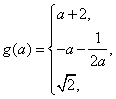
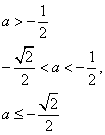
(III)解法一:
情形1:当![]() 时
时![]() ,此时
,此时![]() ,
,![]()
由![]() ,与a<-2矛盾。
,与a<-2矛盾。
情形2:当![]()
![]() 时,此时
时,此时![]() ,
,![]()
![]() 解得,
解得, ![]() 与
与![]() 矛盾。
矛盾。
情形3:当![]()
![]() 时,此时
时,此时![]()
所以![]()
情形4:当![]() 时,
时,![]() ,此时
,此时![]() ,
,
![]()
![]() 矛盾。
矛盾。
情形5:当![]() 时,
时,![]() ,此时g(a)=a+2,
,此时g(a)=a+2, ![]()
由![]() 解得
解得![]() 矛盾。
矛盾。
情形6:当a>0时,![]() ,此时g(a)=a+2,
,此时g(a)=a+2, ![]()
由![]() ,由a>0得a=1.
,由a>0得a=1.
综上知,满足![]() 的所有实数a为
的所有实数a为![]() 或a=1
或a=1
57.(浙江卷)设f(x)=3ax![]() ,f(0)>0,f(1)>0,求证:
,f(0)>0,f(1)>0,求证:
(Ⅰ)a>0且-2<![]() <-1;
<-1;
(Ⅱ)方程f(x)=0在(0,1)内有两个实根.
解析:本题主要考查二次函数的基本性质与不等式的应用等基础知识。满分14分。
证明:(I)因为![]() ,所以
,所以![]() .
.
由条件![]() ,消去
,消去![]() ,得
,得![]() ;
;
由条件![]() ,消去
,消去![]() ,得
,得![]() ,
,![]() .
.
故![]() .
.
(II)抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,
,
在![]() 的两边乘以
的两边乘以![]() ,得
,得![]() .
.
又因为![]() 而
而![]()
所以方程![]() 在区间
在区间![]() 与
与![]() 内分别有一实根。
内分别有一实根。
故方程![]() 在
在![]() 内有两个实根.
内有两个实根.
58.(重庆卷) 已知定义域为R的函数![]() 满足
满足![]()
(I)若![]() ,求
,求![]() ;又若
;又若![]() ,求
,求![]() ;
;
(II)设有且仅有一个实数![]() ,使得
,使得![]() ,求函数
,求函数![]() 的解析表达式
的解析表达式
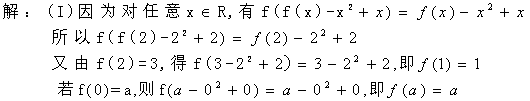
 59.(重庆卷)已知定义域为
59.(重庆卷)已知定义域为![]() 的函数
的函数![]() 是奇函数。
是奇函数。
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若对任意的![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
解析:(Ⅰ)因为![]() 是奇函数,所以
是奇函数,所以![]() =0,即
=0,即![]()
又由f(1)= -f(-1)知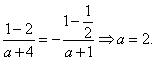
(Ⅱ)解法一:由(Ⅰ)知![]() ,易知
,易知![]() 在
在![]() 上
上
为减函数。又因![]() 是奇函数,从而不等式:
是奇函数,从而不等式: ![]()
等价于![]() ,因
,因![]() 为减函数,由上式推得:
为减函数,由上式推得:
![]() .即对一切
.即对一切![]() 有:
有:![]() ,
,
从而判别式![]()
解法二:由(Ⅰ)知![]() .又由题设条件得:
.又由题设条件得: ![]() ,
,
即 :![]() ,
,
整理得 ![]()
![]()
上式对一切![]() 均成立,从而判别式
均成立,从而判别式![]()
60.(上海春) 设函数![]() .
.
(1)在区间![]() 上画出函数
上画出函数![]() 的图像;
的图像;
(2)设集合![]() . 试判断集合
. 试判断集合![]() 和
和![]() 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当![]() 时,求证:在区间
时,求证:在区间![]() 上,
上,![]() 的图像位于函数
的图像位于函数![]() 图像的上方.
图像的上方.
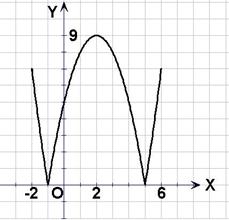 解:(1)
解:(1)
(2)方程![]() 的解分别是
的解分别是![]() 和
和![]() ,由于
,由于![]() 在
在![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 和
和![]() 上单调递增,因此
上单调递增,因此
![]() .
.
由于![]() .
.
(3)[解法一] 当![]() 时,
时,![]() .
.
![]()
![]()
![]() ,
,
![]()
![]() . 又
. 又![]() ,
,
①
当![]() ,即
,即![]() 时,取
时,取![]() ,
,
![]()
![]() .
.
![]() ,
,
则![]() .
.
②
当![]() ,即
,即![]() 时,取
时,取![]() ,
, ![]() =
=![]() .
.
由 ①、②可知,当![]() 时,
时,![]() ,
,![]() .
.
因此,在区间![]() 上,
上,![]() 的图像位于函数
的图像位于函数![]() 图像的上方.
图像的上方.
[解法二] 当![]() 时,
时,![]() .
.
由![]() 得
得![]() ,
,
令 ![]() ,解得
,解得 ![]() 或
或![]() ,
,
在区间![]() 上,当
上,当![]() 时,
时,![]() 的图像与函数
的图像与函数![]() 的图像只交于一点
的图像只交于一点![]() ; 当
; 当![]() 时,
时,![]() 的图像与函数
的图像与函数![]() 的图像没有交点.
的图像没有交点.
如图可知,由于直线![]() 过点
过点![]() ,当
,当![]() 时,直线
时,直线![]() 是由直线
是由直线![]() 绕点
绕点![]() 逆时针方向旋转得到. 因此,在区间
逆时针方向旋转得到. 因此,在区间![]() 上,
上,![]() 的图像位于函数
的图像位于函数![]() 图像的上方.
图像的上方.