集合的概念和运算

基础训练1　集合的概念和运算

●训练指要

理解集合、全集、空集、子集、交集、并集、补集等概念；正确表达元素与集合，集合与集合之间的关系，掌握集合的表示法和集合的交、并、补等运算.

一、选择题

1.(2003年安徽春季高考题)集合S={a,b,c,d,e},包含{a,b}的S的子集共有

A.2个　　　　　　　　　　　　　B.3个　　　　　　　　　　　　　C.5个　　　　　　　　　 D.8个

2.(2002年全国高考题)设集合M={xx=,k∈Z},N={xx=,k∈Z},则

A.M=N　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.MN

C.MN　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.M∩N=

3.六个关系式

①{(a,b)}={(b,a)}　②{a,b}={b,a}　③{0}　④0∈{0}  ⑤∈{0}　⑥={0}

其中正确的个数为

A.6　　　　　　　　　　　　　　　B.5　　　　　　　　　　　　　　　C.4　　　　　　　　　　　 D.3

二、填空题

4.设全集U={xx≤20,x∈N^*},集合P={能被2或3整除的自然数}，用列举法表示集合

_UP=_________.

5.设方程x²-px-q=0的解集为A，方程x²+qx-p=0的解集为B，若A∩B={1}，则p+q=_________.

三、解答题

6.已知集合M={a,a+m,a+2m},N={a,an,an²},如果M=N，求n的值.

7.已知全集U={xx²-3x+2≥0},A={xx-2>1},B={x≥0},求_UA、_UB、A∩B、A∪B、(_UA)∪B，A∩(_UB).

8.已知集合A={-1，2}，B={xmx+1=0},若A∪B=A，求实数m的取值集合M.

基础训练4　映射与函数、反函数

●训练指要

了解映射与函数的概念；熟练掌握反函数的求法.

一、选择题

1.从集合A={a,b}到集合B={x,y}可以建立的映射有

A.1个　　　　　　　　　　　　　B.2个　　　　　　　　　 C.3个　　　　　　　　　 D.4个

2.(2000年全国高考题)设A、B都是自正整数集N^*，映射f:A→B把集合A中的元素n映射到集合B中的元素2ⁿ+n.则在映射f下，象20的原象是

A.2　　　　　　　　　　　　　　　B.3　　　　　　　　　　　 C.4　　　　　　　　　　　 D.5

3.(1999年全国高考题)已知映射f:A→B.其中，集合A={-3，-2，-1，1，2，3，4}，集合B中的元素都是A中元素在映射f下的象.且对任意的a∈A,在B中和它对应的元素是a,则集合B中元素的个数是

A.4　　　　　　　　　　　　　　　B.5　　　　　　　　　　　 C.6　　　　　　　　　　　 D.7

二、填空题

4.(2003年上海春季高考题)已知函数f(x)= +1,则f ^-1(3)=_________.

5.设f:A→B是从A到B的映射，其中A=B={(x,y)x,y∈R},f:(x,y)→(x+y,x-y),那么A中元素(1，3)的象是_________，B中元素(1，3)的原象是_________.

三、解答题

6.(2001年北京春季高考题)求函数y=- (x≤1)的反函数f ^-1(x).

7.求下列函数的反函数.

(1)y=x²-2x+3(x>1)　　 (2)y=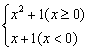

8.动点P从边长为1的正方形ABCD的顶点A出发顺次经过B、C、D，再回到A；设x表示P的行程，y表示PA的长，求y关于x的函数.

基础训练5  函数的定义域、值域及解析式求法

●训练指要

确定函数解析式的方法，掌握根据函数解析式和实际问题的函数式的定义域的计算.

一、选择题

1.函数y=的定义域是

A.-1≤x≤1　　　　　　　　　　　　　　　　　　　　　　　 B.x≥1或x≤-1

C.0≤x≤1　　　　　　　　　　　　　　　　　　　　　　　　D.{-1,1}

2.(2001年北京春季高考题)已知f(x⁶)=log₂x，那么f(8)等于

A.　　　　　　　　　　　　　　B.8　　　　　　　　　　　 C.18　　　　　　　　　　　　　　D.

3.已知函数f(x)的定义域是［0，1］，则函数f(x+a)+f(x-a)(其中0<a<)的定义域是

A.　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.［a,1-a］

C.［-a,1+a］　　　　　　　　　　　　　　　　　　　　　 D.［0,1］

二、填空题

4.(2002年上海春季高考题)函数y=的定义域为_________.

5.(2002年全国高考题)已知函数f(x)=,那么f(1)+f(2)+

=_________.

三、解答题

6.已知f(+1)=x+2,求f(x)的表达式.

7.求下列函数的定义域.

(1)y=+lg(10-x);(2)y=+lgcosx;

(3)已知y=f(2^x)的定义域为［-1，1］，求y=f(log₂x)的定义域.

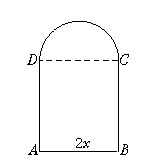
8.周长为l的铁丝弯成下部为矩形，上部为半圆形的框架，若矩形底边上为2x,求此框架围成图形的面积y与x的函数式y=f(x),并写出它的定义域.

基础训练6  函数的奇偶性、单调性、对称性

理解函数奇偶性、单调性的概念；掌握函数奇偶性、单调性的判定方法.

一、选择题

1.下列判断正确的是

A.f(x)=是奇函数　　　B.f(x)=(1-x)是偶函数

C.f(x)=lg(x+)是非奇非偶函数　　D.f(x)=1既是奇函数又是偶函数

2.(2001年全国高考题)设f(x)、g(x)都是单调函数，有如下命题：

①若f(x)单调递增，g(x)单调递增，则f(x)-g(x)单调递增；

②若f(x)单调递增，g(x)单调递减，则f(x)-g(x)单调递增；

③若f(x)单调递减，g(x)单调递增，则f(x)-g(x)单调递减；

④若f(x)单调递减，g(x)单调递减，则f(x)-g(x)单调递减.

其中正确的命题是

A.①③　　　　　　　　　　　　 B.①④　　　　　　　　　　　　 C.②③　　　　　　　　　　　　 D.②④

3.已知f(x)是定义在R上的奇函数，当x<0时，f(x)=()^x,那么f()的值是

A. 　　　　　　　　　　　 B.-　　　　　　　　　　　　C.　　　　　　　　　　　　　D.-

二、填空题

4.函数y=(x²-6x+8)的单调递增区间是_________；单调递减区间是_________.

5.(2002年天津试题)设函数f(x)在(-∞,+∞)内有定义，下列函数①y=-f(x)　②y=xf(x²)　③y=-f(-x)　④y=f(x)-f(-x)中必为奇函数的有_________.(要求填写正确答案的序号)

三、解答题

6.函数f(x)对任意m、n∈R,都有f(m+n)=f(m)+f(n)-1,并且当x>0时，f(x)>1.

(1)求证f(x)是R上的增函数.

(2)设f(3)=4,解不等式f(a²+a-5)<2.

7.讨论函数f(x)=x+及g(x)=x-的单调性.

8.(2003年上海春季高考题)已知函数f(x)=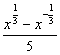,g(x)= .

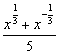(1)证明f(x)是奇函数，并求f(x)的单调区间.

(2)分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值.由此概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式，并加以证明.

基础训练7　二次函数与二次方程

●训练指要

掌握二次函数的图象和性质；掌握二次函数在闭区间上的最值.

一、选择题

1.已知二次函数y=ax²+bx+c的图象的顶点坐标为(2，-1)，与y轴的交点为(0，11)，则

A.a=1,b=-4,c=11　　　　　　　　　　　　　　　　　　　 B.a=3,b=12,c=11

C.a=3,b=-6,c=11　　　　　　　　　　　　　　　　　　　 D.a=3,b=-12,c=11

2.已知f(x)=(m-1)x²-2mx+3是偶函数，则在(-∞,3)内此函数

A.是增函数  　　　　　　　　　　　　　　　　　　　　　　　　 B.不是单调函数

C.是减函数　　　　　　　　　　　　　　　　　　　　　　　D.不能确定

3.如果函数y=x²+ax-1在区间［0，3］上有最小值-2，那么实数a的值为

A.2　　　　　　　　　　　B.±2　　　　　　　　　　　　　 C.-2　　　　　　　　　　　D.-

二、填空题

4.(2003年上海春季高考题)若函数y=x²+(a+2)x+3,x∈［a,b］的图象关于直线x=1对称，则b=_________.

5.已知［1，3］是函数y=-x²+4ax的单调递减区间，则实数a的取值范围是_________.

三、解答题

6.已知二次函数y=ax²+bx+c(a>0)的图象与两坐标轴交点分别为(-1，0)和(0，-1)，且顶点在y轴的右侧，求b的取值范围.

7.求函数f(x)=x²+2x+1在区间［t,t+1］上的最小值g(t),并求出g(t)的最小值.

8.对于x∈R,二次函数f(x)=x²-4ax+2a+30(a∈R)的值均为非负数，求关于x的方程=a-1+1的根的范围.

基础训练8　指数式、对数式及函数图象变换

●训练指要

熟悉指数式、对数式的运算及变换.

一、选择题

1.的值是

A.　　　　　　　　　　　　　　B.1　　　　　　　　　　　C.　　　　　　D.2

2.三个数6^0.7,0.7⁶,log_0.76的大小顺序是

A.0.7⁶<log_0.76<6^0.7 B.0.7⁶<6^0.7<log_0.76

C.log_0.76<6^0.7<0.7⁶ D.log_0.76<0.7⁶<6^0.7

3.设a、b、c均为正数，且3^a=4^b=6^c,那么

A.　　　　　　　　　　　　　　　　　　　　B.

C.　　　　　　　　　　　　　　　　　　　　　　D.

二、填空题

4.(log₂3+log₄9+log₈27+…+3ⁿ)·log₉=_________.

5.(log₄3+log₈3)(log₃2+log₉8)=_________.

三、解答题

6.给出函数f(x)=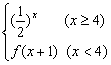求f(log₂3)的值.

7.已知10^a=12,10^b=14,10^c=18,求lg42,(用a、b、c的代数式表示).

8.已知常数a>1,变数x、y之间有关系式log_ax+3log_xa-log_xy=3.

(1)若x=a^t,试求以a、t表示y的表达式；

(2)若t∈［1,+∞时，y的最小值是8，求a和x的值.

基础训练9　函数最值及应用

●训练指要

掌握求最值常见的方法：配方法、判别式法、单调性法、不等式法、换元法、数形结合法等.

一、选择题

1.(2003年北京春季高考题)函数f(x)=的最大值是

A.　　　　　　　　　　　　　　B.　　　　　　C.　　　　　　　　　　 D.

2.函数y=x²-2x+3在闭区间［0，m］上有最大值3，最小值2，则m的取值范围是

A.(-∞,2　　　　　　　　　　　　　　B.［0,2］　　　　　　　C.［1,2］　　　　　　 D.［1,+∞)

3.如果实数x、y满足等式(x-2)²+y²=3,那么的最大值是

A.　　　　　　　　　　　　　　B. 　　　　　　　　 C.　　　　　　　　　D.

二、填空题

4.(2002年全国高考题)函数y=a^x在［0，1］上的最大值与最小值的和为3，则a=_________.

5.函数y=的最大值为_________，最小值为_________.

三、解答题

6.已知-1≤x≤0,求函数f(x)=2^x+2-3·4^x的最大值和最小值.

7.(2000年北京春季高考题)已知二次函数f(x)=(lga)x²+2x+4lga的最大值为3，求a的值.

8.(2002年全国高考题)设f(x)=x²+x-a+1　x∈R.

(1)判别函数f(x)的奇偶性；

(2)求f(x)的最小值.

基础训练10  等差数列与等比数列

●训练指要

理解数列的概念，能用函数的观点认识数列；了解数列的通项公式和递推公式的意义，会根据数列通项公式写出数列的任意一项，会根据数列递推公式写出数列的前几项.

一、选择题

1.数列1，3，6，10，…的一个通项公式是

A.a_n=n²-(n-1)　　　　　　　　　　　　　　　　　　　　　 B.a_n=n²-1

C.a_n=　　　　　　　　　　　　　　　　　　　　　D.a_n=

2.已知数列,3,,…,,那么9是数列的

A.第12项　　　　　　　　　　　　　　　　　　　　　　　　B.第13项

C.第14项　　　　　　　　　　　　　　　　　　　　　　　　D.第15项

3.数列{a_n}中，a₁=1,当n≥2时，n²=a₁a₂…a_n恒成立，则a₃+a₅等于

A.

二、填空题

4.数列{a_n}中，已知a_n=(-1)ⁿ·n+a(a为常数)且a₁+a₄=3a₂,则a=_________,a₁₀₀=_________.

5.数列11，103，1005，10007，…的一个通项公式是_________.

三、解答题

6.数列{a_n}的通项公式a_n=log_n+1(n+2)，求它的前30项之积.

7.数列{a_n}的通项a_n=c_n+,又知a₂=,a₄=,求a₁₀.

8.已知f(x)=2+数列a_n满足a_n=f(n)(n=1,2,3,…)

(1)1和32是否是{a_n}中的项？如果是，那么是第几项？

(2)由关系式b_n=2+构造一个新数列{b_n},问数列{b_n}中第几项最大？最大项是多少？

基础训练11　数列的通项与前n项和

●训练指要

掌握等差、等比数列前n项和的公式，了解推导公式的思想方法，会解已知a₁,d(q)n,a_n,S_n中某三个量，求另外量的基本问题.

一、选择题

1.数列通项为a_n=，当前n项和为9时，项数n是

A.9　　　　　　　　　　　 B.99　　　　　　　　　　　C.10　　　　　　　　　　　　　　D.100

2.(2003年安徽春季高考题)等差数列{a_n}中，若a₁₀=10,a₁₉=100,前n项和S_n=0,则n等于

A.7　　　　　　　　　　　 B.9　　　　　　　　　　　 C.17　　　　　　　　　　　　　　D.19

3.等差数列{a_n}中，a_n-4=30,且前9项的和S₉=18，前n项和为S_n=240,则n等于

A.15　　　　　　　　　　　　　　B.16　　　　　　　　　　　C.17　　　　　　　　　　　　　　D.18

二、填空题

4.在等比数列{a_n}中，a₇·a₁₁=6,a₄+a₁₄=5,则=_________.

5.已知等差数列{a_n}中，a₁、a₃、a₉成等比数列，则=_________.

三、解答题

6.已知等差数列{a_n} 中，a₅=a₁₄,a₂+a₉=31,求前10项的和.

7.(2000年全国高考题)设{a_n}为等差数列，S_n为数列{a_n}的前n项和，已知S₇=7，S₁₅=75，T_n为数列{}的前n项和，求T_n.

8.(2002年江苏高考题)设{a_n}为等差数列，{b_n}为等比数列，a₁=b₁=1,a₂+a₄=b₃,b₂b₄=a₃.

分别求出{a_n}及{b_n}的前10项和S₁₀及T₁₀.

基础训练12　数列的应用

●训练指要

等差、等比数列性质的综合运用；数列与函数、不等式、三角、几何等内容的综合运用.

一、选择题

1.(2002年上海春季高考题)设{a_n}是等差数列，S_n是前n项的和，且S₅<S₆,S₆=S₇>S₈，则下列结论错误的是

A.d<0　　　　　　　　　　　　　　　　　　　　　　　　　　 B.a₇=0　　　　　　　　　

C.S₉>S₅D.S₆、S₇均为S_n的最大值

2.在△ABC中，tanA是以-4为第三项，4为第七项的等差数列的公差，tanB是以为第三项，9为第六项的等比数列的公比，则这个三角形是

A.钝角三角形　　　　　　　　　　　　　　　　　　　　　　　　 B.锐角三角形

C.等腰三角形　　　　　　　　　　　　　　　　　　　　　　　　 D.非等腰的直角三角形

3.若关于x的方程x²-x+a=0和x²-x+b=0(a≠b)的四个根可组成首项为的等差数列，则a+b的值是

A.　　　　　　　　　　 B.　　　　　　　 C.　　　　　　　　　　　　　D.

二、填空题

4.{a_n}是等差数列，a₂=8,S₁₀=185,从{a_n}中依次取出第2项、第4项、第8项，…第2ⁿ项，按原来的顺序排成一个新数列{b_n}，则b_n=_________.

5.已知x、y为正实数，且x,a₁,a₂,y成等差数列，x,b₁,b₂,y成等比数列，则的取值范围是_________.

三、解答题

6.在5和81之间插入两个正数，使前三个数成等差数列，后三个数成等比数列，求这两个数的和.

7.(2002年上海高考题)已知函数f(x)=a·b^x的图象过A(4，)和B(5，1)

(1)求函数f(x)的解析式；

(2)记a_n=log₂f(n)，n是正整数，S_n是数列{a_n}的前n项和，解关于n的不等式a_nS_n≤0.

(3)对于(2)中的a_n与S_n，96是否为数列{a_nS_n}中的项？若是，则求出相应的项数；若不是，则说明理由.

8.已知函数y=log₂(n∈N^*).

(1)当n=1,2,3,…时，已知函数的图象和直线y=1的交点的横坐标依次记为a₁,a₂,a₃,….

求证：a₁+a₂+a₃+…+a_n<1.

(2)对每一个n∈N^*,设A_n、B_n为已知函数图象上与x轴距离为1的两点，求证：n取任意一个正整数时，以线段A_nB_n为直径的圆都与一条定直线相切，并求这条直线的方程和切点的坐标.

基础训练1答案

一、1.D　2.B  3.D　 二、4.{1,5,7,11,13,17,19}　5.1　 三、6.－

提示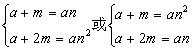：但要注意元素互异性，n≠1.

7.{x2≤x≤3或x=1},{2},{xx<1或x>3},{xx≤1或x>2},U, 　 8.{0,1,－}.

提示：不要忽视B=的情形.

基础训练4答案

一、1.D　2.C  3.A　 二、4. 4　5.(4,－2)　(2，－1)　 三、6. 1－x²(x≤0)

7.(1)f^－1(x)=1+ (x>2)　　(2)f^－1(x)=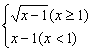　8.y=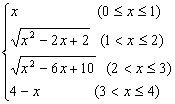

基础训练5答案

一、1.D　2.D  3.B 二、4.(－3,1)　5.三、6.x²－1(x≥1)　7.(1){x5≤x<10且x≠6}

(2)［－5,－π∪(－,)∪(π,5　(3)令u=2^x,t=log₂x那么中间变量u、t的值域都相同(都为原函数的定义域)，由u=2^x,x∈［－1,1］,∴≤2^x≤2,则≤log₂x≤2,∴≤x≤4,故f(log₂x)的定义域为［，4］.　8.f(x)=－

基础训练6答案

一、1.C　2.C  3.D　 二、4.(－∞,2)　(4,+∞)　5.②④　 三、6.(1)略　(2)－3<a<2

7.f(x)在(0，1］，［－1，0)上为减函数；在［1，+∞),(－∞,－1)上为增函数.　g(x)在(－∞,0),(0,+∞)上为增函数.　8.(1)证明略(－∞,0),(0,+∞)均为递增区间.　(2)0，0，f(x²)－5f(x)g(x)=0.

基础训练7答案

一、1.D　2.B  3.C　 二、4. 6　5.(－∞,］　三、6.(－1,0)　7.g(t)=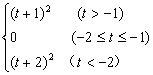

g(t)的最小值为0.　提示：讨论对称轴x=－1与区间端点t,t+1的关系.　8.［,18］

基础训练8答案一、1.C　2.D　3.B  二、4.

三、6.f(log₂3)=f(1+log₂3)=f(2+log₂3)=f(3+log₂3)=f(log₂24)=(.7.　8.(1)y=(a>1,t≠0)　(2)a=16,x=64

基础训练9答案一、1.D　2.C　3.D  二、4.2　5.　三、6. 1　7.　8.(1)既不是奇函数，也不是偶函数(2)a≤－时，f(x)最小值为－a;－<a≤时，f(x)的最小值是a²+1;当a>时，f(x)最小值是a+.

基础训练10答案

一、1.C　2.C  3.B二、4.－3　97  5.a_n=10ⁿ+2n－1三、6.5　7.

8.(1)1是第10或第20项，32不是(2)b_n=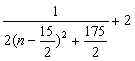∴第7项或第8项最大，最大值为

基础训练11答案

一、1.B　2.C  3.A二、4.三、6.1557.T_n=8.S₁₀=－

基础训练12答案

一、1.C　2.B  3.D二、4.3×2ⁿ+2　5.［4,+∞)三、6.707.(1)f(x)－·4^x (2)a_n=2n－10,S_n=2n(n－5)(n－9)　a_nS_n≤0，得n=5,6,7,8,9　(3)不是{a_nS_n}中的项　8.(1)知a_n=()ⁿ,  ∴a₁+a₂+…+a_n=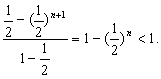　(2)知A_n,B_n两点坐标分别为(,1)和(2ⁿ,－1)，以A_nB_n为直径的圆的圆心C_n坐标是().　半径r=，即r=yC_n ∴所在圆C_n与y轴相切于原点.