普通高等学校招生全国统一考试数学分类汇编
第一章《集合与简易逻辑》
一、选择题（共27题）
1．（安徽卷）设集合
，
，则
等于（ ）
A．
B．
C．
D．
解：
，
，所以
，故选B。
2．（安徽卷）设
，已知命题
；命题
，则
是
成立的（ ）
A．必要不充分条件 B．充分不必要条件
C．充分必要条件 D．既不充分也不必要条件
解：命题是命题等号成立的条件，故选B。
3．（安徽卷）设全集
，集合
，
，则
等于（ ）
A． B．
C．
D．
解：
，则＝，故选B
4．（安徽卷）“
”是
“的（ ）
A．必要不充分条件 B．充分不必要条件
C．充分必要条件 D．既不充分也不必要条件
解：条件集是结论集的子集，所以选B。
5．（北京卷）设集合A=
，B=
，则A
B等于（ ）
(A) 
(B)
(C)｛xx>－3｝ (D)
｛xx<1｝
解：集合A=＝｛xx<1｝，借助数轴易得选A
6．（福建卷）已知全集U=R,且A=｛x︱︱x－1︱>2｝,B=｛x︱x
－6x+8<0｝，则(
A)∩B等于（ ）
A.[－1,4] B. (2,3) C. (2,3) D.(－1,4)
解：全集
且
∴(A)∩B =
，选C.
7．（福建卷）
是
的
（A）充分而不必要条件 （B）必要不而充分条件
（C）充要条件 （D）既不充分也不必要条件
解：若，则
，α不一定等于
；而若则tanα=1，∴ 是的必要不而充分条件，选B.
8．（湖北卷）有限集合
中元素的个数记做
，设
都为有限集合，给出下列命题：
①
的充要条件是
；
②
的充要条件是
；
③
的充要条件是；
④
的充要条件是
；
其中真命题的序号是
A．③④ B．①② C．①④ D．②③
解：①Û集合A与集合B没有公共元素，正确
②Û集合A中的元素都是集合B中的元素，正确
③Û集合A中至少有一个元素不是集合B中的元素，因此A中元素的个数有可能多于B中元素的个数，错误
④Û集合A中的元素与集合B中的元素完全相同，两个集合的元素个数相同，并不意味着它们的元素相同，错误,故选B
9．（湖北卷）集合P＝｛x」x2－16<0｝,Q＝｛x」x＝2n，n
Z｝,则P
Q＝
A.｛-2,2｝ B.｛－2，2，－4，4｝ C.｛2，0，2｝ D.｛－2，2，0，－4，4｝
解：P＝｛xx2－16<0｝＝｛x－4<x<4｝，故PQ＝｛－2，0，2｝，故选C
10．（湖南卷）“a=1”是“函数
在区间[1, +∞)上为增函数”的(
)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解：若“
”，则函数
=
在区间
上为增函数；而若在区间上为增函数，则0≤a≤1，所以“”是“函数在区间上为增函数”的充分不必要条件，选A.
11．（湖南卷）设函数
,集合M=
,P=
,若M
P,
则实数a的取值范围是 ( )
A.(-∞,1) B.(0,1) C.(1,+∞) D. [1,+∞)
解：设函数
, 集合
，若a>1时，M={x 1<x<a}；若a<1时M={x a<x<1}，a=1时，M=；
，∴
=
>0，∴ a>1时，P=R，a<1时，P=； 已知
,所以选C.
12．（江苏卷）若A、B、C为三个集合，
，则一定有
（A）
（B）
（C）
（D）
【思路点拨】本题主要考查.集合的并集与交集运算，集合之间关系的理解。
【正确解答】因为
由题意得
所以选A
【解后反思】对集合的子、交、并、补运算，以及集合之间的关系要牢固掌握。本题考查三个抽象集合之间的关系，可以考虑借助与文氏图。
13．（江西卷）已知集合M＝｛x
｝，N＝｛yy＝3x2＋1，xÎR｝，则MÇN＝（
）
A．Æ B. {xx³1} C.｛xx>1｝ D. {x x³1或x<0}
解：M＝｛xx>1或x£0｝，N＝｛yy³1｝故选C
14．（江西卷）已知集合
，
，则
等于（ ）
Ａ． Ｂ．
Ｃ．
Ｄ．
解：P＝｛xx³1或x£0｝，Q＝｛xx>1｝故选C
15．（江西卷）下列四个条件中，是的必要不充分条件的是（ ）
Ａ．
，
Ｂ．，
Ｃ．
为双曲线，
Ｄ．
，
解：A. p不是q的充分条件，也不是必要条件；B. p是q的充要条件；C. p是q的充分条件，不是必要条件；D.正确
16．（辽宁卷）设集合
,则满足
的集合B的个数是
(A)1 (B)3 (C)4 (D)8
【解析】，，则集合B中必含有元素3，即此题可转化为求集合的子集个数问题，所以满足题目条件的集合B共有
个。故选择答案C。
【点评】本题考查了并集运算以及集合的子集个数问题，同时考查了等价转化思想。
17．（全国卷I）设集合
，
，则
A．
B．
C．
D．
解：=
，=
，
∴ ，选B.
18．（全国II）已知集合M＝｛xx＜3｝，N＝｛xlog2x＞1｝，则M∩N＝
（A） （B）｛x0＜x＜3｝ （C）｛x1＜x＜3｝ （D）｛x2＜x＜3｝
解析:
,用数轴表示可得答案D
【点评】考察知识点有对数函数的单调性,集合的交集
19．（山东卷）设p：x－x－20>0,q：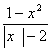
<0,则p是q的
（A）充分不必要条件 （B）必要不充分条件
（C）充要条件 （D）既不充分也不必要条件
解：p：x－x－20>0Ûx>5或x<－4，q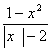：<0Ûx<－2或－1<x<1或x>2，借助图形知选A
20．（山东卷）设p∶
∶
0，则p是q的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
解：p：
Û－1<x<2，q：
0Ûx<－2或－1<x<2，故选A
21．(陕西卷)已知集合P={x∈N1≤x≤10},集合Q={x∈Rx2+x－6≤0}, 则P∩Q等于( )
A. {2} B.{1,2} C.{2,3} D.{1,2,3}
解：已知集合P={x∈N1≤x≤10}={1，2，3，……，10}，集合Q={x∈R x2+x－6=0} =
， 所以P∩Q等于{2} ，选A．
22．（四川卷）已知集合
，集合
，则集合
（A）
（B）
（C）
（D）
解：已知集合=
，集合
=
，则集合，选C.
23．（天津卷）设集合
，
，那么“
”是“
”的（ ）
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
解析：设集合，，
，所以若“”推不出“”；若“”，则“”，所以“”是“”的必要而不充分条件，选B.
24．（天津卷）已知集合
，
，则（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
解：已知集合
=
，则
＝
，选A.
25．（浙江卷）设集合
≤x≤2},B={x0≤x≤4},则A∩B=
(A)［0,2］ (B)［1,2］ (C)［0,4］ (D)［1,4］
【考点分析】本题考查集合的运算，基础题。
解析：
，故选择A。
26．(重庆卷)已知集合U={1,2,3,4,5,6,7}, A={2,4,5,7},B={3,4,5},则(uA)∪(uB)=
(A){1,6} (B){4,5} (C){1,2,3,4,5,7} (D){1,2,3,6,7}
解析：已知集合
，(
uA) ={1，3，6}，(uB) ={1，2，6，7}，则(uA)∪(uB)＝{1，2，3，6，7}，选D.
27．（上海春）若集合
，则A∩B等于( )
（A）
. （B）
. （C）
.
（D）
.
讲解：应用直接计算．由于函数y = 
, -1≤x≤1是增函数，则其值域为A=[-1,1]；由于函数y =2 — 
,
0≤x≤1是增函数，则其值域为B=（-∞,1]，所以A∩B=[-1，1]．故应该选B．
二、填空题（共3题）
28．（山东卷）下列四个命题中，真命题的序号有 （写出所有真命题的序号）.
①将函数y=
的图象按向量v=(－1,0)平移，得到的图象对应的函数表达式为y=
②圆x2+y2+4x+2y+1=0与直线y=
相交，所得弦长为2
③若sin(
+
)=
,sin(－)=
,则tancot=5
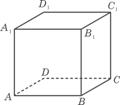
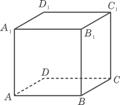
④如图，已知正方体ABCD- A1B1C1D1，P为底面ABCD内一动点，
P到平面AA1D1D的距离与到直线CC1的距离相等，则P点的轨迹是抛物线的一部分.
解：①错误，得到的图象对应的函数表达式应为y＝x－2
②错误，圆心坐标为（－2，1），到直线y=的距离为
>半径2，故圆与直线相离，
③正确，sin(+)=＝sincos＋cossin，sin(－)＝sincos－cossin＝，两式相加，得2 sincos＝
，两式相减，得2 cossin＝
，故将上两式相除，即得tancot=5
④正确，点P到平面AD1的距离就是点P到直线AD的距离，
点P到直线CC1就是点P到点C的距离，由抛物线的定义
可知点P的轨迹是抛物线。
二、填空题（共2题）
29．(上海卷)已知集合A＝
－1，3，2
－1
，集合B＝3，
．若B
A，则实数＝ ．
解：由
，经检验，
为所求；
30．(上海卷)已知
，集合
，若
,则实数
。
解：已知，集合，若, 则实数
。
三、解答题（共1题）
31．（全国II卷）设
，函数
若
的解集为A，
，求实数
的取值范围。
解：由f（x）为二次函数知
，令f（x）＝0解得其两根为
由此可知
（i）当
时，
的充要条件是
，即
解得
（ii）当
时，
的充要条件是
，即
解得
综上，使
成立的a的取值范围为