解析几何中的基本公式
1、
两点间距离：若
，则
特别地：
轴， 则
。
轴， 则
。
2、
平行线间距离：若
则：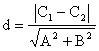
注意点：x，y对应项系数应相等。
3、
点到直线的距离：
则P到l的距离为：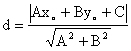
4、
直线与圆锥曲线相交的弦长公式：
消y：
，务必注意
若l与曲线交于A
则：
5、
若A，P（x，y）。P在直线AB上，且P分有向线段AB所成的比为
，
则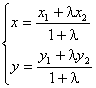
，特别地：=1时，P为AB中点且
变形后：
6、
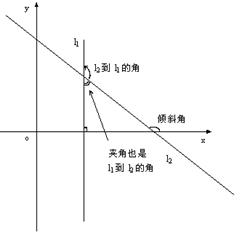
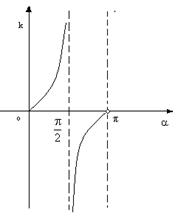
若直线l1的斜率为k1，直线l2的斜率为k2，则l1到l2的角为
适用范围：k1，k2都存在且k1k2
－1 ， 
若l1与l2的夹角为
，则
，
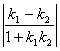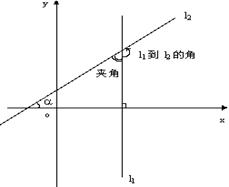
注意：（1）l1到l2的角，指从l1按逆时针方向旋转到l2所成的角，范围
l1到l2的夹角：指 l1、l2相交所成的锐角或直角。
（2）l1
l2时，夹角、到角=
。
（3）当l1与l2中有一条不存在斜率时，画图，求到角或夹角。
7、
（1）倾斜角
，
；
（2）
；
（3）直线l与平面
；
（4）l1与l2的夹角为，
，其中l1//l2时夹角=0；
（5）二面角
；
（6）l1到l2的角
8、
直线的倾斜角与斜率k的关系
a)
每一条直线都有倾斜角，但不一定有斜率。
b)
若直线存在斜率k，而倾斜角为，则k=tan。
9、 直线l1与直线l2的的平行与垂直
（1）若l1，l2均存在斜率且不重合：①l1//l2
k1=k2
②l1l2 k1k2=－1
（2）若
若A1、A2、B1、B2都不为零
① l1//l2
；
② l1l2 A1A2+B1B2=0；
③ l1与l2相交
④ l1与l2重合
；
注意：若A2或B2中含有字母，应注意讨论字母=0与0的情况。
10、 直线方程的五种形式
名称 方程 注意点
斜截式： y=kx+b 应分①斜率不存在
②斜率存在
点斜式：
（1）斜率不存在：
（2）斜率存在时为
两点式：
截距式：
其中l交x轴于
，交y轴于
当直线l在坐标轴上，截距相等时应分：
（1）截距=0 设y=kx
（2）截距=
设
即x+y=
一般式：
（其中A、B不同时为零）
10、确定圆需三个独立的条件
圆的方程 （1）标准方程：
， 
。
（2）一般方程：
，（
11、直线与圆的位置关系有三种
若
，
12、两圆位置关系的判定方法
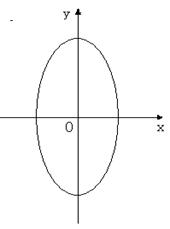设两圆圆心分别为O1，O2，半径分别为r1，r2，
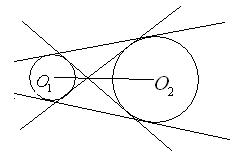
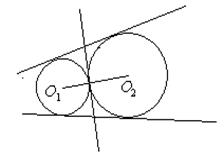
外离 外切
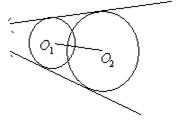
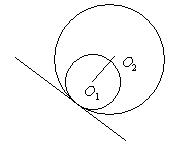
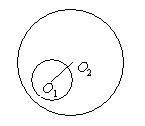
相交 内切 内含
13、圆锥曲线定义、标准方程及性质
（一）椭圆
定义Ⅰ：若F1，F2是两定点，P为动点，且
（为常数）则P点的轨迹是椭圆。
定义Ⅱ：若F1为定点，l为定直线，动点P到F1的距离与到定直线l的距离之比为常数e（0<e<1），则P点的轨迹是椭圆。
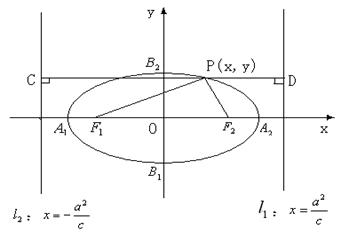标准方程：
定义域：
值域：
长轴长=
，短轴长=2b
焦距：2c
准线方程：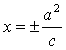
焦半径：
，
，
，
等（注意涉及焦半径①用点P坐标表示，②第一定义。）
注意：（1）图中线段的几何特征：
，
，
等等。顶点与准线距离、焦点与准线距离分别与
有关。
（2）
中经常利用余弦定理、三角形面积公式将有关线段
、
、2c，有关角
结合起来，建立+、
等关系
（3）椭圆上的点有时常用到三角换元：
；
（4）注意题目中椭圆的焦点在x轴上还是在y轴上，请补充当焦点在y轴上时，其相应的性质。
二、双曲线
（一）定义：Ⅰ若F1，F2是两定点，
（为常数），则动点P的轨迹是双曲线。
Ⅱ若动点P到定点F与定直线l的距离之比是常数e（e>1），则动点P的轨迹是双曲线。
（二）图形：
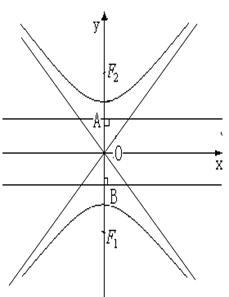
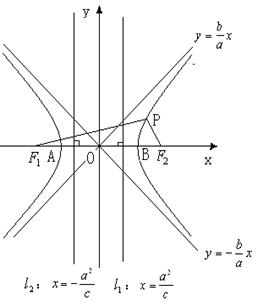
（三）性质
方程：
定义域：
； 值域为R；
实轴长=，虚轴长=2b
焦距：2c
准线方程：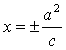
焦半径：，，
；
注意：（1）图中线段的几何特征：
，
顶点到准线的距离：
；焦点到准线的距离：
两准线间的距离=
（2）若双曲线方程为
渐近线方程：
若渐近线方程为
双曲线可设为
若双曲线与有公共渐近线，可设为
（
，焦点在x轴上，
，焦点在y轴上）
（3）特别地当
离心率
两渐近线互相垂直，分别为y=
，此时双曲线为等轴双曲线，可设为
；
（4）注意中结合定义
与余弦定理
，将有关线段、、
和角结合起来。
（5）完成当焦点在y轴上时，标准方程及相应性质。
二、抛物线
（一）定义：到定点F与定直线l的距离相等的点的轨迹是抛物线。
即：到定点F的距离与到定直线l的距离之比是常数e（e=1）。
（二）图形：
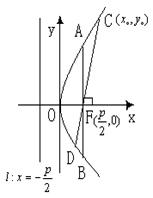
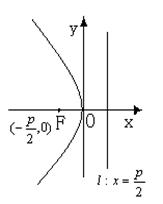
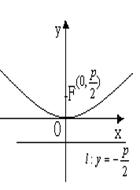
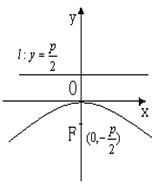
（三）性质：方程：
；
焦点： 
，通径
；
准线： 
；
焦半径：
过焦点弦长
注意：（1）几何特征：焦点到顶点的距离=
；焦点到准线的距离=
；通径长=
顶点是焦点向准线所作垂线段中点。
（2）抛物线
上的动点可设为P
或
P