普通高等学校春季招生考试高三数学
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页．第Ⅱ卷3至9页，共150分，考试时间120分钟．
第Ⅰ卷（选择题 共60分）
注意事项
1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上．
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．
3．考试结束，监考人将本试卷和答题卡一并收回．
|
三角函数的积化和差公式
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．
（1）若集合M＝{y y=2－x}，
，则
（2）若
，则方程f(4x)=x的根是
（A）
（B）
（C）
（D）－2
（3）设复数z1=－1＋i，
，则
（A）
（B）
（C）
（D）
（4）函数
的最大值是
（A）
（B）
（C）
（D）
（5）在同一坐标系中，方程a2x2+b2y2=1与ax+by2=0（a>b>0）的曲线大致是
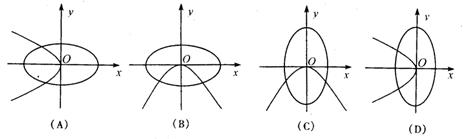
（6）若A，B，C是△ABC的三个内角，且A<B<C（
），则下列结论中正确的是
（A）sinA<sinC （B）cosA<cosC
（C）tanA<tanC （D）cotA<cotC
（7）椭圆
（j为参数）的焦点坐标为
（A）（0，0），（0，－8） （B）（0，0），（－8，0）
（C）（0，0），（0，8）
（D）(0，0)，（8，0）
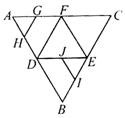
（8）如图，在正三角形ABC中，D，E，F分别为各边的中点， G，
H，I，J分别为AF，AD，BE，DE的中点．将△ABC沿DE，EF，
DF折成三棱锥以后，GH与IJ所成角的度数为
（A）90° （B）60° （C）45° （D）0°
（9）某班新年联欢会原定的5个节目已排成节目单，开演前又增加了两个新节目．如果将这两个节目插入原节目单中，那么不同插法的种数为
（A）42 （B）30 （C）20 （D）12
（10）已知直线ax+by+c=0（abc≠0）与圆x2+y2=1相切，则三条边长分别为 a ， b ， c 的三角形
（A）是锐角三角形 （B）是直角三角形
（C）是钝角三角形 （D）不存在
（11）若不等式 ax+2 < 6的解集为（－1，2），则实数a等于
（A）8 （B）2 （C）－4 （D）－8
（12）在直角坐标系xOy中，已知△AOB三边所在直线的方程分别为x＝0，y＝0，2x+3y=30，则△AOB内部和边上整点（即横、纵坐标均为整数的点）的总数是
（A）95 （B）91
（C）88 （D）75
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上．
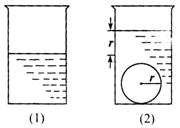（13）如图，一个底面半径为R的圆柱形量杯中装有适量的
水．若放入一个半径为r的实心铁球，水面高度恰好升
高r，则
____________．
（14）在某报《自测健康状况》的报道中，自测血压结果与相
应年龄的统计数据如下表，观察表中数据的特点，用适当的数填入表中空白（____）内．
| 年龄（岁） | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 |
| 收缩压（水银柱 毫米） | 110 | 115 | 120 | 125 | 130 | 135 | （___） | 145 |
| 舒张压（水银柱 毫米） | 70 | 73 | 75 | 78 | 80 | 83 | （___） | 88 |
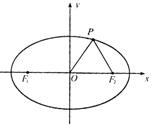（15）如图，F1，F2分别为椭圆
的左、右焦点，点P
在椭圆上△POF2是面积为
的正三角形，则b2的值是
_________________．
（16）若存在常数p>0，使得函数f(x)满足
（x∈R），则f(x)的一个正周期为_____________．
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤．
（17）（本小题满分12分）
解不等式：
．
（18）（本小题满分12分）
已知函数
，求f(x)的定义域，判断它的奇偶性，并求其值域．
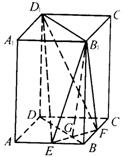（19）（本小题满分12分）
如图，正四棱柱ABCD－A1B1C1D1中，底面边长为
，侧棱长为4．E，F分别为棱AB，BC的中点，
．
（Ⅰ）求证：平面B1EF⊥平面BDD1B1；
（Ⅱ）求点D1到平面B1EF的距离d；
（Ⅲ）求三棱锥B1－EFD1的体积V．
（20）（本小题满分12分）
某租赁公司拥有汽车100辆．当每辆车的月租金为3000元时，可全部租出．当每辆车的月租金每增加50元时，未租出的车将会增加一辆．租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护需50元．
（Ⅰ）当每辆车的月租金定为3600元时，能租出多少辆车？
（Ⅱ）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？
（21）（本小题满分13分）
如图，在边长为l的等边△ABC中，圆O1为△ABC的内切圆，圆O2与圆O1外切，且与AB，BC相切，…，圆On+1与圆On外切，且与AB，BC相切，如此无限继续下去．记圆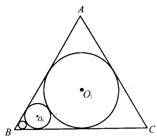
On的面积为an（n∈N）．
（Ⅰ）证明｛an｝是等比数列；
（Ⅱ）求
的值．
（22）（本小题满分13分）
已知动圆过定点P（1，0），且与定直线l：x＝－1相切，点C在l上．
（Ⅰ）求动圆圆心的轨迹M的方程；
（Ⅱ）设过点P，且斜率为
的直线与曲线M相交于A，B两点．
（ⅰ）问：△ABC能否为正三角形？若能，求点C的坐标；若不能，说明理由；
（ⅱ）当△ABC为钝角三角形时，求这种点C的纵坐标的取值范围．
普通高等学校春季招生考试
参考解答
一、选择题：本题主要考查基本知识和基本运算，每小题5分，满分60分．
（1）C （2）A （3）C （4）D （5）D （6）A
（7）D （8）B （9）A （10）B （11）C （12）B
二、填空题：本题主要考查基本知识和基本运算．每小题4分，满分16分．
（13）
（14）
| 年龄（岁） | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 |
| 收缩压（水银柱 毫米） | 110 | 115 | 120 | 125 | 130 | 135 | （140） | 145 |
| 舒张压（水银柱 毫米） | 70 | 73 | 75 | 78 | 80 | 83 | （85） | 88 |
（15）
（16）
注：填的正整数倍中的任何一个都正确．
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
（17）本小题主要考查不等式的解法、对数函数的性质等基本知识，考查运算能力和逻辑思维能力．满分12分．
解：原不等式变形为
．
所以，原不等式
．
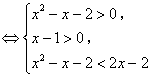
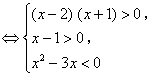
故原不等式的解集为｛x 2<x<3｝．
（18）本小题主要考查三角函数的基本知识，考查逻辑思维能力、分析和解决问题的能力．满分12分．
解：由cos2x≠0得
，解得 
，k∈Z．
所以f(x)的定义域为
．
因为f(x)的定义域关于原点对称，且
，
所以f(x)是偶函数．
当，k∈Z时，
＝3cos2x－1
所以f(x)的值域为
．
（19）本小题主要考查正四棱柱的基本知识，考查空间想象力、逻辑思维能力和运算能力．满分12分．
（Ⅰ）证法一：
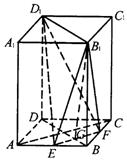连结AC．
∵ 正四棱柱ABCD－A1B1C1D1的底面是正方形，
∴ AC⊥BD，又AC⊥D1D，
故 AC⊥平面BDD1B1．
∵ E，F分别为AB，BC的中点，故 EF∥AC，
∴ EF⊥平面BDD1B1，
∴ 平面B1EF⊥平面BDD1B1．
证法二：
∵ BE＝BF，∠EBD＝∠FBD＝45°，
∴ EF⊥BD．
又 EF⊥D1D，
∴ EF⊥平面BDD1B1，
∴ 平面B1EF⊥平面BDD1B1．
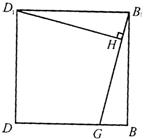（Ⅱ）在对角面BDD1B1中，作D1H⊥B1G，垂足为H．
∵ 平面B1EF⊥平面BDD1B1，且平面B1EF
平面BDD1B1＝B1G，
∴ D1H⊥平面B1EF，且垂足为H，
∴ 点D1到平面B1EF的距离d= D1H．
解法一：
在Rt△D1HB1中，D1H＝D1B1·sin∠D1B1H．
∵ 
，
，
∴ 
．
解法二：
∵ △D1HB1∽△B1BG，
∴ 
，
∴ 
．
解法三：
连结D1G，则三角形D1GB1的面积等于正方形DBB1D1面积的一半，
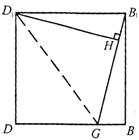即 
，
∴ 
．
（Ⅲ）
．
（20）本小题主要考查二次函数的性质等基本知识，考查分析和解决问题的能力．满分12分．
解：（Ⅰ）当每辆车的月租金定为3600元时，未租出的车辆数为
，所以这时租出了88辆车．
（Ⅱ）设每辆车的月租金定为x元，则租赁公司的收益为
，
整理得
．
所以，当x=4050时，f(x)最大，最大值为f(4050)＝307050，
即当每辆车的月租金定为4050时，租赁公司的月收益最大，
最大月收益为307050元．
（21）本小题主要考查数列、数列极限、三角函数等基本知识，考查逻辑思维能力．满分13分．
（Ⅰ）证明：记rn为圆On的半径，则
，
．
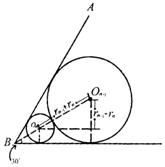
所以
（n≥2），
于是 
，
，
故｛an｝成等比数列．
（Ⅱ）解：因为
（n∈N），
所以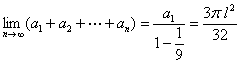
．
（22）本小题主要考查直线、圆与抛物线的基本概念及位置关系，考查运用解析几何的方法解决数学问题的能力．满分13分．
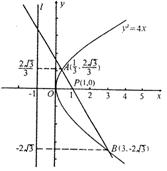解：（Ⅰ）依题意，曲线M是以点P为焦点，直线l为准线的抛物线，所以曲线M的方程为y2=4x．
（Ⅱ）（ⅰ）由题意得，直线AB的方程为
．
由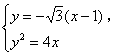
消y得3x2－10x+3＝0，
解得 
，x2＝3．
所以A点坐标为
，B点坐标为
，
．
假设存在点C（－1，y），使△ABC为正三角形，则 BC ＝ AB 且 AC ＝ AB ，即
|
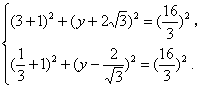
由①－②得
，
解得 
．
但 不符合①，
所以 由①，②组成的方程组无解．
因此，直线l上不存在点C，使得△ABC是正三角形．
（ⅱ）解法一：
设C（－1，y）使△ABC成钝角三角形，由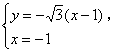
得
，
即当点C的坐标为
时，A，B，C三点共线，故
．
又 
，
．
当 BC 2 > AC 2 + AB 2，即
，即
时，∠CAB为钝角．
当 AC 2 > BC 2 + AB 2，即
，即
时，∠CBA为钝角．
又 AB 2 > AC 2 + BC 2，即
，即
，
．
该不等式无解，所以∠ACB不可能为钝角．
因此，当△ABC为钝角三角形时，点C的纵坐标y的取值范围是
或
（）．
解法二：
以AB为直径的圆的方程为
．
圆心
到直线l：x=－1的距离为
，
所以，以AB为直径的圆与直线l相切于点
．
当直线l上的C点与G重合时，∠ACB为直角，当C与G点不重合，且
A，B，C三点不共线时，∠ACB为锐角，即△ABC中∠ACB不可能是钝角。
因此，要使△ABC为钝角三角形，只可能是∠CAB或∠CBA为钝角。
过点A且与AB垂直线的直线方程为
．
令 x=－1得 
．
过点B且与AB垂直线的直线方程为
．
令 x=－1得 
．
又由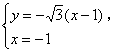解得，
所以，当点C的坐标为时，A，B，C三点共线，不构成三角形。
因此，当△ABC为钝角三角形时，点C的纵坐标y的取值范围是
或（）．