高三数学周练试卷
一、选择题:本大题共12小题,每小题5分,共60分。
1.![]() 的( )
的( )
A.必要非充分条件 B.充分非必要条件
C.充分必要条件 D.既非充分又非必要条件
2.等差数列![]() 中,
中,![]() ,则此数列的前13项和为( )
,则此数列的前13项和为( )
A.13 B.52 C. 26 D.156
3.若![]() 的值域为
的值域为![]() ,则
,则![]() 的值域为
( )
的值域为
( )
A.![]() B.
B.![]() C.
C.![]() D.以上都不对
D.以上都不对
4.如果![]() 且
且![]() ,那么以下不等式正确的个数是
(
)
,那么以下不等式正确的个数是
(
)
①![]() ②
②![]() ③
③![]() ④
④![]() ⑤
⑤![]()
A.2 B.3 C.4 D.5
5.函数![]() 的图象大致为 ( )
的图象大致为 ( )
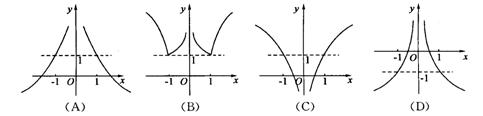
6.等比数列![]() 的首项
的首项![]() ,前
,前![]() 项和为
项和为![]() ,已知
,已知![]() ,则
,则![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.2
D.
C.2
D.![]()
7.集合M={x![]() <x≤6},不等式
<x≤6},不等式![]() >1解集是P,若P
>1解集是P,若P![]() M,则实数m的取值范围( ) A. [-
M,则实数m的取值范围( ) A. [-![]() , 5] B. [-3, -
, 5] B. [-3, -![]() ] C. [-3, 5] D. [-3, -
] C. [-3, 5] D. [-3, -![]() ]∪(-
]∪(-![]() , 5)
, 5)
8.已知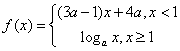 是
是![]() 上的减函数,那么
上的减函数,那么![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.把函数![]() 的图象沿向量
的图象沿向量![]() 的方向平移后,所得的图象关于y轴对称,则m的最小值是( )
的方向平移后,所得的图象关于y轴对称,则m的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知![]() ,点C在∠AOB内,且∠AOC=45°,设
,点C在∠AOB内,且∠AOC=45°,设![]() ,则
,则![]() 等于 (
)
等于 (
)
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
11.已知![]() 设数列
设数列![]() 满足
满足![]() ,则数列
,则数列![]() 的前
的前![]() 项和
项和![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.平面直角坐标系中,![]() 为坐标原点,已知两点
为坐标原点,已知两点![]() (2,-1),
(2,-1),![]() (-1,3),若点
(-1,3),若点![]() 满足
满足![]() 其中0≤
其中0≤![]() ≤1,且
≤1,且![]() ,则点
,则点![]() 轨迹方程为( )
轨迹方程为( )
A.![]() (-1≤
(-1≤![]() ≤2) B.
≤2) B. ![]() (-1≤
(-1≤![]() ≤2)
≤2)
C. ![]() D.
D.
![]()
二、填空题:本大题共6小题,每小题5分,共30分,把答案填在横线上.
13.已知![]() 是定义在
是定义在![]() 上的偶函数,且在
上的偶函数,且在![]() 上单调递增,
上单调递增,![]() ,则
,则![]() 的取值范围是: ;
的取值范围是: ;
14.设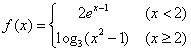 ,则不等式
,则不等式![]() >2的解集为 :_________________;
>2的解集为 :_________________;
15.在数列![]() 中,
中,![]() ,则此数列的前2006项之和为:____________;
,则此数列的前2006项之和为:____________;
16.若![]() 则
则![]() ;
;
17.函数 ![]() 在[-4,-2]上是增函数, 则a取值范围:______;
在[-4,-2]上是增函数, 则a取值范围:______;
18.给出以下结论:
① 通项公式为an=a1(![]() )n-1的数列一定是以a1为首项,
)n-1的数列一定是以a1为首项,![]() 为公比的等比数列;
为公比的等比数列;
② 函数![]() 是最小正周期为
是最小正周期为 ![]() ; ③函数y=
; ③函数y=![]() 在定义域上是单调递减的;
在定义域上是单调递减的;
④ ![]() ; ⑤函数y =log
; ⑤函数y =log![]() (4-x2)的值域是[-2,+∞).
(4-x2)的值域是[-2,+∞).
其中正确的是:______________.
三、解答题:本大题共![]() 小题,共60分.解答应写出文字说明,证明过程或演算步骤.
小题,共60分.解答应写出文字说明,证明过程或演算步骤.
19.(本小题满分12分)
已知: 命题![]() 是
是![]() 的反函数,且
的反函数,且![]() .
.
命题![]() 集合
集合![]() ,
,![]() ,且
,且![]() .求实数
.求实数![]() 的取值范围,使命题
的取值范围,使命题![]() 、
、![]() 有且只有一个是真命题.
有且只有一个是真命题.
20.(本题满分12分)
已知x∈R,=(2acos2x,1),=(2,2asin2x+2-a),y=·,
⑴求y关于x的函数解析式y=f (x),并求其最小正周期(a≠0时);
⑵当x∈[0,]时,f (x)的最大值为5.求a的值及函数y=f (x)(x∈R)的单调递增区间.
21.(本题满分12分)
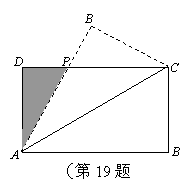
如图,设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后,交DC于点P. 设AB=x,
求△![]() 的最大面积及相应的x值.
的最大面积及相应的x值.
22.(本小题满分12分)
已知二次函数![]() 同时满足:①不等式
同时满足:①不等式![]() 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在![]() ,使得不等式
,使得不等式![]() 成立。设数列
成立。设数列![]() 的前
的前![]() 项和
项和![]() ,
,
(1)求函数![]() 的表达式;(2)求数列
的表达式;(2)求数列![]() 的通项公式;
的通项公式;
(3)设各项均不为零的数列![]() 中,所有满足
中,所有满足![]() 的正整数
的正整数![]() 的个数称为这个数列
的个数称为这个数列![]() 的变号数。令
的变号数。令![]() (
(![]() 为正整数),求数列
为正整数),求数列![]() 的变号数。
的变号数。
23.(本题满分12分)
已知函数![]() 的图象关于点
的图象关于点![]() 对称.
对称.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)若数列![]() ,
,![]() 满足
满足![]()
![]()
![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(Ⅲ)记![]() 若
若![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.