高三数学专项训练——解答题
【经典回顾一2006】已知锐角△ABC中,角A、B、C的对边分别是a、b、c,tanB=
⑴求角B的大小；
⑵求sin(B+10
)[1-
]的值.
【经典回顾二2006】已知函数
在x=
时都取得极值.
⑴求a、b的值及函数
的单调区间；
⑵若对
，不等式
恒成立，求c的取值范围.
【经典回顾三2006山东】、如图:在直角梯形ABCP中，BC∥AP，AB⊥BC，CD⊥AP，AD=DC=PD=2，E、F、G分别是线段PC、PD、BC的中点，现将△PDC折起，使平面PDC⊥平面ABCD
⑴ 求证：AP∥平面EFG；
⑵求二面角G-EF-D的大小；
⑶在线段PB上确定一点Q，使PC⊥平面ADQ,给出证明.
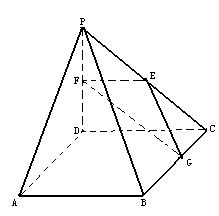
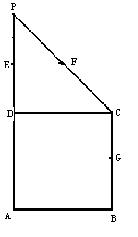
⑴ ⑵
【经典回顾四2006重庆】、如图：对每个正整数n，
是抛物线
上的点，过焦点F的直线
，交抛物线于另一点
.
⑴试证：
⑵取
并记
为抛物线上分别以
为切点的两条切线的交点.试证:
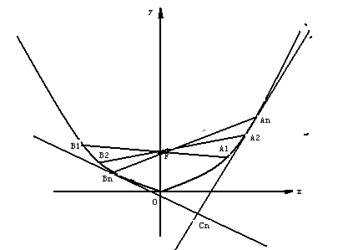
【经典回顾五2006】在直角坐标系中,已知向量
,
(
),
的最小值为1,
动点P同时满足下列三个条件:⑴
;⑵
⑶动点P的轨迹C经过点
B(0,-1) ㈠求曲线C的方程; ㈡是否存在方向向量m=(1,k)(k
)的直线L,L与曲线C相交于M、N两点，使
，且
与
的夹角为
？若存在，求出k，并求出直线L的方程；若不存在，请说明理由.