高三数学综合练习(一)

高三数学综合练习(一)

一、选择题：

 (1)设全集为U，集合M=，N=，则　　　　　　　　　　　 (　　)

　(A)M∩N∈M　　　　　　　　 (B)MNÍM

　(C)C_uAC_uB=　 　　　　　 (D)(_UN)∩MÍM

(2)在在⊿ABC中，sin2A=sin2B是A=B的　　　　　　　　　　　　　　　　 （　　）

　  (A)充分不必要条件　 　　 (B)必要不充分条件

(C)充分必要条件　　　　　(D)既不充分也不必要条件

(3) 已知a、b是两条不重合的直线，a、b是两个不重合的平面，给出四个命题：

1a//b，b//a；2a、bÌa，a//b，b//b，则a//b；

3a与a成30°的角，a⊥b，则b与a成60°的角；4a⊥a，b//a，则a⊥b。

其中正确命题的个数是：　　　　　　　　　　　　　　　　　　　　　　  　 （　　）

A.4个　　　　　　　　　　 B.3个　　　　　　　 C.2个　　　　　　　 D.1个

 (4)已知等比数列{a_n}的前n项和为S_n,S₃=3,S₆=27,则此等比数列的公比q等于 　(　　)

（A）2　　　　  （B）-2　　　　  (C)　　　　(D)-

 (5)从4位男教师和3女教师中选出3位教师，派往郊区3所学校支教，每校1人。要求这3位教师中男、女教师都要有，则不同的选派方案共有　　　　　　　　　　  　(　　)

　  (A)210种　　　　(B)186种　　(C)180种　　(D)90种

(6)已知函数f（x）=-在区间M上的反函数是其本身，则M可以是  　 (　　)

A.[-2,2]　　　  B.[-2,0]　　 C.[0,2]　　　 D.[-2,0]

(7)已知：椭圆的焦点是F₁、F₂，P是椭圆上一个动点，过点F₂向∠F₁PF₂的外角平分线作垂线，垂足为M，则点M的轨迹是　　　　　　　　　　　　　　　　　　　　  （　　）

（A)圆　　　　　(B)椭圆　　　　 (C)直线　 　 (D)双曲线的一支

(8)已知计算机中的某些存储器有如下特性：若存储器中原有数据个数为m个，则从存储器取出n个数据后，此存储器中的数据个数为m-n个；若存储器中原有数据为 m个，则将n个数据存入存储器后，此存储器中数据个数为m+n个。

现已知计算机中A、B、C三个存储器中数据个数均为0，计算机有如下操作：

第一次运算：在每个存储器中存入个数相同且个数不小于2 的数据；

第二次运算：从A存储器取出2个数据，将这2 个数据存入B存储器中；

第三次运算：从C存储器中取出1个数据，将这一个数据存入B存储器中；

第四次运算：从B存储器中取出与A存储器中个数相同的数据，将取出的数据存入A存储器，则这时B存储器中数据个数是　　　　　　　　　　　　　　　　　　　　 （　　)

　  (A)　8　　　　　(B)　7　 　　　　 (C)6　　　　　　(D)　5

二、填空题：本大题共6小题，每小题5分，共30分．将答案填在题中横线上．

(9)设复数=l+2i，=2-i，则等于　　　　　　　　 ．

 (10)若的展开式中x⁴的系数是240 ，则实数a的值是　　　　  ．

(11)圆x²+y²+4x-2y+4=0上的点到直线x-y-1=0的最大距离与最小距离的差为　　　　 ．

(12)已知一个球与一个二面角的两个半平面都相切，若球心到二面角的棱的距离是，切点到二面角棱的距离是1，则球的表面积是　　　　,球的体积是　　　 。

(13) 已知向量a= （2，3），b=2,则a=　　　　,b的坐标是　　　 。

(14)已知函数f(x)=且不等式f(x)≥a的解集是（－∞，２）］∪［０，２］，则实数a 的值是　　　　　 。　

三、解答题：

(15)(本小题满分13分)

已知向量a=(cosx,sinx),b=(-cosx,cosx),函数f(x)=2a×b+1

(Ⅰ)求函数f(x)的最小正周期；

（Ⅱ）当x∈[0,2]时，求f(x)的单调减区间。

(16)(本小题满分13分)甲、乙两支篮球队进行比赛，已知每一场甲队获胜的概率为0.6，乙队获胜的概率为0.4,每场比赛均要分出胜负，比赛时采用三场两胜制，即先取得两场胜利的球队胜出。

（Ⅰ）求甲队以二比一获胜的概率；

（Ⅱ）求乙队获胜的概率；

（Ⅲ）若比赛采用五局三胜制，试问甲获胜的概率是增大还是减小，请说明理由。 （理科）

 (17)(本小题满分13分)

如图棱长为1的正四面体ABCD中，E、F分别是棱AD、CD的中点，O是点A在平面BCD内的射影。

（Ⅰ）求直线EF与直线BC所成角的大小；

（Ⅱ）求点O到平面ACD的距离；

（Ⅲ）求二面角A-BE-F的大小。

(18)(本小题满分13分)

已知函数f(x)=x³+ax²+bx+c在x=1处有极值，f(x)在x=2处的切线l不过第四象限且倾斜角为，坐标原点到切线l的距离为。

（Ⅰ）求a、b、c的值；

（Ⅱ）求函数y=f(x)在区间[-1，]上的最大值和最小值。

(19)(本小题满分14分)

已知双曲线的中心在原点O，右焦点为F(c,0)，Ｐ是双曲线右支上一点，且⊿OFP的面积为

(I)若点P的坐标为（２，），求此双曲线的离心率；

(Ⅱ)若＝（-1）c²,当取得最小值时 ，求此双曲线的方程。

(20)(本小题满分14分)

（理科）已知数列前n项和为，点（n,）在直线y=x+上。数列{b_n}满足

b_n+2-2b_n+1+b_n=0(n∈N),且b₃=11,前9项和为153。

(I)　　　　　  求数列 、{b_n}的通项公式；

(II)　　　  设c_n=,数列{c_n}的前n项和T_n.求使不等式T_n>对一切n∈N都成立的最大正整数k的值；

(III)　  设f(n)=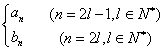,是否存在m∈N,使得f(m+15)=5f(m)成立？

若存在，求出m的值；若不存在，请说明理由。