高三数学第9讲
一、本讲复习内容
三角函数的概念、性质和图象
二、复习要求（以下内容摘自《考纲》）
1. 理解弧度的意义，并能正确进行弧度和角度的换算．
2. 掌握任意角的三角函数的定义、三角函数的符号、特殊角的三角函数值、三角函数的性质、同角三角函数的关系式与诱导公式，了解周期函数和最小正周期的意义．会求y＝Asin(ωx＋j)的周期，或者经过简单的恒等变形可化为上述函数的三角函数的周期，能运用上述三角公式化简三角函数式，求任意角的三角函数值与证明较简单的三角恒等式．
3. 了解正弦、余弦、正切、余切函数的图象的画法，会用“五点法”画正弦、余弦函数和函数y＝Asin(ωx＋j)的简图，并能解决与正弦曲线有关的实际问题．
4.正弦函数、余弦函数的对称轴，对称点的求法。
5．形如
的辅助角的形式，求最大、最小值的总题。
6．同一问题中出现
，求它们的范围。如求
的值域。
7．已知正切值，求正弦、余弦的齐次式的值。
如已知
的值。
8 正弦定理：
余弦定理：
，…
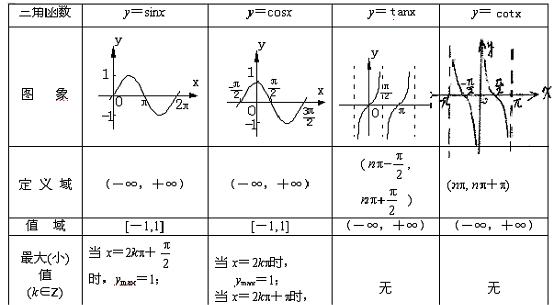
可归纳为表9－1.
表9-1 三角函数的图象三、主要内容及典型题例
三角函数是六个基本初等函数之一，三角函数的知识包括三角函数的定义、图象、性质、三角函数线、同角三角函数的关系式与诱导公式，以及两角和与差的三角函数，二倍角，降次公式等。
1. 三角函数的图象与性质和性质
2. 三角函数作为基本初等函数，它必然具备函数的共性；作为个体，它又具有自身的个性特点．例如周期性、弦函数的有界性，再如三角函数的单调性，具有分段单调的特征．通过复习对这些特性必须很好掌握，其中三角函数的周期性是高考中出现频率最高的试题．根据《考纲》的要求，只需要会求经过简单的恒等变形可化为正弦、余弦、正切、余切函数及y＝Asin(ωx＋j)等形式的三角函数的周期，不必去研究周期函数的和、差、积、商的函数的周期．
看一看历年来高考中出现的求三角函数周期的考题（例1），你应该对复习的要求有个基本的了解．
例１
求下列三角函数的周期．（根据历年全国高考有关考题(填空、选择题)改编
注意 理解函数周期这个概念，要注意不是所有的周期函数都有最小正周期，如常函数f(x)＝c（c为常数）是周期函数，其周期是异于零的实数，但没有最小正周期．
3. 弦函数的有界性：sinx≤1,cosx≤1在解题中有着广泛的应用，忽视这一性质，常会出现错误。
例3 求下列函数的值域：
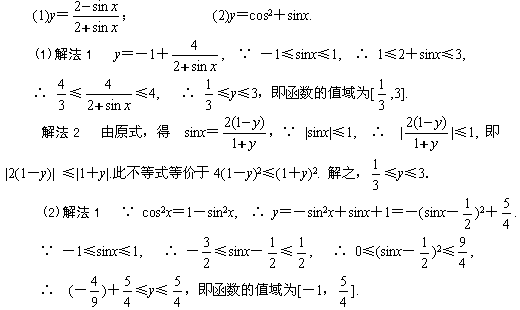
解法2 令t＝sinx，则f(t)＝－t2＋t＋1，∵ sinx≤1, ∴ t≤1.问题转化为求关于t的二次函数f(t)在闭区间[－1,1]上的最值．
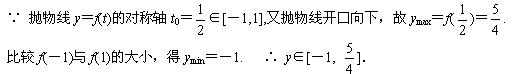
本例题(2)解法2通过换元，将求三角函数的最值问题转化为求二次函数在闭区间上的最值问题，从而达到解决问题的目的，这就是转换的思想．善于从不同角度去观察问题，沟通数学各学科之间的内在联系，是实现转换的关键，转换的目的是将数学问题由陌生化熟悉，由复杂化简单，一句话：由难化易．可见化归是转换的目的，而转换是实现化归段手段。
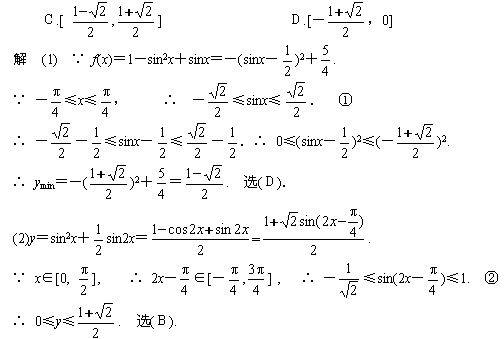
5. “去负——脱周——化锐”，是对三角函数式进行角变换的基本思路．即利用三角函数的奇偶性将负角的三角函数变为正角的三角函数——去负；利用三角函数的周期性将任意角的三角函数化为角度在区间[0o,360o)或[0o,180o)内的三角函数——脱周；利用诱导公式将上述三角函数化为锐角三角函数——化锐.
同角三角函数之间的三种关系：
(1)倒数关系：(2)商数关系： (3)平方关系：
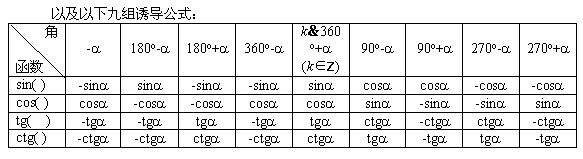
是进行三角式化简的最基本的公式，必须熟练掌握．
其中九组三角诱导公式的规律可简记为：奇变偶不变，符号看象限．此外在应用时，不论a取什么值，我们始终视a为锐角．否则，将导致错误。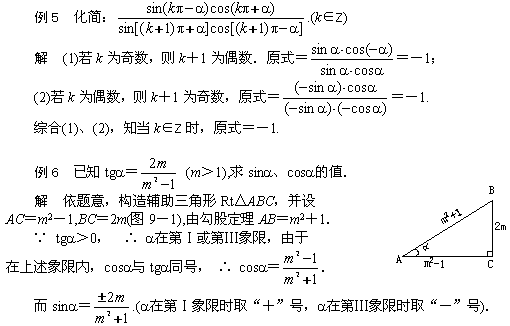 
6. 三角函数的图象、单位图以及三角函数线，为我们提供了数形结合的解题方法，在解题中有着广泛的应用，应引起足够的重视．
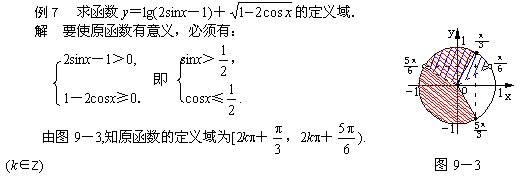
7. 在函数y＝Asin(ωx＋j)＋k (A＞0, ω＞0)中，A和ω确定函数图象的形状，j和k确定图象的位置．
作函数y＝Asin(ωx＋j)＋k的图象，既可用“五点法”，也可用图象变换的方法．图象的基本变换有振幅变换、周期变换，以及相位变换（左、右平移）和上下平移，前两种变换是伸缩变换，后两种变换是平移变换．
对函数y＝Asin(ωx＋j)＋k (A＞0, ω＞0, j≠0, k≠0),其图象的基本变换有：
(1)振幅变换（纵向伸缩变换）：是由A的变化引起的．A＞1,伸长；A＜1,缩短．
(2)周期变换(横向伸缩变换)：是由ω的变化引起的．ω＞1，缩短；ω＜1,伸长．
(3)相位变换(横向平移变换)：是由φ的变化引起的．j＞0,左移；j＜0，右移．
(4)上下平移(纵向平移变换): 是由k的变化引起的．k＞0, 上移；k＜0,下移
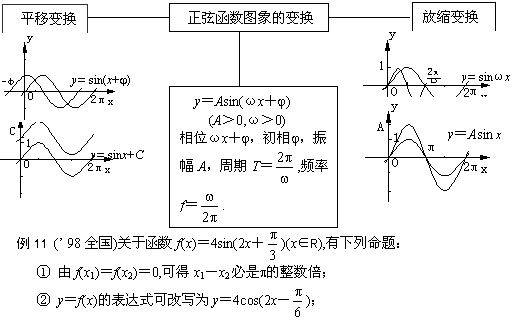
于是，本题的答案为②、③．
评析 本例所用的方法带有普遍性，用来解有关函数y＝Asin（ωx＋j）的图象是十分奏效的。
