高三数学解答题专项训练2
１．已知
．求
之值．
2．甲、乙两支篮球队进行比赛，已知每一场甲队获胜的概率为0.6，乙队获胜的概率为0.4,每场比赛均要分出胜负，比赛时采用三场两胜制，即先取得两场胜利的球队胜出．
（Ⅰ）求甲队以二比一获胜的概率；
（Ⅱ）求乙队获胜的概率；
（Ⅲ）若比赛采用五局三胜制，试问甲获胜的概率是增大还是减小，请说明理由 ．
3．若公比为C的等比数列
的首项
＝１，且满足
①求C的值；
②求数列
的前ｎ项和．
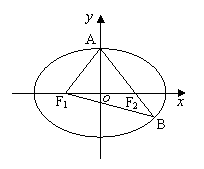4．如图，已知椭圆
，
分别为椭圆的左、右焦点，A为椭圆的上顶点，直线
交椭圆于另一点B．
（Ⅰ）若
，求椭圆的离心率；
（Ⅱ）若椭圆的焦距为2，且
，求椭圆的方程．
5.已知函数
,且
的图象经过点
,数列
为等差数列.
(1)求数列
的通项公式；
(2)当
为奇数时,设
,是否存在自然数
和
,使不等式
恒成立,若存在,求出
的最小值;若不存在,说明理由.