高考数学招生全国统一考试1

高考数学招生全国统一考试1

数　学（理工类）

一、填空题（本大题满分48分）

（1）若zÌC，且(3＋z)i=1 (i为虚数单位)，则z＝　　　　　　　　　　　　　。

（2）已知向量和的夹角为120°，且，，则＝　　　　　　　。

（3）方程 log₃(1－2·3^x)=2x＋1的解x＝　　　　　　　　　　　　　　。

（4）若正四棱锥的底面边长为cm，体积为cm³，则它的侧面与底面所成的二面角的大小是　　　　　　　　　　　　　　　　　　。

（5）在二项式(１＋３x)ⁿ和(２x＋５)ⁿ的展开式中，各项系数之和分别记为a_n、b_n、n

是正整数，则＝　　　　　　　　　　　　。

（6）已知圆x_­­²＋(y－1)²=1和圆外一点p（－2,0）,过点P作圆的切线，则两条切线夹角的正切值是　　　　　　　　　　　　　　　　　　。

（7）在某次花样滑冰比赛中，发生裁判受贿事件，竞赛委员会决定将裁判曰原来的９名增至14名，但只任取其中７名裁判的评分作为有效分，若14名裁判中有2人受贿，则有效分中没有受贿裁判的评分的概率是　　　　　　　　　　　　。（结果用数值表示）

（8）曲线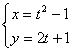(t为参数)的焦点坐标是　　　　　　　　　　　　　。

（9）若A、B两点的极坐标为，B(6，0)，则AB中点的极坐标是_________(极角用反三角函数值表示)

（10）设函数f（x）＝sin2x，若f（x＋t）是偶函数，则t的一个可能值是　　　　　　　。

（11）若数列｛a_n｝中，a₁＝３，且（n是正整数），则数列的通项a_n＝　　　　。

（12）已知函数y＝f（x）（定义域为D，值域为A）有反函数y＝f^-－１（x），则方程f（x）＝０有解x＝a，且f（x）＞x（x∈Ｄ）的充要条件是y＝f^-－１（x）满足　　　　　　　．

二、选择题（本大题满分16分）

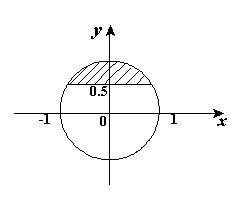
（13）如图，与复平面中的阴影部分（含边界）对应的复数集合是

（Ａ）.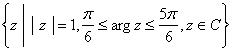

（Ｂ）.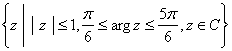

（Ｃ）.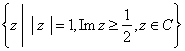

（Ｄ）.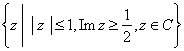　

（14）已知直线l、m，平面a 、b ，且l⊥a ，mÌb ，给出下列四个命题；

（１）若a ∥ b ，则l⊥m .　　　　  （２）若l⊥m ，则a ∥ b.　

（３）若a ⊥ b ，则l∥m .　　　　　（４）若l∥m ，则a ⊥ b.　

其中正确命题的个数是

（Ａ）１个.　　　（Ｂ）２个.　　　（Ｃ）３个.　　　（Ｄ）４个.

（15）函数y＝x＋sin x ，x∈[－p，p]的大致图象是

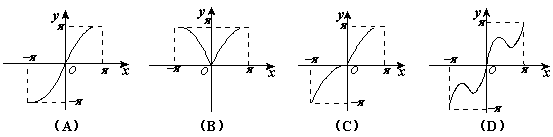
（16）一般地，家庭用电量（千瓦时）与气温（℃）有一定的关系，图（１）表示某年12个月中每月的平均气温，图（２）表示某家庭在这年12个月中每月的用电量，根据这些信息，以下关于该家庭用电量与气温间关系的叙述中，正确的是

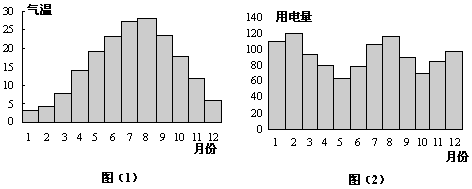　（Ａ）气温最高时，用电量最多.

　（Ｂ）气温最低时，用电量最少.

　（Ｃ）当气温大于某一值时，用电量随气温增高而增加.

　（Ｄ）当气温小于某一值时，用电量随气温降低而增加.

三、解答题（本大题满分86分）本大题共有6题，解答下列各题必须写出必要的步骤。

（17）（本题满分12分）

如图，在直－棱柱ABO－A¢B¢O¢中，OO ¢= 4，OA = 4 , OB = 3 , ∠AOB＝90°，D是线段A¢B¢的中点，P是侧棱BB¢上的一点，若OP⊥BD，求OP与底面AOB所成角的大小（结果用反三角函数值表示）

（18）（本题满分12分）

已知点A和B，动点A、B两点的距离之差的绝对值为2，点C的轨迹与直线y＝x－２交于D、E两点，求线段DE的长.

（19）（本题满分14分）本题共有２个小题，第1小题满分６分，第２小题满分８分.

已知函数f（x）＝x² ＋2x·tanθ－1，.

（１）当时，求函数f（x）的最大值与最小值;

（２）求θ的取值范围，使y＝f(x)在区间上是单调函数.

（20）（本题满分14分）本题共有２个小题，第１小题满分４分，第２小题满分10分。

某商场在促销期间规定：商场内所有商品按标价的80%出售，同时，当顾客在该商场内消费满一定金额后，按如下方案获得相应金额的奖券：

　

根据上述促销方法，顾客在该商场购物可以获得双重优惠，例如，购买标价为400元的商品，则消费金额为320元，获得的优惠额为：400×0.2＋30＝110（元），设购买商品得到的优惠率＝，试问：

（１）若购买一件标价为1000元的商品，顾客得到的优惠率是多少？

（２）对于标价在[500，800]（元）内的商品，顾客购买标价为多少元的商品，可得到不小于的优惠率？

（21）（本题满分16分）本题共有3个小题，第１小题满分４分，第２小题满分６分，第３小题满分６分）.

已知函数f(x)＝a·b^x的图象过点A（4、）和B（5，1）.

（１）求函数f(x)的解析式；

（２）记a_n＝log₂ f(n)、n是正整数，S_n是数列｛a_n｝的前n项和，解关于n的不等式a_nS_n≤0；

（３）对于（２）中的a_n与S_n，整数10⁴是否为数列｛a_nS_n｝中的项？若是，则求出相应的项数；若不是，则说明理由。

（22）（本题满分18分）本题共有3个小题，第１小题满分４分，第２小题满分６分，第３小题满分８分）。

规定，其中x∈R，m是正整数，且，这是组合数（n、m是正整数，且m≤n）的一种推广。

⑴ 求的值；

⑵组合数的两个性质：①＝；② ＋＝．是否都能推广到（x∈R，m是正整数）的情形？若能推广，则写出推广的形式并给出证明；若不能，则说明理由；

　　 ⑶ 已知组合数是正整数，证明：当x∈Z，m是正整数时，∈Z．

　

普通高等学校招生全国统一考试1

数学参考答案（理工类）

一、（第１题至第１２题）

（1）　 –3－i .　　（2）　13 .　　　（3） –1 .　　　 （4） 30°

（5）  .　　 （6）  .

（7）　　.　　（8）（0.1）.　 （9）.　　　　　

 （10）　 .　　（11）  .

（12） f^-－１(０)＝a，且f^-－１(x)＜ x （x∈Ａ）/ y＝f^-－１(x)的图象在直线y＝x的下方，且与y轴的交点为（０, a）/……

二、（第13题至第16题）

（13）D　　 （14）B　　 （15）C　　  （16）C　　

三、（第17题至第22题）

（17）　[解法一]如图，以O点为原点建立空间直角坐标系.

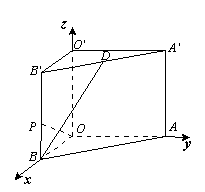由题意，有B（3，0，0），.

设P（3，0，z），则

，.

∵BD⊥OP , ∴ .

.

∵BB¢⊥平面AOB，∴　∠POB是OP与底面AOB所成的角.

　　，∴.

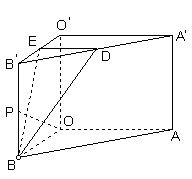
[解法二]取O¢B¢中点E，连结DE、BE，则

　　DE⊥平面OB B¢ O¢.

　　∴　BE是BD在平面OB B¢ O¢内的射影.

　　又∵　OP⊥BD .

由三垂线定理，得　 OP⊥BE  .

在矩形OB B¢ O¢中，易得Rt△OBP ∽ Rt△B B¢ E .

∴ 　,　得　 .

　 （以下同解法一）

（18）[解]设点C（x , y）,　则　｜CA －｜CB ＝±２.

根据双曲线的定义，可知点C的轨迹是双曲线

　　　　　　　.

　由　2a ＝２，，得a²＝１，b²＝２.

故点C的轨迹方程是.

由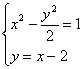，得　x²＋4x－６＝０.

∵　△＞０，∴　直线与双曲线有两个交点.

设D（x₁，y₁）、E（x₂，y₂），则　x₁＋x₂＝－４，x₁·x₂＝－6.

故.

（19）　[解]（1）当时，，，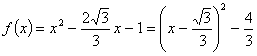　

  ∴　时，f(x) 的最小值为.

　　x＝－1时，f(x)的最大值为.

　（２）函数f(x)＝(x＋tanθ)²－1－tan²θ图象的对称轴为x＝－tanθ.

∵　y＝f(x)在区间上是单调函数.

∴　－tanθ≤－1　或　－tanθ≥　，

即 tanθ≥1　或　tanθ≤－　，

因此θ的取值范围是.

（20） [解]（１）　.

　　　　　（２）设商品的标价为x元.

　　　　　 则500 ≤ x ≤ 800 ,消费额：４00 ≤ 0.8x ≤ 640　.

　　由已知得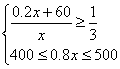（Ⅰ）　　或　（Ⅱ）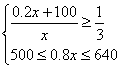

　　　　不等式组（Ⅰ）无解，不等式组（Ⅱ）的解为625≤x≤750 .

因此，当顾客购买标价在[625,750]元内的商品时，可得到不小于的优惠率.

（21）　[解]（１）由，1＝a·b⁵，得b＝4，.

故.

　　（２）由题意.

　　　，a_nS_n＝2n（n－5）（n－9）.

　　  由a_nS_n≤0，得（n－5）（n－9）≤0，即　5≤n≤9.

　　  故　n＝5，6，7，8，9.

　　（３）a_１S_１＝64 ,　 a_２S_２＝84 ,　 a_３S_３＝72 ,　 a_４S_４＝40 .

　　　当5≤n≤9时，a_nS_n≤0.

　　　当10≤n≤22时，a_nS_n≤a₂₂S₂₂＝9724＜10⁴ .

　　　当n≥23时，a_nS_n≥a₂₃S₂₃＝11592＞10⁴ .

因此，10⁴不是数列｛a_nS_n｝中的项.

（22）[解] （1）＝＝－11628；

　　　　（2）＝不能推广到的情形，例如，无意义；

　　　　　  ＋＝．能推广到的情形，

　　　　　　  ＋＝

　　　　　　　　 ＝

　　　　　　　　 ＝

　　　　　　　　 ＝＝．

　　　　 （3）① 当0≤x＜m时，中一定有一个为零，＝0；

　 　　　　② 当x≥m时，是组合数，∈Z；

　　　　　 ③ 当x＜0时，＝

　　　　　　　　 ＝

　　　　　　　　 ＝

　　　　　　　　 ＝∈Z．