高三理科数学作业(一)
一、选择题 班级_________________姓名_________________
1．在数列
则此数列的前4项之和为 （ ）
A．0 B．1 C．2 D．－2
2．函数
的值域是 （ ）
A．
B．
C．
D．
3．若函数
= （ ）
A．
B．－ C．－2 D．2
4．若函数
的表达式是 （ ）
A．
B．
C．
D．
5．等差数列{an}的首项a1=1，公差d≠0，如果a1，a2，a5成等比数列，那么d= （ ）
|
6．已知
为互相垂直的单位向量，
的夹角为锐角，则实数
的取值范围是 A． 
B．
C.
D．
（ ）
7．已知
，
满足的关系是
（ ）
A．
B．
C.
D．
8．下列命题中错误的是 （ ）
A．命题“若q则p”与命题“若
p则q”互为逆否命题
B．“am2<bm2”是“a<b”的充要条件
C．“矩形的两条对角线相等”的否定为假
|
{1，2}或4
{1，2}”为真（其中为空集）
9．设△ABC的两个内角A，B所对的边分别为a , b，复数
若复数z1·z2在复平面上对应的点在虚轴上，则△ABC是 （ ）
A．等腰三角形或直角三角形 B．等腰直角三角形
C．等腰三角形 D．直角三角形
10．设
为坐标平面内一点，O为坐标原点，记f(x)=
，当x变化时，函数 f(x)的最小正周期是 （ ）
A．30π B．15π C．30 D．15
二、填空题：
11．记Tn=a1·a2·…·an(n∈N*)表示n个数的积，其中ai为数列{an}中的第i项，若an=2n－1,T4= .
12．若向量a,b是非零向量，则“a·b<0”是“向量a,b的夹角为钝角”的 条件.
13．函数
的单调递增区间是
.
14．设函数
是定义在
上以3为周期的奇函数，若
，
，则
的取值范围是________.
三、解答题：
15．设△ABC的内角A，B，C成等差数列，且满足条件
试判断△ABC的形状，并证明你的结论.
16．已知命题
：复数
对应的点落在复平面的第二象限；命题
：以
为首项，公比为
的等比数列的前
项和极限为2.若命题“且”是假命题，“或”是真命题，求实数的取值范围.
17. 已知二次函数f(x)(x∈R)的二次项系数为正实数且满足
（Ⅰ）试判断函数f(x)的单调区间；
（Ⅱ）设向量a=(sinx，2)，b=(2sinx，)，c=（cos2x，1），d=（1，2）.求解不等式 f(a·b)>f(c·d).
18．已知数列
（1）求数列{an}的通项公式；（2）求数列{bn}的通项公式；（3）求数列{bn}的前n项和Tn.
元旦作业（一）参考答案
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | D | D | B | A | B | D | B | A | D |
二、填空题：
11.105 12.必要不充分 13. 
14. 
二、解答题：
15．
16．解：命题有：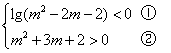
由①得：
由②得：
由上得满足P的m的取值范围是：
或 
对命题,有：
又
得：
且
又命题“且”是假命题，“或”是真命题，则m的范围是 
17解：（I）设
∴f(x)得单调递增区间为
，单调递减区间为
.
（II）依题意有a·b=2sin2x+1≥1, c·d=cos2x+2=1+2cos2x≥1. 依题意f(a·b)>f(c·d)，
∴2sin2x+1>2cos2x+1
sin2x>cos2xcos2x<0 ∴
18. 
或者用累乘得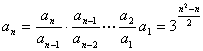
