高三摸底考试理科数学
(必修+选修Ⅱ)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试用时120分.
第Ⅰ卷(共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、考号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮
擦干净后,再选涂其他答案标号。不能答在试题卷上。
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A)·P(B)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,选择一个符合题目要求的选项。
1.设P、Q为两个非空实数集合,定义集合![]() ,若P={-1,0,1},Q={-2,2},则集合
,若P={-1,0,1},Q={-2,2},则集合![]() 中元素的个数是
中元素的个数是
A.3 B.4 C.5 D.6
2.已知![]() ,其中m,n是实数,是m+ni等于
,其中m,n是实数,是m+ni等于
A.1+2i B.1-2i C.2+i D.2-i
3.若![]() 则下列不等式:①
则下列不等式:①![]() ②
②![]() ③
③![]() ④
④![]() 中,正确的不等式有
中,正确的不等式有
A.①② B.②③ C.①④ D.③④
4.若![]() ,则
,则![]() 的值是
的值是
A.![]() B.
B.![]() C.-
C.-![]() D.-
D.-![]()
5.若数列{an}满足![]() ,则a2007的值
,则a2007的值
A.1 B.-1 C.![]() D.2
D.2
6.已知![]() ,点C在∠AOB内,且∠AOC=45°,设
,点C在∠AOB内,且∠AOC=45°,设![]() ,则
,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
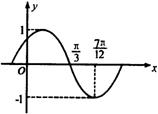 7.把函数
7.把函数![]() 的图象按向量
的图象按向量![]() 平移,所得曲线的一部分如图所示,则ω,
平移,所得曲线的一部分如图所示,则ω,![]() 的值分别是
的值分别是
A.1,![]() B.1,-
B.1,-![]()
C.2,![]() D.2,-
D.2,-![]()
8.已知向量![]() 、
、![]() 满足
满足![]() 等于
等于
A.2 B.![]() C.
C.![]() D.
D.![]()
9.已知实数a,b满足等式![]() ,下列五个关系式:①1<a<b;②1<b< a;③b<
a<1;④a<b<1;⑤a=b,其中不可能成立的关系有
,下列五个关系式:①1<a<b;②1<b< a;③b<
a<1;④a<b<1;⑤a=b,其中不可能成立的关系有
A.4 B.3 C.2 D.1
10.下列函数既是奇函数,又在区间[-1,1]上单调递减的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.在△OAB中,O为坐标原点,![]() ,其中
,其中![]() ,则当△OAB的面积达到最小值时,θ的值
,则当△OAB的面积达到最小值时,θ的值
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.同时满足条件:①函数图象成中心对称图形;②对任意a、b![]() [0,1],若
[0,1],若![]() ,有
,有![]() 的函数是
的函数是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
第Ⅱ卷(共90分)
注意事项:
1.用钢笔或圆珠笔直接答在试题卷中。
2.答卷前将密封线内的项目填写清楚。
二、填空题:本大题共4小题,每小题4分,共16分.答案须填在题中横线上.
13.已知![]() 的夹角45°,要使
的夹角45°,要使![]() 垂直,则λ= .
垂直,则λ= .
14.各项都是正数的等比数列{an}的公比![]() ,且
,且![]() 成等差数列,则
成等差数列,则![]() 的值是
.
的值是
.
15.某公司租地建仓库,每月土地占用费y1与仓库到车站的距离成反比,而每月库存货物的运费y2与到车站的距离成正比,如果在距离车站10千米处建仓库,这两项费用y1和y2分别为2万元和8万元.那么,要使这两项费用之和最小,仓库应建在离车站 千米处.
16.数列![]() 是正项等差数列,若
是正项等差数列,若![]() ,则数列
,则数列![]() 也为等差数列. 类比上述结论,写出正项等比数列
也为等差数列. 类比上述结论,写出正项等比数列![]() ,若
,若![]() =
, 则数列{
=
, 则数列{![]() }也为等比数列.
}也为等比数列.
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
在△ABC中,角A、B、C的所对边分别为a、b、c,已知![]() ,且最长边边长为1. 求:
,且最长边边长为1. 求:
(1)角C的大小;
(2)△ABC最短边的长.
18.(本小题满分12分)
已知向量![]() ,定义函数
,定义函数![]()
![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)求函数![]() 的最大值或最小值及此时对应的x的值;
的最大值或最小值及此时对应的x的值;
(3)确定函数![]() 的单调递增区间.
的单调递增区间.
19.(本小题满分12分)
设数列{an}、{bn}满足:![]() ,且数列
,且数列![]()
![]() 是等差数列,{bn-2}是等比数列。
是等差数列,{bn-2}是等比数列。
(1)求数列{an}和{bn}的通项公式;
(2)是否存在![]() ,使
,使![]() ,若存在,求出k;若不存在,说明理由.
,若存在,求出k;若不存在,说明理由.
20.(本小题满分12分)
某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(最大供应量)如下表所示:
|
资源 | 甲产品 (每吨) | 乙产品 (每吨) | 资源限额 (每天) |
| 煤(t) | 9 | 4 | 360 |
| 电力(kw·h) | 4 | 5 | 200 |
| 劳力(个) | 3 | 10 | 300 |
| 利润(万元) | 7 | 12 |
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
21.(本小题满分12分)
已知![]() ,设P:
,设P:![]() 和
和![]() 是方程
是方程![]() 的两个根,不等式
的两个根,不等式![]() 对任意实数
对任意实数![]() 恒成立:Q:函数
恒成立:Q:函数![]() -∞,∞)上有极值.求使“P且Q”为真命题的m的取值范围.
-∞,∞)上有极值.求使“P且Q”为真命题的m的取值范围.
22.(本小题满分14分)
已知函数![]()
(1)证明:存在![]() ,使
,使![]() ;
;
(2)设![]() 其中n=1,2,…,证明:
其中n=1,2,…,证明:![]() ;
;
(3)证明:![]()
参考答案
一、选择题:
1—5:ACCCB 6—10:CDACD 11—12:BC
二、填空题:
13.2 14.![]() 15.5
16.
15.5
16. ![]()
三、解答题:
17.(1)![]() ……………………(2分)
……………………(2分)
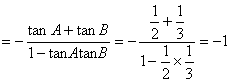 ……………………(4分)
……………………(4分)
![]() ……………………………………………………………………(5分)
……………………………………………………………………(5分)
(2)![]() 、B均为锐角且B<A
、B均为锐角且B<A
又C为钝角
∴最短边为b……………………………………………………(7分)
由![]() ,解得
,解得![]() ………………………………(9分)
………………………………(9分)
又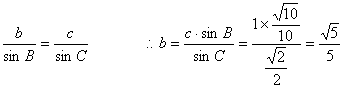 ……………(12分)
……………(12分)
18.(1)![]()
![]()
![]() ………………………………(3分)
………………………………(3分)
故![]() …………………………………………………(4分)
…………………………………………………(4分)
(2)令![]() .
.
若![]() 时,当
时,当![]() 时,函数
时,函数
![]() …………………………………………………………(6分)
…………………………………………………………(6分)
若![]() 时,当
时,当![]() 时,函数
时,函数
![]() …………………………………………………………(8分)
…………………………………………………………(8分)
(3)由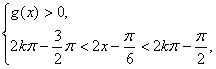
确定![]() 单调递增的正值区间是
单调递增的正值区间是![]() ;
;
由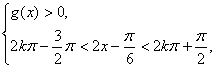
确定![]() 单调递减的正值区间是
单调递减的正值区间是![]() ;………(10分)
;………(10分)
综上,当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() .
.
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() .……(12分)
.……(12分)
注:①![]()
![]() 的这些等价形式中,以
的这些等价形式中,以![]() 最好用. 因为复合函数
最好用. 因为复合函数![]() 的中间变量
的中间变量![]() 是增函数,对求
是增函数,对求![]() 的单调区间来说,只看外层函数
的单调区间来说,只看外层函数![]() 的单调性即可.否则,利用
的单调性即可.否则,利用![]() 的其它形式,例如
的其它形式,例如![]() 求单调区间是非常容易出错的. 同学们可以尝试做一下
求单调区间是非常容易出错的. 同学们可以尝试做一下![]() 的其它形式,认真体会,比较优劣!
的其它形式,认真体会,比较优劣!
②今后遇到求类似![]() 的单调区间问题,应首先通过诱导公式将
的单调区间问题,应首先通过诱导公式将![]() 转化为标准形式:
转化为标准形式:![]() (其中A>0,ω>0),然后再行求解,保险系数就大了.
(其中A>0,ω>0),然后再行求解,保险系数就大了.
19.(1)由已知![]() ……………………(1分)
……………………(1分)
![]() …………(3分)
…………(3分)
由已知![]()
∴公差d=1…………………………………………………………(4分)
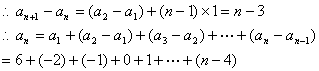
![]() ……………………………………………………(6分)
……………………………………………………(6分)
(2)设![]() …………………………(7分)
…………………………(7分)
当![]() 时,
时,![]() 是k的增函数,-
是k的增函数,-![]() 也是k的增函数.
也是k的增函数.
![]() ………………………………(10分)
………………………………(10分)
又![]()
![]() 不存在
不存在![]() ,使
,使![]() …………………………………(12分)
…………………………………(12分)
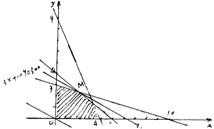
20.设此工厂应分别生产甲、乙两种产品x吨、y吨,获得利润z万元…………(1分)
依题意可得约束条件:
|
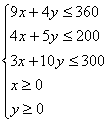 ……(4分)
……(2分)
……(4分)
……(2分)
利润目标函数![]() …………(7分)
…………(7分)
如图,作出可行域,作直线![]() ,把直线l向右上方平移至l1位置,直线经过可行域上的点M,且与原点距离最大,此时
,把直线l向右上方平移至l1位置,直线经过可行域上的点M,且与原点距离最大,此时![]() 取最大值.…………(10分)
取最大值.…………(10分)
解方程组![]() ,得M(20,24)
,得M(20,24)
故,生产甲种产品20t,乙种产品24 t,才能使此工厂获得最大利润.…………(12分)
21.由题设![]()
![]()
当![]() 时,
时,![]() 的最小值为3.
的最小值为3.
要使![]() 恒成立
恒成立
只须![]() ≤3
≤3
即2≤m≤8……………………………………………………(3分)
由已知,得![]()
此一元二次方程的判断式![]() ………(5分)
………(5分)
若![]() ,则
,则![]() 有两个相等的实根
有两个相等的实根![]() ,且
,且![]() 的符号如下:
的符号如下:
| x |
|
| ( |
|
| + | 0 | + |
因此,![]() 不是函数
不是函数![]() 的极值……………………………………(7分)
的极值……………………………………(7分)
若![]() ,则
,则![]() =0有两个不等的实根
=0有两个不等的实根![]() 和
和![]() ,且
,且![]() 的符号如下:
的符号如下:
| x |
|
| ( |
| ( |
|
| + | 0 | - | 0 | + |
因此,函数![]() 在
在![]() 处取得极大值,在
处取得极大值,在![]() 处取得极小值。……9分
处取得极小值。……9分
综上所述,当且仅当△>0时,函数![]() 在(-∞,+∞)上有极值。
在(-∞,+∞)上有极值。
由△=4m2-12m-16>0,得m<-1或m>4
即当m<-1或m>4时,Q正确 ……………………11分
综上,当![]() 时,命题“P且Q”为真命题。 ………………12分
时,命题“P且Q”为真命题。 ………………12分
22.(1)令![]()
又![]() 上连续,所以存在
上连续,所以存在![]() ……(4分)
……(4分)
(2)∵![]()
∴![]() 是R上的单调增函数
……………………5分
是R上的单调增函数
……………………5分
∴![]()
又![]() 是增函数,∴
是增函数,∴![]() …………6分
…………6分
又![]() …………7分
…………7分
综上,![]()
用数学归纳法证明如下:
①当n=1时,上面已证明成立;
②假设当n=k(k≥1)时,有![]()
当n=k+1时,由![]() 是单调递增函数,有
是单调递增函数,有![]()
即![]()
由①和②,对一切n=1,2,…,都有 ![]() ……10分
……10分
(3)方法一:
∵![]() , ∴
, ∴![]() ……11分
……11分
∴![]()
![]() ,
,
即 ![]() ………………14分
………………14分
方法二:∵![]() , ∴
, ∴![]() ………………11分
………………11分
∴![]()
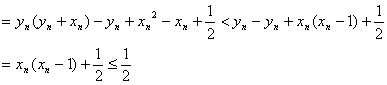
即 ![]() ……………………14分
……………………14分
 产品
产品