高三年级阶段测试数学试卷（二）
第一卷（选择题共50分）
一、 选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题意要求的。
1． 已知集合
,则
A. 
B. 
C. 
D. 
2. 下列函数中,在区间
上为减函数的是:
A. 
B. 
C. 
D. 
3．在等比数列
中，
，
，则
等于：
A. 
或
B. 
或
C. D.
4．函数
的图像关于：
A. 
轴对称
B. 
轴对称
C. 直线
对称
D. 原点对称
5．等差数列
的通项公式是
，其前
项和为
，则数列
的前10项和为
A．75 B．70 C．120 D．100
6．函数
的反函数是：
A. 
B. 
C. 
D. 
7．对任意实数a，b，c，给出下列命题：
①“
”是“
”充要条件； ②“
是无理数”是“a是无理数”的充要条件③“a>b”是“a2>b2”的充分条件；④“a<5”是“a<3”的必要条件.
其中真命题的个数是 A．1 B．2 C．3 D．4
8．已知
，设数列满足
，
，则数列前项的和
等于：
A. 
B. 
C. 
D. 
9．函数
的图象如图，其中a、b为常数，则下列
|
A．
B．
C．
D．
10．
是定义在
上的以3为周期的奇函数，且
， 则方程
在区间
内解的个数的最小值是：
A.2 B.3 C.4 D.5
第二卷（非选择题共100分）
二、 填空题：本大题共6小题，每小题5分，共30分。把答案填在答题卷相应位置。
11．设
为实数，
成等比数列，且
成等差数列，则
的值是_________________.
12．若函数
的图象关于直线
对称，则实数
＝______________；
13．已知点
在第三象限，则角
的终边在第______________象限；
14．定义在
上的偶函数
，
是增区间，则不等式
的
解集是 ；
15．已知
且
则
；
16．
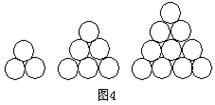在德国不莱梅举行的第48届世乒赛期间，某商场橱窗里用同样的乒乓球堆成若干准“正三棱锥”形的展品，其中第一堆只有一层，就一个乒乓球；第2、3、4、…堆最底层（第一层）分别按图4所示方式固定摆放.从第一层开始，每层的小球自然垒放在下一层之上，第n堆第n层就放一个乒乓球，以
表示第n堆的乒乓球总数，则
；
（答案用n表示） .
三、解答题：本大题共5题，每题14分，共30分。解答应写出文字说明、证明过程或演算步骤
17．记函数f(x)＝lg(2x－3)的定义域为集合M，函数g(x)＝
的定义域为集合N.
求⑴集合M，N；⑵集合M
N，M
N.
18．数列
的前三项为1，3，6，它是由一个等比数列
和一个首项为零的等差数列
的对应项相加而得到.
⑴求、的通项公式；
⑵求数列的前n项和Sn ；
⑶是否存在自然数n，使得
>
成立？如果存在，求出n的值；如果不存在，试说
明现由.
19．已知函数
.
⑴若当x
[1，2]时，
有意义，求实数的取值范围；
⑵若不等式
在区间[1，2]上恒成立，求实数的取值范围.
20．某地区发生流行性病毒感染，居住在该地区的居民必须服用一种药物预防，规定每人
每天早晚八时各服一片，现知该药片每片含药量为220毫克，若人的肾脏每12小时
从体内滤出这种药的60%，如果在体内的残留量超过386毫克，就将产生副作用.
⑴某人上午8时第一次服药，问到第二天上午八时服完药时，这种药在他体内还残留
多少？
⑵第n次服药后，药在人体内的残留量有多少？
（3）长期服用的人这种药会不会产生副作用？
21．数列的前n项和
(nN * )，且
＝1，
(nN *).
⑴求数列的通项；
⑵已知定理：“若函数f(x)在区间D上是凹函数，x>y (x，yD)，且
存在，则有
”. 若函数y＝x n＋1(nN *)，在(0，+
)上是凹函数，试判断
bn与bn＋1的大小；
⑶求证：≤bn<2.
答案：一。C,D,B,D,A, B,B,C,D,D,
二．11．2.5 12。-2 13。 二
14。
15。0
16。10，