高三年级数学11月周考试题
(理科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至6页,卷面共150分,考试时间120分钟.
第Ⅰ 卷(选择题 共60分)
注意事项: 1.答第Ⅰ卷前,考生务必将自己的准考证号、试场号用钢笔或圆珠笔填写在答题卷上. 2.每小题选出答案后,用钢笔或圆珠笔填写在答题卷上.
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、已知集合![]() ,
,![]() ,则
,则![]() 为
为
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
2、若不等式ax2+bx+2![]() 的解集为(-
的解集为(-![]() ,
,![]() ),则a+b的值是
),则a+b的值是
A.10 B.-10 C.14 D.-14
3、已知集合M=![]() ,集合N=
,集合N=![]() ,若N
,若N![]() M则a的值是( )
M则a的值是( )
A.1 B.-1 C. 1或-1 D. 0或1或-1
4.设复数![]() (
(![]() 、
、![]() )满足
)满足![]() ,那么复数
,那么复数![]() 在复平面内对应的点位于
在复平面内对应的点位于
A.第一、二象限 B.第一、三象限 C.第一、四象限 D.第二、四象限
5、已知直线![]() ,直线
,直线![]() ,则“
,则“![]() ”是“直线
”是“直线![]() ”的
”的
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
6、用反证法证明命题:“a,b∈N,ab可被5整除,那么a,b中至少有一个能被
5整除”时,假设的内容应为( )
A. a,b都能被5整除 B. a,b都不能被5整除
C. a,b不都能被5整除 D. a不能被5整除
7.下列函数既是奇函数,又在区间![]() 上单调递减的是
上单调递减的是
A![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、设![]() 表示平面,
表示平面,![]() 表示直线,给定下列四个命题:
表示直线,给定下列四个命题:
①![]() ;②
;②![]() ;
;
③![]() ;④
;④![]() .其中正确命题的个数有
.其中正确命题的个数有
A、1个 B、2个 C、3个 D、4个
9、已知![]() 的值为
的值为
A.-2 B.-1 C.1 D.0
10、函数![]()
![]() 的定义域是
的定义域是
![]() A. [1,+
A. [1,+![]() ]
] ![]() B .(
B .(![]() ,1] C.(
,1] C.(![]() ) D.(-
) D.(-![]() ]
]
11、若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为![]() ,值域为
,值域为![]() 的“同族函数”共有
的“同族函数”共有
A.9个 B.8个 C.5个 D.4个
12.在同一平面直角坐标系中,函数![]() 和
和![]() 的图象关于直线
的图象关于直线![]() 对称. 现将
对称. 现将![]() 的图象沿
的图象沿![]() 轴向左平移2个单位,再沿
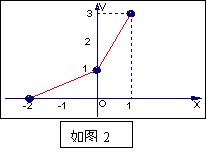
轴向左平移2个单位,再沿![]() 轴向上平移1个单位,所得的图象是由两条线段组成的折线(如图2所示),则函数
轴向上平移1个单位,所得的图象是由两条线段组成的折线(如图2所示),则函数![]() 的表达式为
的表达式为
 A.
A.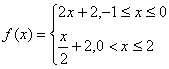
B.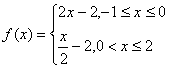
C.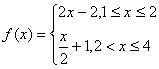 D.
D.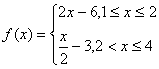
第Ⅱ 卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在题中相应的横线上。
13、复数![]() 的值是 。
的值是 。
14、设等差数列![]() 的公差
的公差![]() 0,又
0,又![]() 成等比数列,则
成等比数列,则![]() 。
。
15、函数![]()
![]() 的反函数是___________________
的反函数是___________________
16、以下同个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数,![]() ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②设定圆C上一定点A作圆的动点弦AB,O为坐标原点,若![]() 则动点P的轨迹为椭圆;
则动点P的轨迹为椭圆;
③方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线![]() 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
三.解答题:本大题共6小题,共84分.解答应写出文字说明,证明过程或演算步骤.
17、(12分)已知集合![]() ,C={xx2+
,C={xx2+![]() }.
}. ![]()
![]() (1)若
(1)若![]() =A,求实数
=A,求实数![]() 的取值范围; (2)
的取值范围; (2)![]() ,且
,且![]() ,求
,求![]() 、
、![]() 的值.
的值.
(18)(12分)设函数f(x)=![]() ,其中向量
,其中向量![]() =(2cosx,1),
=(2cosx,1),![]() =(cosx,
=(cosx,![]() sin2x),x
sin2x),x![]() R.
R.
(1)若f(x)=1-![]() 且x
且x![]() [-
[-![]() ,
,![]() ],求x;(2)若函数y=2sin2x的图象按向量
],求x;(2)若函数y=2sin2x的图象按向量![]() =(m,n)(
=(m,n)(![]() <
<![]() )平移后得到函数y=f(x)的图象,求实数m,n的值。
)平移后得到函数y=f(x)的图象,求实数m,n的值。
19、(12分)甲、乙、丙三人在同一办公室工作。办公室只有一部电话机,设经过该机打进的电话是打给甲、乙、丙的概率依次为![]() 、
、![]() 、
、![]() 。若在一段时间内打进三个电话,且各个电话相互独立。求:(Ⅰ)这三个电话是打给同一个人的概率;(Ⅱ)这三个电话中至少有两个是打给甲的概率;
。若在一段时间内打进三个电话,且各个电话相互独立。求:(Ⅰ)这三个电话是打给同一个人的概率;(Ⅱ)这三个电话中至少有两个是打给甲的概率;
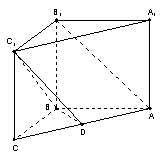 20、(12分)如图所示,在直三棱柱
20、(12分)如图所示,在直三棱柱![]() 中,
中,![]() ,
,![]() 为棱
为棱![]() 的中点,且
的中点,且![]()
![]() 。
。
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求异面直线![]() 与
与![]() 所成的角;
所成的角;
21. (12分)设命题P:关于x的不等式![]() 的解集为R。命题Q:函数
的解集为R。命题Q:函数![]() 的定义域为R. 若命题“
的定义域为R. 若命题“![]() 且
且![]() ”是假命题,“
”是假命题,“![]() 或
或![]() ”是真命题,求实数a的取值范围.
”是真命题,求实数a的取值范围.
22(14分)函数![]() 是定义域为R的偶函数,且对任意的
是定义域为R的偶函数,且对任意的![]() ,均有
,均有![]() 成立.当
成立.当![]() 时,
时,![]()
(1)当![]() 时,求
时,求![]() 的表达式;
的表达式;
(2)若![]() 的最大值为
的最大值为![]() ,解关于x的不等式
,解关于x的不等式![]() .
.