高三年级数学月考测试(三)
一、 填空题:(每小题4分,共48分)
1.
若函数![]() 的反函数的图像经过点
的反函数的图像经过点![]() ,则
,则![]()
2.
设全集![]() ,则
,则![]()
3.
函数![]() 的图像位于
的图像位于![]() 轴右侧的对称轴从左到右分别为
轴右侧的对称轴从左到右分别为![]() ,则
,则![]() 的方程为
的方程为
4. 如右图的程序图像中,输出的结果为
5.
若数列![]() 的前n项和为
的前n项和为![]() ,通项公式
,通项公式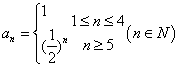 ,则
,则![]()
6.
已知![]() 方程的解是
方程的解是
7. 甲、乙、丙3人相互传球,由甲作第一次传球,则经过2次传球后求在丙手中的概率为
8.
若函数![]() 在区间
在区间![]() 上存在反函数,则示数
上存在反函数,则示数![]() 的取值范围是
的取值范围是
9.
已知函数![]() 是奇函数,则
是奇函数,则![]()
10.
若![]() ,则
,则![]() 的形状是
的形状是
11.
函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为
12.
对于实数![]() ,若
,若![]() ,规定
,规定![]() ,如果定义函数
,如果定义函数![]() ,那么下列命题正确的是
。(填所有正确命题的序号)
,那么下列命题正确的是
。(填所有正确命题的序号)
(1)函数![]() 的定义域为R
(2)函数
的定义域为R
(2)函数![]() 的值域为
的值域为![]()
(3)方程![]() 有实数解 (4)函数
有实数解 (4)函数![]() 是周期函数
是周期函数
(5)函数![]() 是增函数
(6)函数
是增函数
(6)函数![]() 的图像关于
的图像关于![]() 对称
对称
二、 选择题;(每小题4分,共16分)
13.等差数列![]() 中,
中,![]() ,前
,前![]() 项和为
项和为![]() ,若
,若![]() ,则数列
,则数列![]() 中最大项是( )
中最大项是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
14.在![]() 中,若
中,若![]() ,那么
,那么![]() 中必然有一个角是( )
中必然有一个角是( )
(A) ![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
15。一个数列![]() ,某人仅看到其中三项:
,某人仅看到其中三项:![]() ,以上说法正确的是( )
,以上说法正确的是( )
(A)此数列一定不是等差数列,也一定不是等比数列
(B)次数列可能是等差数列,但一定不是等比数列
(C)次数列一定不是等差数列,但可能是等比数列
(D)次数列可能是等差数列,也可能是等比数列
16.设定义域为![]() 的函数
的函数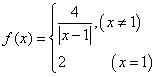 ,若关于
,若关于![]() 的方程
的方程![]() 有三个不同的实数解
有三个不同的实数解![]() ,则
,则![]() 等于(
)
等于(
)
(A)3
(B) 9
(C)![]() (D) 11
(D) 11
三、 解答题:(本大题满分86分)
17.求函数
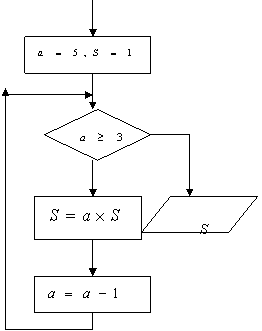
![]() 的最小正周期和值域,并写出
的最小正周期和值域,并写出![]() 取得最大值时的
取得最大值时的![]() 的值。(本题12分)
的值。(本题12分)
18.(本大题12分)解关于![]() 的不等式
的不等式![]()
19.(本题14分)数列![]() 中,
中,![]() ,且满足
,且满足![]()
![]() 。
。
(1)求数列![]() 的通项公式;(6分)
的通项公式;(6分)
(2)设![]() 。(8分)
。(8分)
20.(本题14分)
某商场在促销期间规定:商场内所有商品按标价的80%出售;同时,当顾客在该商场消费满一定金额后,按如下方案获得相应金额的奖券;
| 消费金额(元)的范围 |
|
|
|
| … |
| 获得奖券的金额(元) | 30 | 60 | 100 | 130 | … |
根据上述促销方式,顾客在该商场购物可以获得双重优惠。例如,购买标价为400元的商品,则消费金额为320元,获得的优惠额为:![]() (元)。设购买商品得到的优惠率=
(元)。设购买商品得到的优惠率=![]() ,试问:
,试问:
(1) 购买一件标价为1000元的商品,顾客得到的优惠率是多少?(6分)
(2) 对于标价在![]() (元)的内的商品,顾客购买标价为多少元的商品,可得到不小于
(元)的内的商品,顾客购买标价为多少元的商品,可得到不小于![]() 的优惠率?(8分)
的优惠率?(8分)
21.(本大题16分)
已知函数![]() ,
,
并且![]() 。
。
(1)
求![]() 的值;(6分)
的值;(6分)
(2)
是否存在各项均不为零的数列![]() ,满足
,满足![]() 。若存在,写出数列的一个通项公式
。若存在,写出数列的一个通项公式![]() ,并说明满足条件的数列
,并说明满足条件的数列![]() 是否唯一确定;若不存在,请说明理由。
是否唯一确定;若不存在,请说明理由。
22.(本大题18分)
已知二次函数![]() 同时满足:①
同时满足:①![]() 的图像与
的图像与![]() 轴只有一个交点;②在定义域内存在
轴只有一个交点;②在定义域内存在![]() ,使得不等式
,使得不等式![]() 成立,设数列
成立,设数列![]() 的前
的前![]() 项和
项和![]() 。
。
(1)
求数列![]() 的通项公式。(4分)
的通项公式。(4分)
(2)
设各项均不为零的数列![]() 中,所有满足
中,所有满足![]() 的正整数
的正整数![]() 的个数称为这个数列的变号数,令
的个数称为这个数列的变号数,令![]() ,求数列
,求数列![]() 的变号数。(7分)
的变号数。(7分)
(3)
若![]() ,求数列
,求数列![]() 中值最大的项。(7分)
中值最大的项。(7分)