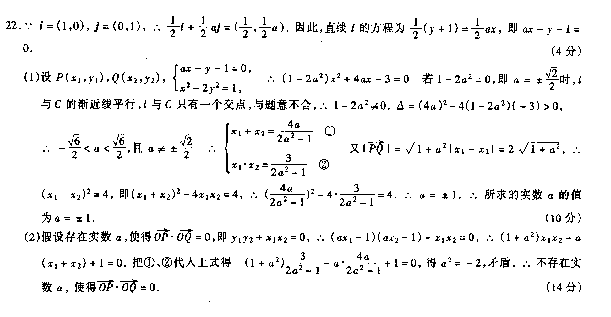高三年级质量检测数学试题
(文科) 试卷类型：A
第Ⅰ卷(选择题共60分)
说明：一、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分满分150分，考试时间为120分钟。
二、参考公式
1．如果事件A、B互斥，那么P(A+B)=P(A)+P(B)；
2．如果事件A、B相互独立，那么P(A·B)=P(A)·P(B)；
3．如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概
一、选择题(每小题5分。共12小题。共60分．)
1. 集合P={1，3，5，7，9，…，2n一1，…}(n∈N﹡)，若a∈P，b∈P，则。a+ b∈P，则运算+ 可能是
A．加法 B．减法 C．除法 D．乘法
2．袋中有红、黄、绿色球各一个，每次任取一个，有放回地抽取三次，球的颜色全相同的概率是
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分又不必要条件
4．已知数列{an}是等差数列，且a1+a2+a3=12，a4+a5+a6=18，则a7+a8 +a9等于
A．24 B．6 C．0 D．-12
5．若指数函数y=aχ(a>0且a≠1)在[-1，1]上的最大值与最小值的差是1，则底数a等于
6．定义在R上的函数y：f(x)为周期函数，最小正周期为T，若函数y=f(x)，x∈(0，T)时有反函
数y=f -1(x),x∈D，则函数y=f (x)，x∈(2T，3T)的反函数为
A．y=f -1(x)，x ∈ D B．y=f -1(x-2 T)，χ∈D
C．y=f -1(x+2T)，x∈D D．y=f -1(χ)+2T，χ∈ D
7．已知函数，f(x)：χ4+9x+5，则f(χ)的图象在(-1，3)内与x轴的交点的个数为
A．0个 B．1个 C．2个 D．3个
9．点(sinθ,cosθ)到直线χ·cosθ+y·sinθ+1=0的距离小于1/2 ，则θ的取值范围是
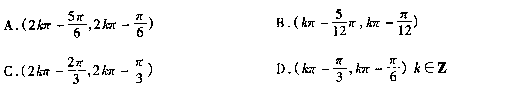
11．下列条件中，能确定三点A、B、P不共线的是
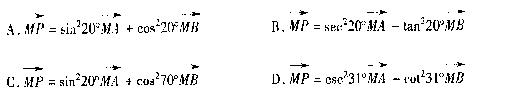
12．正四棱锥P-ABCD的所有棱长相等，E是PC中点，那么异面直线BE与PA所成的角的余弦
值等于
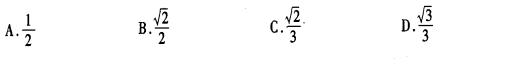
第Ⅱ卷 (非选择题共90分)
二、填空题(每小题4分。共4小题。共16分．)
16．已知．Χ4+y2=1，则下列结论正确的是
(请将你认为正确的结论的序号全部填入)．
①它的图象关于x轴对称；
②它的图象关于Y轴对称；
③它的图象关于原点对称；
④它的图象是一个封闭图形，且面积大于丌；
⑤它的图象是一个封闭图形，且面积小于丌．
三、解答题(共74分)
17．从4名男生和2名女生中任选3人参加演讲比赛．
(1)求所选3人中恰有1名女生的概率．
(2)求所选3人中至少有1名女生的概率．
(1)要得到y=f(χ)的图象，只需把y=g(x)的图象经过怎样的变换?
(2)求h(χ)=f(χ)-g(x)的最大值及对应的χ的值．
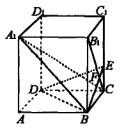
19．(12分)如图，已知正四棱柱ABCD—A1B1 C1D1中，底面边长AB=2，侧棱
BBl的长为4，过点B作BlC的垂线交侧棱CCl于点E，交B1 C于点F．
(1)求证：AlC上平面BED；
(2)求AlB与平面BDE所成的角的正弦值．
20．(12分)定义在R上的奇函数，f(χ)有最小正周期2，且x∈(0，1)时，f(χ)=
(1)求，f(χ)在[一1，1]上的解析式；
(2)判断．f(χ)在(O，1)上的单调性，并给予证明；
21．(12分)由原点0向三次曲线y=x3一3x2引切线，切于点P1(x1,,,y1)(0，Pl两点不重合)，再由
Pl引此曲线的切线，切于点P2(x2，y2)(Pl，P2不重合)．如此继续下去，得到点列{Pn(xn, yn)}．
(1)求xl；
(2)求xn与xn+l满足的关系式；
(3)求数列{xn}的通项公式．
高三年级质量检测
数学参考答案(文科)
一，选择题
A卷
| 题号 | l | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | lO | ll | 12 |
| 答案 | D | B | A | A | D | D | B | C | B | A | C | D |
B卷
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ll | 12 |
| 答案 | D | B | B | D | D | D | B | C | B | B | C | D |
提示：
