高考数学普通高等学校招生全国统一考试124
第I卷(本卷共10小题,每小题5分,共50分)
一. 选择题:在每小题列出的四个选项中,只有一项是符合题目要求的。
1. 已知集合![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
2. 设![]() 是等差数列,
是等差数列,![]() ,
,![]() ,则这个数列的前6项和等于( )
,则这个数列的前6项和等于( )
A. 12 B. 24 C. 36 D. 48
3. 设变量![]() 、
、![]() 满足约束条件
满足约束条件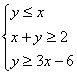 ,则目标函数
,则目标函数![]() 的最小值为( )
的最小值为( )
A. 2 B. 3 C. 4 D. 9
4. 设![]() ,
,![]() ,
,![]() ,则( )
,则( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5. 设![]() ,那么“
,那么“![]() ”是“
”是“![]() ”的( )
”的( )
A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件 D. 既不充分也不必要条件
6. 函数![]() (
(![]() )的反函数是( )
)的反函数是( )
A. ![]() (
(![]() ) B.
) B.
![]() (
(![]() )
)
C. ![]() (
(![]() ) D.
) D.
![]() (
(![]() )
)
7. 若![]() 为一条直线,
为一条直线,![]() 为三个互不重合的平面,给出下面三个命题:①
为三个互不重合的平面,给出下面三个命题:①
![]() ②
② ![]() ;③
;③ ![]() ,其中正确的命题有( )
,其中正确的命题有( )
A. 0个 B. 1个 C. 2个 D. 3个
8. 椭圆的中心为点E(![]() ),它的一个焦点为F(
),它的一个焦点为F(![]() ),相应于焦点F的准线方程为
),相应于焦点F的准线方程为![]() ,则这个椭圆的方程是( )
,则这个椭圆的方程是( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
9. 已知函数![]() (
(![]() 为常数,
为常数,![]() )的图象关于直线
)的图象关于直线![]() 对称,则函数
对称,则函数![]() 是( )
是( )
A. 偶函数且它的图象关于点(![]() )对称
B. 偶函数且它的图象关于点(
)对称
B. 偶函数且它的图象关于点(![]() )对称
)对称
C. 奇函数且它的图象关于点(![]() )对称
D. 奇函数且它的图象关于点(
)对称
D. 奇函数且它的图象关于点(![]() )对称
)对称
10. 如果函数![]() (
(![]() 且
且![]() )在区间
)在区间![]() 上是增函数,那么实数
上是增函数,那么实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
第II卷(本卷共12小题,共100分)
二. 填空题:本大题共6小题,每小题4分,共24分。把答案填在题中横线上。
11. ![]() 的二项展开式中
的二项展开式中![]() 的系数是 (用数字作答)
的系数是 (用数字作答)
12. 设向量![]() 与
与![]() 的夹角为
的夹角为![]() ,且
,且![]() =(3,3),
=(3,3),![]() ,则
,则![]() 。
。
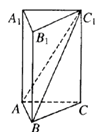 13. 如图,在正三棱柱
13. 如图,在正三棱柱![]() 中,AB=1。若二面角
中,AB=1。若二面角![]() 的
的
大小为![]() ,则点
,则点![]() 到直线AB的距离为
。
到直线AB的距离为
。
14. 若半径为1的圆分别与![]() 轴的正半轴和射线
轴的正半轴和射线![]() 相切,
相切,
则这个圆的方程为 。
15. 某公司一年购买某种货物400吨,每次都购买![]() 吨,运费为4万元/次,一年的
吨,运费为4万元/次,一年的
总存储费用为![]() 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则![]() = 吨。
= 吨。
16. 用数字0、1、2、3、4组成没有重复数字的五位数,则其中数字1、2相邻的偶数有 个(用数字作答)。
三. 解答题:本大题共6小题,共76分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
已知![]() ,
,![]() ,求
,求![]() 和
和![]() 的值。
的值。
18.(本小题满分12分)
甲、乙两台机床相互没有影响地生产某种产品,甲机床产品的正品率是0.9,乙机床产品的正品率是0.95。
(1)从甲机床生产的产品中任取3件,求其中恰有2件正品的概率(用数字作答);
(2)从甲、乙两台机床生产的产品中各任取1件,求其中至少有1件正品的概率(用数字作答)
19.(本小题满分12分)
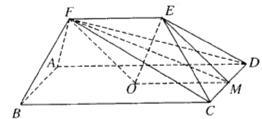 如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱![]() 。
。
(1)证明FO//平面CDE;
(2)设![]() ,证明EO⊥平面CDF。
,证明EO⊥平面CDF。
20.(本小题满分12分)
已知函数![]() ,其中
,其中![]() ,
,![]() 为参数,且
为参数,且![]() 。
。
(1)当![]() 时,判断函数
时,判断函数![]() 是否有极值;
是否有极值;
(2)要使函数![]() 的极小值大于零,求参数
的极小值大于零,求参数![]() 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数![]() ,函数
,函数![]() 在区间(
在区间(![]() )内都是增函数,求实数
)内都是增函数,求实数![]() 的取值范围。
的取值范围。
21.(本小题满分14分)
已知数列![]() 满足
满足![]() ,并且
,并且![]() (
(![]() 为非零参数,
为非零参数,![]() 2,3,4,……)
2,3,4,……)
(1)若![]() 成等比数列,求参数
成等比数列,求参数![]() 的值;
的值;
(2)设![]() ,常数
,常数![]() 且
且![]() ,证明
,证明![]() (
(![]() )
)
22.(本小题满分14分)
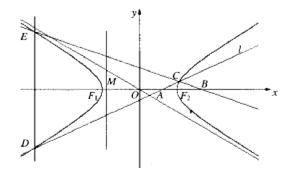 如图,双曲线
如图,双曲线![]() (
(![]() )的离心率为
)的离心率为![]() ,
,![]() 分别为左、右焦点,M为左准线与渐近线在第二象限内的交点,且
分别为左、右焦点,M为左准线与渐近线在第二象限内的交点,且![]() 。
。
(1)求双曲线的方程;
(2)设A(![]() )和B(
)和B(![]() )(
)(![]() )是
)是![]() 轴上的两点,
轴上的两点,
过点A作斜率不为0的直线![]() ,使得
,使得![]() 交双曲线于C、D两点,
交双曲线于C、D两点,
作直线BC交双曲线于另一点E,证明直线DE垂直于![]() 轴。
轴。
普通高等学校招生全国统一考试
参考答案
一. 选择题:1. A 2. B 3. B 4. A 5. C 6. D 7. C 8. D 9. D 10. B
二. 填空题:11. 35 12. ![]() 13.
13. ![]() 14.
14. ![]() 15. 20 16. 24
15. 20 16. 24
三. 解答题
17.解法一:由![]() ,得
,得![]() ,则
,则![]() ,
,![]()
因为![]()
![]() ,所以
,所以![]() ,
,![]()
![]()
![]()
解法二:由![]() ,得
,得![]()
解得![]() 或
或![]() 。由已知
。由已知![]() ,故舍去
,故舍去![]() ,得
,得![]()
因此,![]() ,
,![]() ,那么
,那么![]()
且![]() ,故
,故![]()
![]()
18.(1)解:任取甲机床的3件产品中恰有2件正品的概率为![]()
(2)解法一:记“任取甲机床的1件产品是正品”为事件A,“任取乙机床的1件产品是正品”为事件B。则任取甲、乙两台机床的产品各1件,其中至少有1件正品的概率为
![]()
解法二: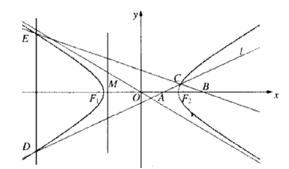 运用对立事件的概率公式,所求的概率为
运用对立事件的概率公式,所求的概率为![]()
19. (1)证明:取CD中点M,连结OM,在矩形ABCD中
![]() ,又
,又![]() ,则
,则![]() 。连结EM,
。连结EM,
于是四边形EFOM为平行四边形
∴ FO//EM
又
∵ FO![]() 平面CDE,且EM
平面CDE,且EM![]() 平面CDE,∴ FO//平面CDE
平面CDE,∴ FO//平面CDE
(2)证明:连结FM,由(1)和已知条件,在等边![]() 中,CM=DM,EM⊥CD且
中,CM=DM,EM⊥CD且![]() 。因此平行四边形EFOM为菱形,从而EO⊥FM
。因此平行四边形EFOM为菱形,从而EO⊥FM
∵ CD⊥OM,CD⊥EM ∴ CD⊥平面EOM,从而CD⊥EO
而FM![]() CD=M,所以
CD=M,所以![]() 平面CDF
平面CDF
20. (1)解:当![]() 时,
时,![]() ,则函数
,则函数![]() 在(
在(![]() )上是增函数,故无极值。
)上是增函数,故无极值。
(2)解:![]() ,令
,令![]() ,得
,得![]()
由![]() 及(1),只考虑
及(1),只考虑![]() 的情况
的情况
当![]() 变化时,
变化时,![]() 的符号及
的符号及![]() 的变化情况如下表:
的变化情况如下表:
|
|
| 0 |
|
|
|
|
| + | 0 | - | 0 | + |
|
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
因此,函数![]() 在
在![]() 处取得极小值
处取得极小值![]() ,且
,且![]()
要使![]() ,必有
,必有![]() ,可得
,可得![]() ,所以
,所以![]()
(3)解:由(2)知,函数![]() 在区间
在区间![]() 与
与![]() 内都是增函数
内都是增函数
由题设,函数![]() 在
在![]() 内是增函数,则
内是增函数,则![]() 须满足不等式组
须满足不等式组![]() 或
或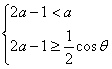
由(2),参数![]() 时,
时,![]() ,要使不等式
,要使不等式![]() 关于参数
关于参数![]() 恒成立,必有
恒成立,必有![]()
综上,解得![]() 或
或![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]()
21.(1)解:由已知![]() ,且
,且![]() ,
,![]()
![]() 若
若![]() 成等比数列,则
成等比数列,则![]() ,即
,即![]() ,而
,而![]() ,解得
,解得![]()
(2)证明:设![]() ,由已知,数列
,由已知,数列![]() 是以
是以![]() 为首项、
为首项、![]() 为公比的等比数列,故
为公比的等比数列,故![]() ,则
,则![]()
![]()
因此,对任意![]() ,
, ![]()
![]()
![]()
![]()
当![]() 且
且![]() 时,
时,![]() ,
,![]() ,所以
,所以

![]() (
(![]() )
)
22. (1)解:根据题设条件,![]() ,
,![]() ,
,
设点M(![]() ),则
),则![]() 满足
满足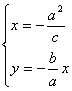
因![]() ,解得
,解得![]() ,
,
故![]()
![]()
利用![]() ,得
,得![]() ,于是
,于是![]() ,
,![]() ,因此,所求双曲线方程为
,因此,所求双曲线方程为![]()
(2)解:设C(![]() ),D(
),D(![]() ),E(
),E(![]() ),则直线
),则直线![]() 的方程为
的方程为
![]() 于是C
于是C![]() 、D
、D![]() 两点坐标满足
两点坐标满足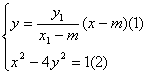
将(1)代入(2)得
由![]()

由已知,显然![]() 。于是
。于是![]() 。因为
。因为![]() ,得
,得![]()
同理,C(![]() )、E(
)、E(![]() )两点坐标满足
)两点坐标满足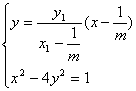
可解得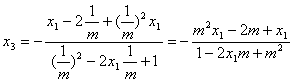
所以![]() ,故直线DE垂直于
,故直线DE垂直于![]() 轴
轴