高考数学普通高等学校招生全国统一考试126
数学试题(文科)
第Ⅰ卷(共 50分)
一、选择题:本大题共 10小题,每小题 5分,共 50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)设集合 A=x|-1≤x≤2,B=x0≤x≤4,则 A∩B=
(A).[0,2] (B).[1,2] (C).[0,4] (D).[1,4]
(2)在二项式![]() 的展开式中,含
的展开式中,含![]() 的项的系数是
的项的系数是
(A).15 (B).20 (C).30 (D).40
(3)抛物线![]() 的准线方程是
的准线方程是
(A)x=-2 (B)x=-4 (C)y=-2 (D)y=-4
(4)已知![]() 则
则
(A)n<m<1 (B)m<n<1
(C)1<m<n (D)1<n<m
(5)设向量 a,b,c满足 a+b+c=0,且 a⊥b,a=1,b=2,则c 2 =
(A)1 (B)2 (C)4 (D)5
(6)函数 f(x)=![]() 在区间[-1,1]上的最大值是
在区间[-1,1]上的最大值是
(A)-2 (B)0 (C)2 (D)4
(7)“a>0,b>0”是“ab>0”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
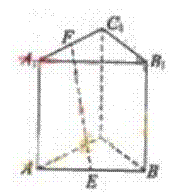 (8)如图,正三棱柱
(8)如图,正三棱柱 ![]() 的各棱长都为 2,
的各棱长都为 2,![]() 分别为
分别为
(A)2 (B)![]() (C)
(C)![]() (D)
(D)![]()
(9)在平面直角坐标系中,不等式组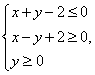 表示的平面区域的面积是
表示的平面区域的面积是
(A)![]() (B)4 (C)
(B)4 (C)![]() (D)2
(D)2
(10)对![]() ,记
,记![]() 函数
函数![]() 的最小值是
的最小值是
(A)0 (B)![]() (C)
(C)![]() (D)3
(D)3
第Ⅱ卷(共 100分)
二、填空题:本大题共 4小题,每小题 4分,共 16分。
(11)不等式
![]() 的解集是
的解集是![]() .
.
(12)函数![]() 的值域是
的值域是![]()
(13)双曲线![]() 上的点到左焦点的距离与到左准线的距离的比是3,则m 等于
上的点到左焦点的距离与到左准线的距离的比是3,则m 等于
![]() 。
。
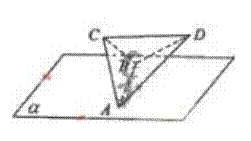 (14)如图,正四面体 ABCD的棱长为 1,平面α过棱 AB, 且 CD∥α,则正四面体上的所有点在平面α内的射
(14)如图,正四面体 ABCD的棱长为 1,平面α过棱 AB, 且 CD∥α,则正四面体上的所有点在平面α内的射
影构成的图形面积是![]() 。
。
三、解答题:本大题共 6小题,每小题 14分,共 84分。解答应写出文字说明,证明过程或演算步骤。
(15)若![]() 是公差不为 0的等差数列
是公差不为 0的等差数列![]() 的前
的前![]() 项和,且
项和,且![]() 成等比数列
成等比数列
(Ⅰ)求数列![]() 的公比;
的公比;
(Ⅱ)![]() =4,求
=4,求![]() 的通项公式。
的通项公式。
(16)如图,函数![]() 其中(
其中(![]() )的图象与
)的图象与![]() 轴交于点(0,1)
轴交于点(0,1)
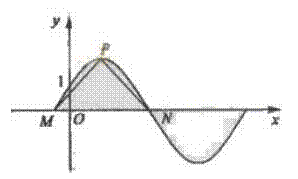 (Ⅰ)求
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)设![]() 是图象上的最高点,M,N是图象与
是图象上的最高点,M,N是图象与![]() 轴的交点,求
轴的交点,求![]() 与
与![]() 的夹角。
的夹角。
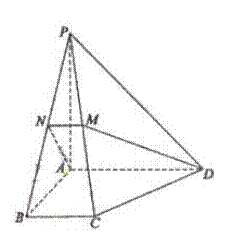 (17)如图,在四棱锥 P—ABCD中,底面为直角梯形, AD∥BC,∠BAD=90°,PA⊥底面 ABCD,
(17)如图,在四棱锥 P—ABCD中,底面为直角梯形, AD∥BC,∠BAD=90°,PA⊥底面 ABCD,
且 PA=AD=AB=2BC,M、N分别为 PC、PB的中点。
(Ⅰ)求证:PB⊥DM;
(Ⅱ)求 BD与平面 ADMN所成的角。
(18)甲、乙两袋装有大小相同的红球和白球,甲袋装有2个红球,2个白球;乙袋装有 2个红球,n个白球,现从甲、乙两袋中任取 2个球。
(Ⅰ)若![]() ,求取到的4个球全是红球的概率;
,求取到的4个球全是红球的概率;
(Ⅱ)若取到的4个球中至少有 2个红球的概率为 ![]() ,求 n。
,求 n。
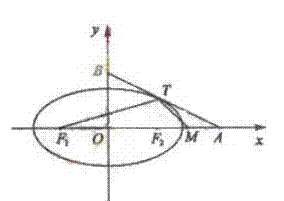 (19)如图,椭圆
(19)如图,椭圆![]() 与过
与过![]() ,
,![]() 的直线有且只有一个公共点
的直线有且只有一个公共点![]() ,且椭圆的离心率
,且椭圆的离心率![]() ,
,
(Ⅰ)求椭圆的方程
(Ⅱ)设![]() 分别为椭圆的左、右焦点,求证
分别为椭圆的左、右焦点,求证![]()
(20)设![]() ,若 a+b+c=0,
,若 a+b+c=0,![]() ,求证
,求证
(Ⅰ)方程![]() 有实根;
有实根;
(Ⅱ)![]()
(Ⅲ)设![]() 是方程
是方程![]() 的两个实根,则
的两个实根,则![]()
数学试题(文科)参考答案
一、选择题:本题考察基本知识和基本运算。每小题 5分,共 50分。
(1)A(2)B (3)A (4)D (5)D (6)C (7)A (8)C (9)B (10)C
二、填空题:本题考察基本知识和基本运算。每小题 4分,满分 16分。
(11)![]() (12)
(12)![]() (13)
(13)![]() (14)
(14)![]()
三、解答题
(15)本题主要考察等差、等比数列的基本知识、考查运算及推理
能力。满分 14分。
解:(Ⅰ)设数列![]() 的公差为
的公差为![]() ,由题意,得
,由题意,得 ![]()
所以![]()
因为![]()
所以 ![]()
故公比![]()
(Ⅱ)因为![]()
所以![]()
因此![]()
(16)本题主要考查三角函数的图象,已知三角函数值求角,向量夹角的计算等基础知识和基本的运算能力。满分14分。
解:(Ⅰ)因为函数图象过点(0,1)
所以 ![]() ,即
,即 ![]()
因为![]() 所以
所以![]() .
.
(Ⅱ)由函数![]() 及其图象,得
及其图象,得
![]()
所以 ![]() 从而
从而
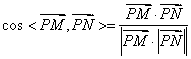
![]()
故![]() .
.
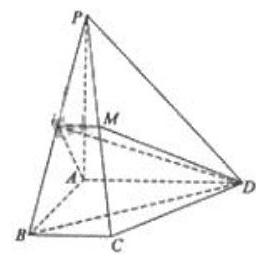 17.本题主要考查空间线线、线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力。满分14分。
17.本题主要考查空间线线、线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力。满分14分。
解:方法一:
(Ⅰ)因为N是PB的中点,PA=AB,
所以AN⊥PB.
因为AD⊥面PAB, 所以AD⊥PB.
从而PB⊥平面ADMN.
![]()
所以PB⊥DM.
(Ⅱ)连结DN,
因为PB⊥平面ADMN,
所以∠BDN是BD与平面ADMN所成的角.
在![]() 中,
中, ![]()
故BD与平面ADMN所成的角是![]() .
.
方法二:
如图,以A为坐标原点建立空间直角坐标系![]() ,设BC=1,则
,设BC=1,则![]()
![]()
(Ⅰ)因为![]()
![]() ,
,
所以PB⊥DM .
(Ⅱ)因为 ![]()
![]() ,
,
所以PB⊥AD. 又PB⊥DM.
因此![]() 的余角即是BD与平面ADMN所成的角.
的余角即是BD与平面ADMN所成的角.
因为 ![]() ,所以
,所以![]() =
=![]()
因此BD与平面ADMN所成的角为![]() .
.
(18)本题主要考查排列组合、概率等基本知识,同时考查逻辑思维能力和数学应用能力。满分14分。
解:(Ⅰ)记“取到的4个球全是红球”为事件A.
![]()
(Ⅱ)记“取到的4个球至多有一个红球”为事件B,“取到的4个球只有1个红球”为事件![]() ,“取到的4个球全是白球”为事件
,“取到的4个球全是白球”为事件![]() .
.
由题意,得
![]()
![]()
![]()
![]()
![]()
所以 ![]()
![]()
![]() .
.
化简,得 ![]() 解得
解得![]() ,或
,或![]() (舍去),
(舍去),
故 ![]() .
.
(19)本题主要考查直线与椭圆的位置关系、椭圆的几何性质,考查解析几何的基本思想方法和综
合解题能力。满分 14分。
解:(Ⅰ)过 A、B的直线方程为
![]()
因为由题意得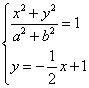 有惟一解。
有惟一解。
即![]() 有惟一解,
有惟一解,
所以![]() ,
,
故![]()
又因为 ![]() ,即
,即![]() ,
,
所以![]()
从而得![]()
故所求的椭圆方程为![]() .
.
(Ⅱ)由(Ⅰ)得![]() ,所以
,所以 ![]()
由 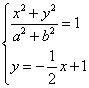 解得
解得 ![]() 因此
因此![]() .
.
从而 ![]() ,
,
因为![]() ,
,
所以![]()
(20)本题主要考查二次函数的基本性质、不等式的基本性质与解法,以及综合运用所学知识分析和解决问题的能力。满分 14分。
证明:(Ⅰ)若 a = 0, 则 b = -c ,
f (0) f (1) = c (3a + 2b + c )
![]() ,
,
与已知矛盾,
所以 a ≠ 0.
方程![]() = 0 的判别式
= 0 的判别式
![]()
由条件 a + b + c
= 0,消去 b,得
![]()
![]()
故方程 f (x) = 0 有实根.
(Ⅱ)由条件,知
![]() ,
, ![]() ,
,
所以![]()
![]()
因为 ![]()
所以 ![]()
故 ![]()