高三数学三基小测试卷数列
班级 姓名 座号 评分
一、选择题:(本大题共6小题,每小题6分,共3 6分.在每小题给出的四个选项中,只有一项是符合题目要求的,将正确答案填入题中括号中.)
1.等差数列{bn}中,b1=1, b1+b2+b3+……+b10=145, 则数列{bn}的通项公式bn是 ( )
(A)3n-2 (B)4-3n (C)16n-15 (D)![]()
2.在公比为q且各项均为正数的等比数列{an}中,若an-3·an+1=ak2(n, k均为自然数),则ak为 ( )
(A)a1qn-1 (B)a1qn-2 (C)a1qn-3 (D)以上答案都不正确
3.在等差数列{an}中,a3+a7-a10=8, a11-a4=4, 记Sn=a1+a2+a3+……+an,则S13等于 ( )
(A)168 (B)156 (C)78 (D)152
4.等差数列{an}的前n项和是Sn,a3+a8>0, S9<0, 则S1, S2, S3, ……,Sn中最小的是 ( )
(A)S9 (B)S8 (C)S5 (D)S4
5.已知等比数列{an}的前n项和是Sn,若S30=13S10, S10+S30=140,则S20的值是 ( )
(A)90 (B)70 (C)50 (D)40
6.等比数列{an}中,公比q=![]() ,且a3+a6+a9+……+a99=60,那么a1+a2+a3+……+a99的值等于
( )
,且a3+a6+a9+……+a99=60,那么a1+a2+a3+……+a99的值等于
( )
(A)300 (B)420 (C)90 (D)100
二、填空题:(本大题共5小题,每小题6分,共30分。把答案填在题中横线上。)
7.在等比数列{an}中,记Sn=a1+a2+a3+……+an,已知a5=2S4+3,
a6=2S5+3,则此数列的公比q的值是 .
8.等差数列{an}的首项a1=-5,它的前11项的平均值是5,若从中抽去一项,余下的10项的平均值是4.6,则抽去的这一项是第 项.
9.已知x=11,则![]() = .
= .
10.某产品,计划每年成本降低q%,若三年后的成本是a元,则现在的成本是 元.
11.数列{an}中,若a1=5, an=Sn-1 (n≥2),则an = .
三、解答题:(本大题共2小题,共34分,解答应写出文字说明,或演算步骤)
12、(本小题满分14分)已知三数成等比数列,若把第二个数增加4,则三数成等差数列,若再把第三个数增加32,则它们又成了等比数列,求这三个数。
13 、(本小题满分20分)已知f (x)=a1x+a2x2+a3x3+……+anxn,且a1, a2, a3,……,an组成等差数列(n为正偶数),又f (1)=n2 , f (-1)=n ,
(1) 求数列的通项公式an; (2) 试比较f (![]() )与3的大小,并说明理由.
)与3的大小,并说明理由.
高三年40分钟三基小测数学试卷——数列参考答案
一、选择题:A B B C D B
二、填空题: ⑺、3;
⑻、8;
⑼、![]() ; ⑽、
; ⑽、 ![]() ;
;
⑾、a1=5, an=5·2n-2 (n≥2).
三、解答题:
12. 解:设三数为a、b、c,依题意有
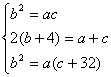 ……………… 7分
……………… 7分
解得a、b、c三个数为2, 6, 18或![]() , -
, -![]() ,
, ![]() .……………… 14分
.……………… 14分
13.解:(1) 设数列{an}的公差为d, f (1)=a1+a2+a3+……+an=![]() =n2,
=n2,
∴ a1+an=2n, 又∵ f (-1)= -a1+a2-a3+……-an-1+an=n, ∴![]() nd=n,
nd=n,
∴ d=2, 则a1=1, an=2n-1, ……………… 10分
(2) f (![]() )=
)=![]() +3(
+3(![]() )2+5(
)2+5(![]() )3+……+(2n-1) (
)3+……+(2n-1) (![]() )n
…………………………①
)n
…………………………①
①×![]() 得
得![]() f (
f (![]() )=(
)=(![]() )2+3(
)2+3(![]() )3+5(
)3+5(![]() )4+……+(2n-1) (
)4+……+(2n-1) (![]() )n+1 ……………②
)n+1 ……………②
①-②得![]() f (
f (![]() )=
)=![]() +2[(
+2[(![]() )2+(
)2+(![]() )3+……+(
)3+……+(![]() )n]-(2n-1)(
)n]-(2n-1)(![]() )n+1, … 16分
)n+1, … 16分
∴f (![]() )=1+4·
)=1+4·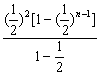 -(2n-1)(
-(2n-1)(![]() )n+1
)n+1
=3-![]() -(2n-1)(
-(2n-1)(![]() )n+1<3.
……………… 20分
)n+1<3.
……………… 20分