高三数学统一检测试卷
(文)
本试卷分为第I卷(选择题)和第II卷(非选择题)两部分,共150分,
考试时间120分钟。
第I卷(非选择题 共60分)
注意事项: 1、考生务必将自己的姓名、考号写在规定的位置。考试结束,可只交回第II卷。
2、答第I卷时,考生把答案选出后,务必将答案写到第II卷规定位置,否则不予给分。
一、选择题:本大题共12小题,每小题5分,共60分。在每小题列出的四个选项中,只有一项是符合题目要求的。
1、若不等式![]() 的解集相同,则
的解集相同,则![]() 等于 (
)
等于 (
)
A.12 : 7 B.7 : 12 C.(-12 : 7) D.(-3): 4
2、设集合M={-1,1,0},N={1,2,3,4,5}, ,映射f:M→N,使对任意的x∈M,都有x+f(x)是奇数,这样的映射f的个数为
A.10 B.11 C.12 D.13
3、将函数y=![]() (
(![]() )(
)(![]() R)的图象上所有的点向左平行移动
R)的图象上所有的点向左平行移动![]() 个单位长度,再把图像上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图象的解析式为
个单位长度,再把图像上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图象的解析式为
A.![]() (
(![]() )(
)(![]() R) B.
R) B.![]() (
(![]() )(
)(![]() R)
R)
C.![]() (
(![]() )(
)(![]() R) D.
R) D.![]() (
(![]() )(
)(![]() R
R
4 已知![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
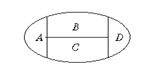 5、用6种不同的颜色把下图中A、B、C、D四块区域分开,允许同一色涂不同的区域,但相邻的区域不能涂同一色,则不同的涂法共有
5、用6种不同的颜色把下图中A、B、C、D四块区域分开,允许同一色涂不同的区域,但相邻的区域不能涂同一色,则不同的涂法共有
A.400种 B.460种
C.480种 D.496种
6 .设![]() ,
,![]() ,则满足条件
,则满足条件![]() ,
,![]() 的动点P的变化范围(图中阴影部分含边界)是
的动点P的变化范围(图中阴影部分含边界)是
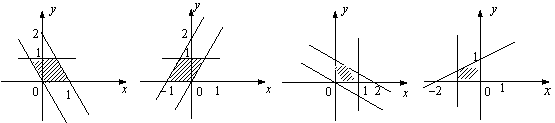 |
A. B. C. D.
7已知![]() ,
,![]() 为互相垂直的单位向量,
为互相垂直的单位向量,![]() 且
且![]() 与
与![]() 的夹角为锐角,则实数
的夹角为锐角,则实数![]() 的取值范围是
的取值范围是
A.(-∞,2)∪(-2,![]() )
B.(
)
B.(![]() ,+∞)
,+∞)
C.(-2,![]() )∪(
)∪(![]() ,+∞)
D.(-∞,
,+∞)
D.(-∞,![]() )
)
8、若A∩B=![]() ,且A∪B={a,b},则满足条件的集合A、B的组数有
,且A∪B={a,b},则满足条件的集合A、B的组数有
A.2 B.4 C.6 D.8
9、甲、乙、丙投篮一次命中的概率分别为![]() 、
、![]() 、
、![]() ,现三人各投篮一次至少有1人命中的概率为
,现三人各投篮一次至少有1人命中的概率为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知![]() 展开式中常数项为1120,其中实数
展开式中常数项为1120,其中实数![]() 是常数,则展开式中各项系数的和为
是常数,则展开式中各项系数的和为
A.![]() B.
B.![]() C.1或
C.1或![]() D.1或
D.1或![]()
11已知k是常数,若双曲线![]() =1的焦距与k的取值无关,则k的取值范围是
=1的焦距与k的取值无关,则k的取值范围是
A.-2<k≤2 B.k>5 C.-2<k≤0 D.0≤k<2
12正三棱锥的侧面与底面所成的二面角的余弦值为![]() ,则其相邻两侧面所成的二面角的余弦值是
,则其相邻两侧面所成的二面角的余弦值是
A.![]() B.
B.![]() C.
C.![]() D.0
D.0
统一检测试卷
 高三数学(文)
高三数学(文)
第II卷(非选择题,共90分)
| 题号 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
| 得分 |
|
|
|
|
|
|
|
|
第I卷答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 总分 |
| 答案 |
二、填空题:本大题共4小题,每小题4分,共16分,把答案写在横线上。
13.若曲线![]() 在点
在点![]() 处切线平行于直线
处切线平行于直线![]() ,则点
,则点![]() 的坐标为________.
的坐标为________.
14.已知│![]() │=3,│
│=3,│![]() │=5,且
│=5,且![]() =-12,则
=-12,则![]() 在
在![]() 的方向上的投影为__________
的方向上的投影为__________
15.已知S是△ABC所在平面外一点, D是SC的中点,若![]() , 则
, 则![]()
16.对于实数x、y,定义新运算x*y=ax+by+1,其中以a、b是常数,等式右边是通常的加法和乘法运算,若3*5=15,4*7=28,则1*1=_______.
三、解答题(本大题共6小题,共74分)
17.(本小题满分12分)在![]() 中,a、b、c分别为角A、B、C的对边,若
中,a、b、c分别为角A、B、C的对边,若![]() =(
=(![]() ,1),
,1),![]() =(
=(![]() ,4),且
,4),且![]() .
.
(Ⅰ)求角A的度数;
(Ⅱ)当a=![]() ,
,![]() 时,求边长b和角B的大小.、
时,求边长b和角B的大小.、
18.(本小题满分12分)某厂生产的A产品按每盒10件进行包装,每盒产品均需检验合格后方可出厂.质检办法规定:从每盒10件A产品中任抽4件进行检验,若次品数不超过1件,就认为该盒产品合格;否则,就认为该盒产品不合格.已知某盒A产品中有2件次品.
(Ⅰ)求该盒产品被检验合格的概率;
(Ⅱ)若对该盒产品分别进行两次检验,求两次检验得出的结果不一致的概率.
19、(本小题满分12分)如图,已知三棱锥P—ABC中,PA⊥平面ABC,PA=3,AC=4,PB=PC=BC.
(1)求三棱锥P—ABC的体积V;
(2)作出点A到平面PBC的垂线段AE,并求AE的长;
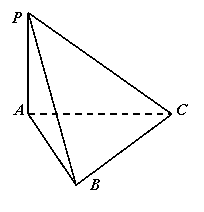 (3)求二面角A—PC—B的大小.
(3)求二面角A—PC—B的大小.
20、(本小题满分12分)数列{![]() }的前
}的前![]() 项和
项和![]() 满足:
满足:![]() .
.
 (1)求数列{
(1)求数列{![]() }的通项公式
}的通项公式![]() ;
;
(2)数列{![]() }中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由
}中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由
21. (本小题满分13分) 已知实数![]() 有极大值32.
有极大值32.
(1)求函数![]() 的单调区间;(2)求实数
的单调区间;(2)求实数![]() 的值.
的值.
22. (本小题满分13分)已知双曲线C的中心在原点,抛物线![]() 的焦点是双曲线C的一个焦点,且双曲线过点(1,
的焦点是双曲线C的一个焦点,且双曲线过点(1,![]() ),且直线
),且直线![]() :
:![]() 与双曲线C交于A、B两点,(I)求双曲线的方程;(II)
与双曲线C交于A、B两点,(I)求双曲线的方程;(II)![]() 为何值时
为何值时![]()
统一检测试卷 数学(文科)答案
一选择题本大题共12小题,每小题5分,共60分。
1 A 2 C 3. B 4 B 5 C 6. B 7 A 8 B 9. C 10. C 11 C12 D
二.填空题 (本大题共4小题,每小题4分,共16分)
13.![]() 14.
14. ![]() 15.
15. ![]() 16.
16. ![]()
三.解答题
17 解:(Ⅰ)∵![]() ∥
∥![]() ∴
∴![]() ………………………………….…2分
………………………………….…2分
∴2[1-cos(B+C)]-(2cos2A-1)-![]() =0
=0
∵cos(B+C)=-cosA,∴4cos2A-4cosA+1=0,………………………………….…….5分
∴(2cosA-1)2=0,即cosA=![]()
又∵00<A<1800 , ∴A=60° ………………………………………………………….6分
(Ⅱ)∵S△ABC=![]() bc×sinA, ∴
bc×sinA, ∴![]() bc×
bc×![]() =
=![]() ,即bc=2……①…………………………….7分
,即bc=2……①…………………………….7分
∴a2=b2+c2-2bccosA=b2+c2-bc=(b+c)2-3bc=3,
∴(b+c)2=9 即 b+c=3……②………………………………………………………….9分
由①②解得
![]() 或
或![]() . ………………………………………………………………………….10分
. ………………………………………………………………………….10分
当b=2时sinB=![]() =1,B=90°
=1,B=90°
当b=1时sinB=![]() =
=![]() ,∵b<a,B<A, ∴B=30°…………………………………….12分
,∵b<a,B<A, ∴B=30°…………………………………….12分
18.解: (Ⅰ)从该盒10件产品中任抽4件,有等可能的结果数为![]() 种,……………1分
种,……………1分
其中次品数不超过1件有![]() 种, ………………………2分
种, ………………………2分
被检验认为是合格的概率为![]()
![]() . …………………………………6分
. …………………………………6分
(Ⅱ)两次检验是相互独立的,可视为独立重复试验,……………………………………7分
因两次检验得出该盒产品合格的概率均为![]() ,
,
故“两次检验得出的结果不一致”即两次检验中恰有一次是合格的概率为
![]()
![]() .……………………………………………………………………11分
.……………………………………………………………………11分
答:该产品被认为是合格的概率为![]() ;两次检验结果不一致的概率为
;两次检验结果不一致的概率为![]() .………12
.………12
19.解:(1)∵PA⊥平面ABC,PB=PC,由射影定理得,AB=AC=4.
∵PA⊥平面ABC,∴PA⊥AC.
在Rt△PAC中,可求出PC=5,则PB=BC=5.
取BC中点D,连AD.在等腰△ABC中,求出底边上的高AD=![]() .
.
 ∴V=
∴V=![]() ·
·![]() ·5·
·5·![]() ·3=
·3=![]() . 4分
. 4分
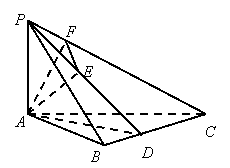
(2)连PD,则PD⊥BC,又AD⊥BC,
∴BC⊥平面PAD.又BC![]() 平面PBC,
平面PBC,
∴平面PAD⊥平面PBC.
作AE⊥PD于E,则AE⊥平面PBC,
AE为点A到平面PBC的垂线段.
在Rt △PAD中,由PA·AD=AE·PD,
即3·![]() =AE·
=AE·![]() ,求出AE=
,求出AE=![]() .8分
.8分
(3)作AF⊥PC于F,连EF,由三垂线逆定理,得EF⊥PC.
∠AFE为二面角A—PC—B的平面角.
在Rt△PAC中,由PA·AC=PC·AF,即3·4=5·AF,求出AF=![]() ,
,
∴sinAFE=![]() =
=![]() ·
·![]() =
=![]() . 12分
. 12分
即二面角A—PC—B为arcsin![]()
.20. 解 (1)当![]() 时有:
时有:![]()
两式相减得:![]() ,…………………………2’
,…………………………2’
∴![]() ,又
,又![]() ,∴
,∴ ![]() .
.
∴数列{![]() }是首项6,公比为2的等比数列.
}是首项6,公比为2的等比数列.
从而![]() ,∴
,∴![]() .………………………………………………6’
.………………………………………………6’
(2)假设数列{![]() }中存在三项
}中存在三项![]() ,它们可以构成等差数列,
,它们可以构成等差数列,
![]() 只能是
只能是![]() ,………………………………………………8’
,………………………………………………8’
![]() ,
,
即![]() .∴
.∴![]() ……………………………………………10’
……………………………………………10’
![]() 、
、![]() 、
、![]() 均为正整数,
均为正整数,
∴(*)式左边为奇数右边为偶数,不可能成立.
因此数列{![]() }中不存在可以构成等差数列的三项.……………………
}中不存在可以构成等差数列的三项.……………………
21.解: (1)![]()
![]() ………………………………………………3分
………………………………………………3分
令![]()
![]() ………………………………………4分
………………………………………4分
![]() ………………………………………………………5分
………………………………………………………5分
![]() ……………7分
……………7分
∴函数![]() 的单调递增区间为
的单调递增区间为![]() ……7分
……7分
∴函数![]() 的单调递减区间为
的单调递减区间为![]() ………………………………8分
………………………………8分
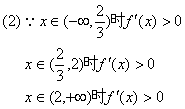
![]() 时,取得极大值……………………………………10分
时,取得极大值……………………………………10分
即 ![]()
解得 a=27………………………………………………………………13分
22解:(I)由题意设双曲线方程为![]() ,
,
把(1,![]() )代入得
)代入得![]() ①
……1分
①
……1分
又![]() 的焦点是(
的焦点是(![]() ,0),
,0),
故双曲线的![]() ……2分
……2分
与①联立,消去![]() 可得
可得
![]() ,
,![]()
∴ ![]() ,
,![]() (不合题意舍去)
(不合题意舍去)
于是![]() ,∴ 双曲线方程为
,∴ 双曲线方程为![]() ……5分
……5分
(II)由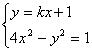 消去
消去![]() 得
得![]() ②
②
当![]() ,即
,即![]() (
(![]() )时,
)时,
![]() 与C有两个交点A、B
……8分
与C有两个交点A、B
……8分
设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),
),
因![]() ,故
,故![]() ,即
,即![]() ,
……10分
,
……10分
由②知![]() ,
,![]() ,
,
代入可得![]()
化简得![]() ,∴
,∴ ![]() ,
,
检验符合条件,故当![]() 时,
时,![]() ……13分
……13分