高三数学小题训练3
班级 学号 姓名 得分
一、选择题（共10题，每题只有一个正确答案，每题7分，共70分）
1．试在下列四个命题中找出一个与命题“无火不冒烟”等价的命题（ ）
A．若有火必冒烟 B．虽无火但有可能冒烟
C．冒烟处必有火 D．虽无烟但可能有火
2． 已知事件A、B是相互独立事件，则下列各对事件不是相互独立事件的是（ ）
A． A与
B．
与B C．A与
D．与
3．
函数
，则
的最大值为 （ ）
A． 
B．
C．
D．
4． 在
的展开式中，含
的项的系数是以
为通项公式的数列
的 （ ）
A．第24项 B．第20项 C．第11项 D．第3项
5．关于x的不等式
的解是
或
，则实数a的值为
A．
B．－2
C．
D．2
6． 在半径为R的球内，有一个内接正三棱锥，它的底面上的三个顶点恰好在同一个大圆上，一个动点从三棱锥的一个顶点出发沿球面运动，经过其余三顶点后返回，则经过的最短路程是 （ ）
A．
B．
C．
D．
7．函数
的值域是 （ ）
A．[－1，1] B．[
]
C．[
] D．[
]
8．已知平面上的直线
的方向向量
，点
和点
在直线上的射影分别为
，且
，其中
（ ）
A．
B．
C． 
D．
9． 不等式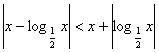
的解集为 （ ）
A．（0，1） B．
C．
D．
10． 正三角形ABC的顶点A为双曲线
的右顶点，顶点B，C在双曲线的右支上，则
的取值范围是 （ ）
A．
YCY B．
C．
D．
二、填空题（共6 题，请将答案写在横线上，每题 5分，共 30 分）
11． 如果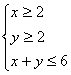
，则目标函数
的最大值为
.
12． 口袋里有4个白球和n个红球，从中随机摸出两个球，这两个球颜色相同的概率大于
，则n的最小值为
.
13．在棱长为1的正方体
中，过对角线
作截面
，则截面
面积的最小值等于
.
14． 设有两个命题：
①不等式
的解集是R；②函数
是减函数.
若这两个命题有且仅有一个是正确的，则实数
的范围是 .
15．在实数集R上定义运算∽：x∽y=x(1-y.),若(x-a)∽(x+a)<1对任意实数x都成立，则实数a的取值范围是 。
16．如图，在ΔABC中BC=2，AB+AC=3，中线AD的长为y，若AB的长为x，则y与x函数关系式为
。
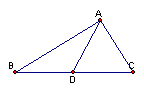
第16题图
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
11、 . 12. 13、 .
14. 15、 . 16.
附加题：（06上海模拟）设函数
在
上满足
, 
且在闭区间[0, 7]上只有
.
⑴试判断函数
的奇偶性;
⑵试求方程
在闭区间
上的根的个数, 并证明你的结论.
1．C 2．C 3．B 4．B 5．B
6．B 7．C 8．D 9．A 10．D
11．14 12．13
1 3．
14．
15．
提示：由定义有
(x-a)∽(x+a)<1
对
都成立，由
即得。
16．
；提示：
，两式相加整理得
，其中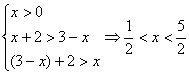
。
附加：解⑴由
∵在
上只有
∴
∴
故为非奇非偶函数。
………6′
⑵由
得 
∴是以10为周期的函数. 又
∴
∴在[0, 10]和
上各有2个根.
从而方程在
上有800个根, 而
上没有根,
在[2000, 2005]上有2个根.
故方程在上共有802个根. ………16′