高三数学选择填空(七)
1、设![]() ,对于函数
,对于函数![]() ,下列结论正确的是
( B )
,下列结论正确的是
( B )
A.有最大值而无最小值 B.有最小值而无最大值
C.有最大值且有最小值 D.既无最大值又无最小值
2、若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的右焦点重合,则
的右焦点重合,则![]() 的值为
( D )
的值为
( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、平面![]() 的斜线
的斜线![]() 交
交![]() 于点
于点![]() ,过定点
,过定点![]() 的动直线
的动直线![]() 与
与![]() 垂直,且交
垂直,且交![]() 于点
于点![]() ,则动点
,则动点![]() 的轨迹是
( A )
的轨迹是
( A )
(A)一条直线 (B)一个圆 (C)一个椭圆 (D)双曲线的一支
4、设![]() ,则
,则![]() 等于
(
D )
等于
(
D )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5、已知![]() ∈(
∈(![]() ,
,![]() ),sin
),sin![]() =
=![]() ,则tan(
,则tan(![]() )等于
( A )
)等于
( A )
A.![]() B.7
C.-
B.7
C.- ![]() D.-7
D.-7
6、已知︱![]() ︱=1,︱
︱=1,︱![]() ︱=
︱=![]() ,
,![]() =0,点C在∠AOB内,且∠AOC=30°,设
=0,点C在∠AOB内,且∠AOC=30°,设![]() =m
=m![]() +n
+n![]() (m、n∈R),则
(m、n∈R),则![]() 等于
( B )
等于
( B )
A.![]() B.3
C.
B.3
C.![]() D.
D.![]()
7、函数![]() 的定义域是
( B )
的定义域是
( B )
 A.
A.![]() B.
B. ![]() C.
C.
![]() D.
D. ![]()
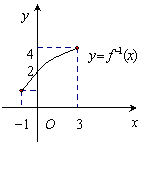
8、函数![]() 的反函数
的反函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]()
(如图所示),则方程![]() 在
在![]() 上的根是
上的根是![]() ( C )
( C )
A.4 B.3 C. 2 D.1
9、已知双曲线![]() (a>0,b<0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
( C
)
(a>0,b<0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
( C
)
A.( 1,2) B.
![]() C.[2,+∞
C.[2,+∞![]() D.(2,+∞)
D.(2,+∞)
10、设过点![]() 的直线分别与
的直线分别与![]() 轴的正半轴和
轴的正半轴和![]() 轴的正半轴交于
轴的正半轴交于![]() 两点,点
两点,点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,![]() 为坐标原点,若
为坐标原点,若![]() 且
且![]() 则点
则点![]() 的轨迹方程是
( D )
的轨迹方程是
( D )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 11、函数
11、函数![]() 对于任意实数
对于任意实数![]() 满足条件
满足条件![]() ,若
,若![]() 则
则![]() ______
______![]() _________。
_________。
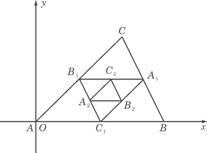
12、如图,连结△ABC的各边中点得到一个新的△A1B1C1,
又连结的△A1B1C1各边中点得到,如此无限继续下去,得
到一系列三角形:△ABC,△A1B1C1,△A2B2C2,…,这一
系列三角形趋向于一个点M,已知A(0,0) ,
B(3,0),C(2,2),则点M的坐标是 ![]() .
.
13、对正整数![]() ,设曲线
,设曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴交点的纵坐标为
轴交点的纵坐标为![]() ,则数列
,则数列![]() 的前
的前![]() 和的公式是
和的公式是 ![]()
 14、
14、![]() 的值为___
的值为___![]() ___。
___。
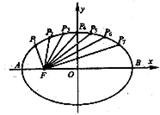
15、如图把椭圆![]() 的长轴AB分成8分,过每个分点作x轴的垂线交椭圆的上半部分于
的长轴AB分成8分,过每个分点作x轴的垂线交椭圆的上半部分于![]() ,
,![]() ,……
,……![]() 七个点,F是椭圆的一个焦点,则
七个点,F是椭圆的一个焦点,则![]() _____35_______.
_____35_______.
16、函数f(x)=的最小值为 90
(附加题)已知![]()
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求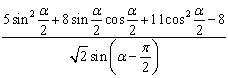 的值。
的值。
选择填空(八)
1、设![]() 是R上的任意函数,则下列叙述正确的是
( )
是R上的任意函数,则下列叙述正确的是
( )
(A)![]() 是奇函数
(B)
是奇函数
(B)![]() 是奇函数
是奇函数
(C) ![]() 是偶函数
(D)
是偶函数
(D) ![]() 是偶函数
是偶函数
2、在等比数列![]() 中,
中,![]() ,前
,前![]() 项和为
项和为![]() ,若数列
,若数列![]() 也是等比数列,则
也是等比数列,则![]() 等于 ( )
等于 ( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D)![]()
3、已知函数![]() ,则
,则![]() 的值域是
( )
的值域是
( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
4、设![]() ,
,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点,
上的一个动点,![]() ,若
,若![]() ,则实数
,则实数![]() 的取值范围是
( )
的取值范围是
( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
|
|
|
|
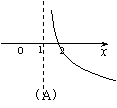 | 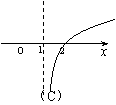 | ||||||||
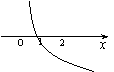 | |||||||||
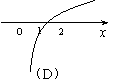 | |||||||||
| |||||||||
6、设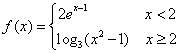 ,则不等式
,则不等式![]() 的解集为
( )
的解集为
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7、已知双曲线![]() ,则双曲线右支上的点
,则双曲线右支上的点![]() 到右焦点的距离与点
到右焦点的距离与点![]() 到右准线的距离之比等于
( )
到右准线的距离之比等于
( )
A.![]() B.
B. ![]() C.
2
D. 4
C.
2
D. 4
8、对于任意的两个实数对![]() 和
和![]() ,规定:
,规定:![]() ,
,
当且仅当![]() ;运算“
;运算“![]() ”为:
”为:
![]() ;运算“
;运算“![]() ”为:
”为:![]() ,设
,设![]() ,若
,若![]() ,则
,则![]() ( )
( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9、已知![]() ,且关于
,且关于![]() 的方程
的方程![]() 有实根,则
有实根,则![]() 与
与![]() 的夹角的取值范围是
( )
的夹角的取值范围是
( )
A.[0,![]() ] B.
] B.![]() C.
C.![]() D.
D.![]()
10、在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,已知
,已知![]() ,则
,则![]() ( )
( )
(A)1 (B)2 (C)![]() (D)
(D)![]()
11、对a,b∈R,记maxa,b=![]() ,函数f(x)=max{x+1,x-2}(x∈R)的最小值是_____________.
,函数f(x)=max{x+1,x-2}(x∈R)的最小值是_____________.
12、已知不等式![]() 对任意正实数
对任意正实数![]() 恒成立,则正实数
恒成立,则正实数![]() 的最小值为
的最小值为
13、函数![]() 的值域是
的值域是
14、已知函数![]() 是定义在实数集上的函数,且
是定义在实数集上的函数,且![]() ,若
,若![]() ,那么
,那么
![]()
15、、对于函数![]() ,给出下列四个命题:①该函数的值域是[—1,1];②当且仅当
,给出下列四个命题:①该函数的值域是[—1,1];②当且仅当![]() 时,该函数取得最大值1;③该函数是以
时,该函数取得最大值1;③该函数是以![]() 为周期的周期函数;④当且仅当
为周期的周期函数;④当且仅当![]() 时,
时,![]() 。以上四个命题中,错误的命题序号是
。以上四个命题中,错误的命题序号是
16、已知向量![]() 满足
满足![]() ,则
,则![]()
(附加题)已知二次函数![]() 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,点
,点![]() 均在函数
均在函数![]() 的图像上。
的图像上。
(Ⅰ)、求数列![]() 的通项公式;
的通项公式;
(Ⅱ)、设![]() ,
,![]() 是数列
是数列![]() 的前n项和,求使得
的前n项和,求使得![]() 对所有
对所有![]() 都成立的最小正整数m;
都成立的最小正整数m;