高三数学一诊模拟考试
数学试题（理科）
第I卷（选择题 共50分）
一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个备选项中，只有一项是符合题目要求的。
1、已知全集
，
，
，则集合
等于（ ）
A、
B、
C、
D、
2、抛物线
的焦点坐标是（ ）
A、
B、
C、
D、
3、在等比数列
中，首项
，则是递增数列的充要条件是公比
满足（ ）
A、
B、
C、
D、
4、以椭圆
的右焦点为圆心，且与双曲线
的渐近线相切的圆的方程是（ ）
A、
B、
C、
D、
5、在锐角
中，若
，则
的取值范围是（ ）
A、
B、
C、
D、
6、关于
的方程
有负实数解，则实数
的取值范围是（ ）
A、
B、
C、
D、
7、已知椭圆
的左右焦点分别为
，过
且倾角为
的直线
交椭圆于A，B两点，对以下结论：①
的周长为8；②
；③在椭圆上不存在相异两点关于直线对称；其中正确的结论有（ ）个
A、3 B、2 C、1 D、0
8、若单调函数
的图象经过点
，则函数
的图象必经过点（ ）
A、
B、
C、
D、
9、直线
与双曲线
的下支交于两个不同的点，则实数
的取值范围是（ ）
A、
B、
C、
D、以上都不是
10、已知抛物线
与轴交于
两点，
在抛物线AB上运动，则
的最大值为（ ）
A、
B、3 C、
D、
第II卷（非选择题 共100分）
二、填空题：本大题共6小题，每小题4分，共24分。把答案填写在答题卡相应的位置上。
11、双曲线
的渐近线方程为
12、不等式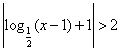
的解集是
13、已知椭圆
的左右焦点分别为，椭圆上一点Q使得
的面积为
，则
的值为
14、已知函数
在
上是减函数，若对于
，有
，且
，则
与
的大小比较关系是
15、当参数
任意取值时，由曲线
上的点在直角坐标平面上所形成的区域的面积是
16、实数
满足约束条件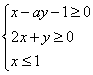
，目标函数
当
时取最大值，则的取值范围是
三、解答题
17、（12分）已知点P
是以原点为中心，焦点在轴上的椭圆C上的一点，P到椭圆的左焦点的距离是3，到左准线的距离是5。（1）求椭圆C的方程；（2）求以椭圆C的焦点为顶点、长轴上的顶点为焦点的双曲线E的方程。
18、（12分）已知函数
，且
（1） 求函数的解析式及其单调递增区间；
（2） 把的图象按向量
平移，所得图象正好关于
轴对称，求
的最小正值。
19、（13分）向量设两个向量
、
，满足
、的夹角为
。
（1）求
和
；（2）若向量
与向量
的夹角为锐角，求实数
的取值范围。
20、（12分）已知数列中，
。数列
的前
项和
。（1）求数列的通项公式。（2）求数列
的前项和。
21、（13分）某城市为了改变交通状况，需进行路网改造，已知原有道路个标段（1个标段是指一定长度的机动车道），拟增建个标段的新路和个道路交叉口，与满足关系
，其中
为常数。设新建1个标段的平均造价为万元，新建1个道路交叉口的平均造价是新建1个标段的平均造价的
倍
，越大，路网越通畅。记路网的堵塞率为
，它与的关系为
。
（1） 写出新建道路交叉口的总造价（万元）与的函数关系；
（2） 若要求路网的堵塞率
，而且新建道路标段为原有道路标段数的25%，求新建的个标段的总造价与新建道路交叉口的总造价之比P的取值范围（用
表示）；
（3） 当
时，在（2）的假设下，要使路网最通畅，且造价比P最高时，问原有道路标段为多少个？
22、（14分）抛物线
的准线与轴的交点为M，过点M作直线交抛物线于A、B两点。
（Ⅰ）求线段AB中点的轨迹方程；
（Ⅱ）若线段AB的垂直平分线交对称轴于点
求证：
；（Ⅲ）若直线的斜率依次取
时，线段AB的垂直平分线与抛物线对称轴的交点依次是
，当
时，求
