高三数学第一学期期中考试
数学试卷
命题人:李修峰
考生在答题前请认真阅读本注意事项及各题答题要求
1、本试卷共2页,包含选择题(第1题至第10题,共10题)、填空题(第11题至第16题,共6题)、解答题(第17题至第21题,共5题)三部分.本次考试时间为120分钟.
2、答题前,请您务必将自己的姓名、考试证号用书写黑色字迹的0.5毫米签字笔填写在试卷及答题卡上.
3、作答必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置,在其它位置作答一律无效.
第Ⅰ卷(选择题,共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出四个选项中,只有一项是符合题目要求的.
1、已知向量![]() ,若
,若![]() ,则
,则![]() 的值分别等于
( )
的值分别等于
( )
A、1,0 B、1,1 C、0,1 D、—1,0
2、已知![]() 是定义在R上的奇函数,则
是定义在R上的奇函数,则![]() 的值是
( )
的值是
( )
A、2
B、![]() C、
C、![]() D、
D、![]()
3、已知函数![]() ,则
,则![]() 等于
( )
等于
( )
A、![]() B、—
B、—![]() C、
C、![]() D、—
D、—![]()
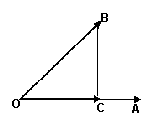
4、如图,非零向量![]() ,且
,且![]() ,C为垂足,设向量
,C为垂足,设向量![]() ,则
,则![]() 的值为
( )
的值为
( )
 A、
A、![]() B、
B、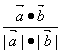
C、![]() D、
D、![]()
5、函数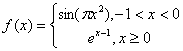 若
若![]() ,则
,则![]() 的所有可能值组成的集合为( )
的所有可能值组成的集合为( )
A、![]() B、
B、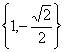 C、
C、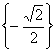 D、
D、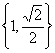
6、若函数![]() 的图象按向量
的图象按向量![]() 平移后,得到的图象关于原点对称,则向量
平移后,得到的图象关于原点对称,则向量![]() 可以是 ( )
可以是 ( )
A、![]() B、(
B、(![]() C、
C、![]() D、
D、![]()
7、若函数![]() 的最小正周期为1, 则它的图象的一个对称中心为
的最小正周期为1, 则它的图象的一个对称中心为
( )
A、
![]() B、
B、 ![]() C、
C、![]() D、
D、![]()
8、已知A、B、C是平面上不共线的三点,O为△ABC的外心,动点P满足![]()
![]() ,则动点P的轨迹一定通过△ABC的
( )
,则动点P的轨迹一定通过△ABC的
( )
A、内心 B、垂心 C、重心 D、AB边的中点
9、已知下列四个函数及它们的大致图象,则解析式与图象对应关系判断正确的是
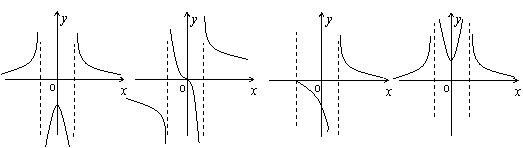 |

a b c d
①![]() ②
②![]() ③
③![]() ④
④![]()
A.①a②d③b④c B. ①d②b③a④c C. ①d②a③b④c D. ①d②c③b④a
10、设定义域为![]() 的函数
的函数![]() 满足
满足![]() 且
且![]() ,则
,则
![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题,共100分)
二、填空题:本大题共6小题,每小题6分,共36分.把答案填在答卷纸相应位置上.
11、若![]() ,且
,且![]() ,则向量
,则向量![]() 与
与![]() 的夹角为
▲
的夹角为
▲
12、设周期为4的奇函数![]() 的定义域为R, 且当
的定义域为R, 且当![]() 时,
时, ![]() , 则
, 则![]() 的值为
▲
.
的值为
▲
.
13、已知数列![]() 的首项
的首项![]() 是其前
是其前![]() 项的和,且满足
项的和,且满足![]() ,则此数列的通项公式为
,则此数列的通项公式为![]() ▲
▲
14、在△ABC中,![]() ,则△ABC的面积的最大值为 ▲
,则△ABC的面积的最大值为 ▲
15、符号![]() 表示不超过
表示不超过![]() 的最大整数,如
的最大整数,如![]() ,定义函数
,定义函数![]() ,那么下列命题中正确的序号是 ▲ .
,那么下列命题中正确的序号是 ▲ .
(1)函数![]() 的定义域为R,值域为
的定义域为R,值域为![]() ; (2)方程
; (2)方程![]() ,有无数解;
,有无数解;
(3)函数![]() 是周期函数;
(4)函数
是周期函数;
(4)函数![]() 是增函数。
是增函数。
16、对于定义域为实数集R的两个函数![]() ,如果函数
,如果函数![]() 的图象始终在函数
的图象始终在函数![]() 图象的上方,则称函数
图象的上方,则称函数![]() 可被函数
可被函数![]() 覆盖。下列三个函数:
覆盖。下列三个函数:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 。其中可被
。其中可被![]() 覆盖的所有函数是 ▲ (写出序号)。
覆盖的所有函数是 ▲ (写出序号)。
三、解答题:本大题共4小题,共54分.请把解答写在答题卷规定的答题框内.解答应写出文字说明、证明过程或演算步骤.
17、已知向量a=(![]() ),b=(
),b=(![]() ),c=(-1,0),d=(0,1).
),c=(-1,0),d=(0,1).
(1)求证:a⊥(b+c);
(2)设![]() a·(b- d),且
a·(b- d),且![]() ,求
,求![]() 的值域.
的值域.
18、已知向量![]() .
.
(1)若点A、B、C能构成三角形,求实数m应满足的条件;
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值.
19、把正奇数数列![]() 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
1
3 5
7 9 11
— — — —
— — — — —
设![]() 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第![]() 行、从左往右数第
行、从左往右数第![]() 个数。
个数。
(I)若![]() ,求
,求![]() 的值;
的值;
(II)已知函数![]() 的反函数为
的反函数为![]()
![]() ,若记三角形数表中从上往下数第n行各数的和为
,若记三角形数表中从上往下数第n行各数的和为![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() 。
。
 20、已知:
20、已知: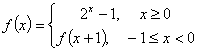
(1)分别求![]() 、
、![]() 的值。
的值。
(2)求当![]() 时,
时,![]() 的表达式。
的表达式。
(3)画出函数![]() 的图象。
的图象。
(4)若![]() 至多只有一个解,求
至多只有一个解,求![]() 的取值范围。
的取值范围。
21、已知函数![]() 在区间[n,m]上为减函数,记m的最大值为m0,n的最小值为n 0,且有m0- n 0=4.
在区间[n,m]上为减函数,记m的最大值为m0,n的最小值为n 0,且有m0- n 0=4.
(1)求m0,n 0的值以及函数![]() 的解析式;
的解析式;
(2)已知等差数列{xn}的首项![]() ,公差
,公差![]() .又过点
.又过点![]() 的直线方程为
的直线方程为![]() 试问:在数列{xn}中,哪些项满足
试问:在数列{xn}中,哪些项满足![]() ?
?
(3)若对任意![]() ,都有
,都有![]() 成立,求a的最小值.
成立,求a的最小值.