高三数学调研试卷(二)
一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．中国数学教育网 http://www.mathedu.cn
1．不等式
的解集是
A．
B．
C．
D．
2．等比数列{an}中，a2＋a6＝24，a3a5＝64，则a4＝
A．±8 B．±16 C．－8 D．8
3．向量a = （1，2），b = （x，1），c = a + b，d = a − b，若c//d，则实数x的值等于
（A）
（B）
（C）
（D）
4. 抛物线y=4x2上的一点P到焦点的距离为1，则点P的纵坐标为
A. 
B.
0
C. 
D.
5．三个学校分别有1名、2名、3名学生获奖，这6人排成一排合影，要求同校任两名学生不能相邻，那么不同的排法有
A、36种 B、72种 C、108种 D、120种
6．某单位准备用不同花色的装饰石材分别装饰办公楼中的办公室、走廊、大厅的地面及楼的外墙．现有编号为1～6的6种不同花色石材可供选择，其中1号石材有微量的放射性，不可用于办公室内，则不同的装饰效果共有
A．350种 B．300种 C．65种 D．50种
7．以椭圆
的右焦点
为圆心，
为半径的圆与椭圆的右准线交于不同的两点，则该椭圆的离心率的取值范围是
A、
B、
C、
D、
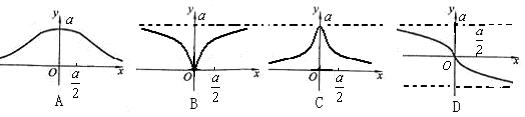
8．在直角坐标系中,函数
所表示的曲线叫箕舌线，则箕舌线可能是下列图形中的
9．下列命题中，正确的个数是
①若＋＝0，则＝＝；
②在△ABC中，若＋＋＝，则O为△ABC的重心；
③若，是共线向量，则·＝·，反之也成立；
④若，是非零向量，则＋＝的充要条件是存在非零向量，使·＋·＝0．
A．1 B．2 C．3 D．4
10．实系数方程x2＋ax＋2b＝0的一个根大于0且小于1，另一个根大于1且小于2，则的取值范围是
A．(－，) B．(，1) C．(，1) D．(－，)
二、填空题：本大题共6小题，每小题5分，共30分．把答案填在答题卷相应位置上．
11、
的展开式中，系数最大的项是第______项;
12．二项式
的展开式中的常数项是 ；
13．若a1(x－1)4＋a2(x－1)3＋a3(x－1)2＋a4(x－1)＋a5＝x4，则a2－a3＋a4＝ ；
14．已知集合A＝{1,2,3}，B＝{－1,0,1}，满足条件f(3)＝f(1)＋f(2)的映射f：A→B的个数是 ；
15．P(x,y)是由y=x，y=－x，x=2三条直线所围成的三角形内部一个动点，且P到这三条直线的距离依次为PE、PF、PH，且PE·PF=PH2，则P的轨迹方程是____________；
16.已知椭圆与双曲线
有相同的焦点（-c,0）,(c,0).若c是a,m的等比中项，n2是2m2,c2的等差中项，则椭圆的离心率是 ；
17.现有3人从装有编号为1，2，3，4，5的五个小球的暗箱中每人摸出一只球（摸后不放回）,则有两人所摸的小球编号是连号,且三人编号不连号的摸法种数为 ；
18．在实数的原有运算法则中，我们补充定义新运算“＋”如下：当a≥b时，a＋b＝a；当a＜b时，a＋b＝b2；则函数f(x)＝(1＋x)·x―(2＋x)，x∈[―2,2]的最大值等于 。 (“·”与“－”分别为乘法与减法)．
三、解答题：（本大题5个小题，共70分）各题解答必需答在答题卡Ⅱ上（必需写出必要
的文字说明、推理过程或计算步骤）。
19．已知 A、B 、C为ΔABC的三个内角，
，
.
（Ⅰ）若
求角A； （Ⅱ）若
，求
.
20．已知等差数列{an}的前n 项之和为Sn，令bn=
，且a4b4=
，S6−S3=15．
（Ⅰ）求数列{bn}的通项公式及它的前10项之和；
（Ⅱ）若c1=1，cn+1−cn=0，Tn=
，求Tn ．
21．（文科做1-8）已知A(－2,0)，B(2,0)，点C、D满足＝2，＝(＋)．
(1)求点D的轨迹方程；
(2)过点A作直线L交以A、B为焦点的椭圆于M、N两点，线段MN的中点到y轴的距离为，且直线L与点D的轨迹相切，求该椭圆的方程．
21．（理科做9-22）在平面直角坐标系中，已知A1（−3，0）、A2（3，0）、P（x，y）、M（
，0），若实数l使向量
、l
、
满足l2·
=·．
（Ⅰ）求P点的轨迹方程，并判断P点的轨迹是怎样的曲线；
（Ⅱ）当l=
时，过点A1且斜率为1的直线与（Ⅰ）中的曲线相交的另一点为B，能否在直线x=−9上找一点C，使△A1BC为正三角形．
22．已知双曲线c的中心在原点，抛物线y2＝8x的焦点是双曲线C的一个焦点，且双曲线c过点(,)．
(1)求双曲线C的方程；
(2)设双曲线C的实轴左顶点为A，右焦点为F，在第一象限内任取双曲线C上一点P，试问是否存在常数λ(λ＞0)使得∠PFA＝λ∠PAF恒成立？并证明你的结论．