高三数学复习综合检测
一 选择题:(本大题共10小题, 每小题5分,共50分)
1.已知集合M=![]() ,
,![]() ,则M
,则M![]() =
( )
=
( )
A . ![]() B. R
C. M
D. N
B. R
C. M
D. N
2. 设![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.-9
D.-9
3. 若![]()
![]() ,则
,则![]() 恒成立的 ( )
恒成立的 ( )
A.充要条件 B.充分不必要条件 C.必要不充分条件 D. 既不充分也不必要条件
4.![]() ( )
( )
A. 1
B.-1
C. 1或-1
D.与![]() 大小及BC的长有关
大小及BC的长有关
5.设![]() 的两个焦点,点P在双曲线上且
的两个焦点,点P在双曲线上且![]()
![]() ,则
,则![]() 的值
( )
的值
( )
A. ![]() B.
B.
![]() C. 1
D.2
C. 1
D.2
6.已知![]() 是方程
是方程![]() 的两根,且
的两根,且![]() ,则
,则![]() ( )
( )
A.![]() B .
B .![]() C.
C. ![]() D.
D.
![]()
7.若![]() ,则
,则![]() 的取值范围是
( )
的取值范围是
( )
A. 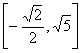 B.
B.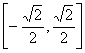 C.
C. 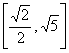 D.
D.![]()
8. 已知直角坐标系中的四点P(0,2),Q(0,-2),R(3,-8),S(![]() )(
)(![]() )沿x轴将坐标平面折成大小为θ的二面角,则
( )
)沿x轴将坐标平面折成大小为θ的二面角,则
( )
A.P,Q,R,S四点共面 B. P,Q,R,S四点必不共面
C. P,Q,R,S四点是否共面取决于Q.
D. P,Q,R,S四点是否共面取决于![]()
9.已知不等式![]() 对于任意正实数x,y都成立,则正实数a的最小值为( )
对于任意正实数x,y都成立,则正实数a的最小值为( )
A.8 B.6 C. 4 D. 2
10.已知定义在R上的函数![]() 的导函数
的导函数![]() 在R上也可导,且
在R上也可导,且![]() <0,则
<0,则![]() ( )
( )
A. ①② B.①③ C.②③ D.③④
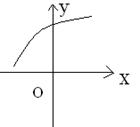
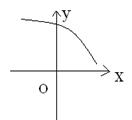
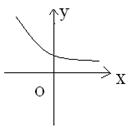
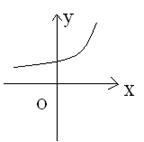
① ② ③ ④
二.填空题 (本大题共6小题;每小题5分,共30分)
11.二项式![]() 的展开式中
的展开式中![]() 的系数是_______________.
的系数是_______________.
12.函数f(x)=x3+ax2+bx+a2 在x=1时有极值10,则 ![]() .
.
13.正方形ABCD-A1B1C1D1的棱长为a,O为底面A1B1C1D1中心,P为棱B1C1上任一点,则P到面OBC的距离为________________
14.已知数列![]() 的通项公式为
的通项公式为![]() ,则
,则![]() =__
=__
15.一项“过关游戏”规则规定:在第n关要抛掷一颗骰子n次,如果这n次抛掷所出现的点数之和大于n2,则算过关,那么,连过前二关的概率是_______..
16.若一系列函数的解析式相同,值域相同,但定义域不同,则称这一系列函数为“同簇函数”,问:解析式y=x2,值域为{1,2}的同簇函数共有__________个
三 解答题:(本大题5小题,共70分)
17.(本题12分)已知![]()
(1)求函数![]() 的最小正周期T及单调增区间。(2)当
的最小正周期T及单调增区间。(2)当![]() 时,函数
时,函数![]() 的最小值为2,求此时函数
的最小值为2,求此时函数![]() 的最大值,并指出
的最大值,并指出![]() 取到最大值。
取到最大值。
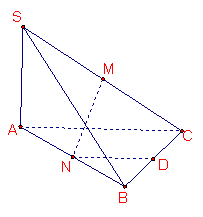 18.(本题14分)如图,三棱锥S-ABC中,SA⊥平面ABC,∠ABC=
18.(本题14分)如图,三棱锥S-ABC中,SA⊥平面ABC,∠ABC=![]() ,SA=BC=2,AB=4,M,N,D分别是SC,AB,BC的中点.
,SA=BC=2,AB=4,M,N,D分别是SC,AB,BC的中点.
![]()
![]()
![]()
![]()
19.(本题14分)已知椭圆![]() 的方程为
的方程为![]() ,双曲线
,双曲线![]() 的左,右焦点分别为
的左,右焦点分别为![]() 的左,右顶点,而
的左,右顶点,而![]() 的左,右顶点分别
的左,右顶点分别![]() 的左,右焦点.
的左,右焦点.
(1)求双曲线![]() 的方程
的方程
(2)若直线![]() 与椭圆
与椭圆![]() 及双曲线
及双曲线![]() 都恒有两个不同的交点,且
都恒有两个不同的交点,且![]() 的两个交点
的两个交点![]() 满足
满足![]() (其中O为原点),求k取值范围.
(其中O为原点),求k取值范围.
20. (本题14分)已知函数![]()
![]()
![]()
21.(本题16分)数列![]()
(1)若数列![]()
(2)求数列![]() 的通项公式
的通项公式![]()
(3)数列![]() 适合条件的项;若不存在,请说明理由
适合条件的项;若不存在,请说明理由