高三数学复习综合检测
一 选择题:(本大题共10小题, 每小题5分，共50分)
1．已知集合
( )
A. {0} B.{0,1} C.{1,2} D.{0,2}
2. 命题“若
，则
”的逆否命题是
( )
A．若
，则
B．若，则
C．若a ≤b，则
D．若，则a ≤b
3.等差数列
的各项是负数且
，那么它的前10项和
= （ ）
A． -9 B．-11 C． -13 D．-15
4．已知函数
的解集是
( )
A. 
B.(1,2) C.
D.
5.要得到y=sinx-cosx的图象，可以把y=sinx+cosx的图象向右平移 （ ）
A．
B．
C．
D．
6．5个人站一排，甲，乙两人中间恰有一个人的不同站法的种数有 （ ）
A．288 B．72 C．36 D．24
7.若圆x2+ y2 －4
x －4y=0上只有一个点到直线m: ax+by=0的距离为
,则直线m的倾斜角为
( )
A . 
B.
C.
D.
8．已知点A
的平分线AE与BC相交与E，那么有
其中
等于
（ ）
A．0.5 B．1.5 C． 3.5 D．5
9.在椭圆
上有一点P,
是椭圆的左右焦点,
为直角三角形,则这样的点P有
( )
A. 2个 B. 4个 C.6个 D.8个
10．某商场宣传在“十一黄金周”期间对顾客购物实行一定的优惠，商场规定：
①如一次性购物不超过200元，不予以折扣；
②如一次性购物超过200元但不超过500元的，按标价给予九折优惠；
③如一次性购物超过500元的，其中500元给予9折优惠，超过500元的部分给予八五折优惠．
某人两次去购物，分别付款176元和432元，如果他只去一次购买同样的商品，则应付款 ( )
A．608元 B．574.1元 C．582.6元 D．456.8元
二．填空题 (本大题共6小题；每小题5分，共30分)
11. 某中学有高一学生400人，高二学生300人，高三学生300人，现通过分层抽样抽取一样本容量为n的样本，已知每个学生被抽到的概率为0.2，则
________
12.已知函数
是奇函数,则a=_______________
13.已知向量
，
，若
等于________
14. 设地球O的半径为R，P和Q是地球上两点，P在北纬
，东经
，Q在北纬，东经
，则P与Q两地的球面距离为_____________
15. 一个四面体的所有棱长都为
，四个顶点在同一球面上，则此球的表面积为_______.
16．设有两个命题：①关于x的不等式
的解集是R，②函数
是减函数．如果这两个命题中有且只有一个真命题，则实数m的取值范围是
三 解答题：(本大题5小题，共70分)
17.（本题12分）甲乙两支球队进行五局三胜制的比赛，规定一方胜满三局即结束比赛，且在每场比赛中甲乙获胜的概率均为
，最终甲获胜的概率记为
，且
,
(1)求的值； （2）求
的值 (3)求
的值
18．（本题12分）已知双曲线
=1(a＞0,b＞0)的离心率e=2.过点A(0，-b)和B(a,0)的直线与原点的距离为 
.
(1) 求双曲线的方程；
(2)直线
∶y=kx+ (k≠0)与双曲线交于不同两点C、D.当OC⊥OD时，求k的值.
19.
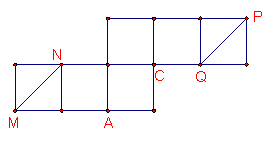
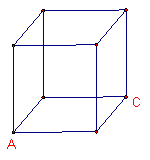
图(1)是正方体的表面展开图,MN和PQ是两条面对角线,请在图(2)的正方体中将MN和PQ画出来,并就这个正方体解答下列各题.
(1)求MN和PQ所成的角;
(2)求四面体NMPQ的体积与正方体的体积之比;
(3)求二面角M-NQ-P的大小.
20.（本题满分14分）
函数
在
与
上单调性相同，在
与上单调性相反。（1）求c的值；（2）当
为何值时，
取得极值？并判断出这些极值点的横坐标与2、4的大小关系；（3）的图象上是否存在点
使f(x)在M处的切线斜率为
？
21．(本题16分) 数列
(1)求数列的通项公式;
(2)设
(3)设
.是否存在最大的整数m,使得对任意的
成立?若存在,求出m的值,若不存在,请说明理由.