高三数学复习综合检测
一．选择题：(本大题共12小题；每小题5分，共60分)
1.定义
，若
，
则
= （ ）
A. A, B. B
C.{1,7,9}
D.{2},
2.若奇函数
有反函数,则下列各点中，一定在
的图象上的点是A. 
B . 
C
D. 
( )
3.已知两点
,P是线段AB上的点,且
,则点P到直线3x+4y-18=0的距离是————————————————————————————————( )
A. 
B.
C.
D.
4.若
是
”的
(
)
A.充分不必要条件 B.必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
5.在约束条件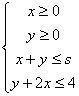
下,当
时,目标函数
的最大值的变化范围是
A.
B. 
C. 
D. 
( )
6.已知实系数一元二次方程
的解集为φ则函数
的值域为——————————————————————————（ ）
A.
B.
C.
D.
7.若
是
上的奇函数,方程=0的解集为
,则
的值是( )
A.
B.0
C.3
D.不确定
8.已知a=(λ,2),b=(-3,5)且a与b所成的角为钝角，则λ的取值范围是———————( )
A.
B
C.
D.
9．
曲线
（ ）
A． 
B．
C．
D．
10.若异面直线a,b所成的角为
，且直线c⊥a,则异面直线b,c所成的角的范围是———( )
A.
B. 
C.
. D. 
二.填空题(本大题共6小题；每小题5分，共30分)
11.已知数列
满足
，则数列的通项公式为__________
12．不等式
恒成立，则实数
的取值范围为___________.
13.已知斜三棱柱
,侧面
是边长为3的正方形，
到侧面的距离为2, E为侧棱
上一点，且
,则三棱锥
的体积为____________.
14 .把一个函数的图像按向量a=(3，-2)平移，得到的图像的解析式为y=log2(x+3)+2，则原来的函数的解析式为_________________________.
15.一系列椭圆都以一定直线
为准线,所有椭圆的中心都在定点M,且点M到的距离为2,若这一系列椭圆的离心率组成以
椭圆相应的长半轴长为
=_______________
16.函数
的图像与直线x=a,x=b及x轴所围成图形的面积称为函数在
上的面积，已知函数
在
上的面积为
，则
⑴函数
在
上的面积为_______________
(2)函数
在
的面积为_____________.
三．解答题(本大题5小题，共60分)
17．（本题满分10分）已知锐角△ABC中,角A、B、C的对边分别是a、b、c,tanB=
⑴求角B的大小；
⑵求sin(B+10
)[1-
]的值.
18．（本题满分12分）已知函数
在x=
时都取得极值.
⑴求a、b的值及函数
的单调区间；
⑵若对
，不等式
恒成立，求c的取值范围.
19．（本题满分16分）如图:在直角梯形ABCP中，BC∥AP，AB⊥BC，CD⊥AP，AD=DC=PD=2，E、F、G分别是线段PC、PD、BC的中点，现将△PDC折起，使平面PDC⊥平面ABCD
⑴ 求证：AP∥平面EFG；
⑵求二面角G-EF-D的大小；
⑶在线段PB上确定一点Q，使PC⊥平面ADQ,给出证明.
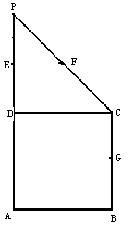
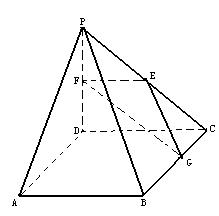
⑴ ⑵
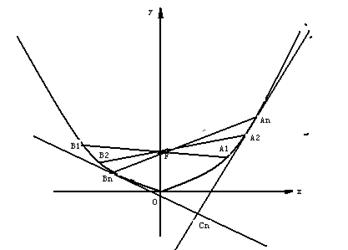
20、（本题满分16分）如图：对每个正整数n，
是抛物线
上的点，过焦点F的直线
，交抛物线于另一点
.
⑴试证：
⑵取
并记
为抛物线上分别以
为切点的两条切线的交点.试证:
21．（本题满分16分）
在直角坐标系中,已知向量
,
(
),
的最小值为1,
动点P同时满足下列三个条件:⑴
;⑵
⑶动点P的轨迹C经过点B(0,-1)
㈠求曲线C的方程; ㈡是否存在方向向量m=(1,k)(k
)的直线L,L与曲线C相交于M、N两点，使
，且
与
的夹角为
？若存在，求出k，并求出直线L的方程；若不存在，请说明理由.