高三数学基础训练（19）
（理科）
班别____________ 姓名_____________ 座号 ___________ 评分 _________
一、选择题：在每小题给出的四个选项中,只有一个符合题目要求的。（每题5分,共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1．设 
是两个平面， 
是两条直线，下列命题中，可以判断 
的是
A． 
且 
B． 
且 
C． ， 
且 
D． 
， 
且
2．下列说法不正确的是
（1）一条直线垂直于一个平面内的无数条直线，则这条直线和这个平面垂直；
（2）经过一点和一条已知直线垂直的直线都在同一平面内；
（3）一个平面内不可能有直线与这个的一条斜线垂直；
（4）如果直线a//平面α，直线b⊥a，则b⊥平面α。
A .（2） B.（1）（3） C.（1）（2）（3） D.（ 1）（3）（4）
3．设P是△ABC所在平面外一点，P到△ABC各顶点的距离相等，而且P到△ABC各边的距离也相等，那么△ABC
A 是非等腰的直角三角形 B 是等腰直角三角形
C 是等边三角形 D 不是A、B、C所述的三角形
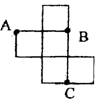
4．如图，是一个无盖正方体盒子的表面展开图，A、B、C为其上
的三个点，则在正方体盒子中，∠ABC等于
A．45° B．60° C．90° D．120°
5．一个正方形的直观图是一个平行四边形，其中一边长为4，则此正方形的面积是
A．16 B．64 C．16或64 D．都不对
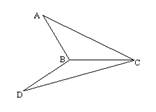6.设△ABC和△DBC所在两平面互相垂直，
且AB=BC=BD=a,∠CBA=∠CBD=120°,
则AD与平面BCD所成的角为
A.30° B.45°
C.60° D.75°
7．短轴长为
，离心率
的椭圆两焦点为F1，F2，过F1作直线交椭圆于A、B两点，则△ABF2的周长为
A．3 B．6 C．12 D．24
8．一直线和直二面角的两个面所成的角分别是
，则
的范围是
9．正方体
中，
、
、
分别是
、
、
的中点．那么，正方体的过、、的截面图形
A．三角形 B．四边形 C．五边形 D．六边形
10．过原点的直线与圆
相切，若切点在第二象限，则该直线的方程是
A．
B．
C．
D． 
11．已知向量
和向量
的夹角为
，
，
，那么
（ ）
A．
B．
C．
D．
12．过抛物线
的焦点的直线交抛物线于A、B两点，O为坐标原点，则
的值是
A．3 B．－3 C．12 D．－12
二、填空（把答案填在题中横线上，每题5分，共40分）
13．在正方体
中，
、
分别是棱
和的中点，为底面
的中心，则直线
与
所成的角为
.
14．体积为
的正方体内接于球，则该球的体积为
.
15．定义运算
，若实数x满足
16．若异面直线
所成的角为
，且直线
，则异面直线
所成角的范围是____
17．下面有四个命题：
①若
、
为一平面内两非零向量，则
的充要条件；
②一平面内两条曲线的方程分别是
，它们的交点是
，则方程
的曲线经过点P；
③经过一定点且和一条已知直线垂直的所有直线都在同一平面内；
. 其中真命题的序号是 （把符合要求的命题序号都填上）.
18．过点
(1，2)的直线l将圆
分成两段弧，其中的劣弧最短时，l的方程为 ．
19．过抛物线的焦点F作直线
与抛物线交于P（
、
两点，
，则
=
.
20. 实数
，则
的最大值为
.
高三数学基础训练（19）答案
（理科）
DDCBC BBDDA DB
13．60°
14. 
15.
1或3
16. 
17
①②③ 18． 
19 . 8
20. 1+
6解析：作AO⊥CB的延长线，连OD，则OD即为AD在平面BCD上的射影，
∵AO=OD=
a,∴∠ADO=45°.
高三数学基础训练（19）答案
（理科）
DDCBC BBDDA DB
13．60°
14. 15.
1或3
16.
17
①②③ 18． 19 . 8
20. 1+
6解析：作AO⊥CB的延长线，连OD，则OD即为AD在平面BCD上的射影，
∵AO=OD=a,∴∠ADO=45°.