高考数学招生全国统一考试数 学
第1卷(选择题 60分)
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项符合题目要求的．
（1）函数
的最小正周期是
（A）
（B）p （C）2p （D）4p
（2）圆(x－1)2＋y2=1的圆心到直线y=
x的距离是
（A）
（B）
（C）1 （D）
（3）不等式(1＋x)(1－
)＞0的解集是
（A）｛
0≤x≤1｝ （B）｛x＜0 且x≠－1｝
（C）｛－1＜x＜1｝ （D）｛ x＜1且x≠－1｝
（4）在(0，2p)内，使sinx＞cosx成立的x取值范围为
（A）(
，)∪(p，
) （B）(，p)
（C）(，) （D）(，p)∪(，
)
（5）设集合M=
，N=
，则
（A）M=N （B）MÌN （C）MÉN （D）M∩N=f
（6）一个圆锥和一个半球有公共底面，如果圆锥的体积恰好与半球的体积相等，那么，这个圆锥轴截面顶角的余弦值是
（A）
（B）
（C）
（D）－
（7）函数f(x)=x
＋b是奇函数的充要条件是
（A）ab=0 （B）a＋b=0 （C）a=b （D）a2＋b2=0
（8）已知0＜x＜y＜a＜1则有
（A）loga(xy)＜0 （B）0＜loga(xy)＜1
（C）1＜loga(xy)＜2 （D）loga(xy)＞2
（9）函数
（A）在(－1，＋∞)内单调递增 （B）在(－1，＋∞)内单调递减
（C）在(1，＋∞)内单调递增 （D）在(1，＋∞)内单调递减
（10）极坐标方程r=comq与r com=
的图形是
（11）从正方体的6个面中选取3个面，其中有2个面不相邻的选法共有
（A）8种 （B）12种 （C）16种 （D）20种
（12）据2002年3月5日九届人大五次会议（政府工作报告）：“2001年国内生产总值达到95933亿元，比上年增长7.3%．”如果“十五”期间（2001—2005年）每年的国内生产总值都按此年增长率增长，那么到“十五”末我国国内年生产总值为
（A）115000亿 （B）120000亿 （C）127000亿 （D）135000亿
第II 卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上．
（13）椭圆5x2＋ky2=5的一个焦点是（0，2），那么k=_________．
（14）(x2＋1)(x－2)7的展开式中x3项的系数是_____________．
（15）已知sina=cos2a (a∈ (
，p))，则tga=_______
（16）已知f(x)=
，那么f(1)＋f(2)＋f()＋f(3)＋f(
)＋f(4)＋f(
)=_____．
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤．
（17）（本小题满分12分）
已知复数z=1＋i，求实数a，b使az＋2b
=(a＋2z)2．
（18）（本小题满分12分）
设｛an｝为等差数列，｛bn｝不等比数列，a1= b1=1，a2＋a4= b3，b2 b4= a3，分别求出｛an｝及｛bn｝的前10项的和S10及T10
（19）（本小题满分12分）
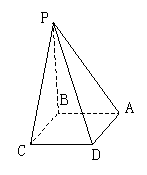
四棱锥P-ABCD的底面是边长为a的正方形，PB⊥面ABC（D）
（I）若面PAD与面ABCD所成的二面角为60°，求这个四棱锥的体积；
（II）证明无论四棱锥的高怎样变化，面PAD与面PCD所成的二面角恒大于90°．
（20）（本小题满分12分）
设A、B是双曲线
上的两点，点N（1，2）是线段AB的中点．
（I）求直线AB的方程
（II）如果线段AB的垂直平分线与双曲线相交于C、D两点，那么A、B、C、D四点是否共圆？为什么？
（21）（本小题满分12分，附加题4分）
（I）给出两块面积相同的正三角形纸面（如图1，图2），要求用其中一块剪拼成一个正三棱锥模型，另一块剪拼成一个正三棱柱模型，使它们的面积都与原三角形的面积相等，请设计一种剪拼方法，分别用虚线标示在图1、图2中，并作简要说明；
（II）试比较你剪拼的正三棱锥与正三棱柱的体积大小；
（III）（本小题为附加题，如果解答正确，加4分，但全卷总分不超过150分）
如果给出的是一块任意三角形的纸片（如图3），要求剪拼成一个直三棱柱模型，使它的全面积与给出的三角形的面积相等，主设计一种剪拼方法，用虚线标示在图3中，并作简要说明．
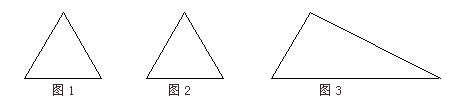
（22）（本小题满分14分）
已知a＞0，函数f(x)=ax－bx2
（I）当b＞0时，若对任意x∈R都有f(x)≤1，证明a≤2
；
（II）当b＞1时，对任意x∈[0，1]，
≤1的充要条件是b－1≤a≤
；
（III）当0＜b≤1时，讨论：对任意x∈[0，1]，≤1的充要条件．
普通高等学校招生全国统一考试
数学参考答案
一、选择题：本题考查基本知识和基本运算。每小题5分，满分60分。
（1）C （2）A （3）D （4）C （5）B （6）C
（7）D （8）D （9）C （10）B （11）B （12）C
二、填空题：本题考查基本知识和基本运算，每小题4分，满分16分。
（13）1 （14）1008 （15）
（16）
三、解答题
（17）满分12分
解：∵ z=1＋i，
∴ 
因为a，b都是实数，
所以由 
得
两式相加，整理得
a2＋6a＋8=0
解得 a1=－2，a2=－4
对应得 b1=－1，b2=2
所以，所求实数为 a=－2，b=－1或a=－4，b=2
（18）满分12分
解：∵ {an}为等差数列，{bn}为等比数列，
∴ a2＋a4=2a3，
已知 a2＋a4=b3，b2b4=a3，
∴ b3=2a3，
得 
∵ b3≠0 ∴ 
由a1=1，
知{an}的公差为
∴ 
由b1=1，
知{bn}的公比为
或
。
当 时，
，
当 时，
。
（19）满分12分。
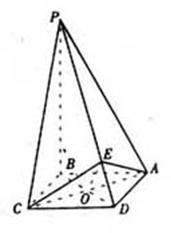
（I）解：∵ PB⊥面ABCD，
∴ BA是PA在面ABCD上的射影，
又 DA⊥AB，
∴ PA⊥DA，
∴ ∠PAB是面PAD与面ABCD所成的二面角的平面角，
∴ ∠PAB=60°
而PB是四棱锥P－ABCD的高，PB=AB·
∴ 
（II）证：不论棱锥的高怎样变化，棱锥侧面PAD与PCD恒为全等三角形。
作AE⊥DP，垂足为E，连结EC，则△ADE
△CDE，
∴ AE=CE，∠CED=90°，故∠CEA是面PAD与面PCD所成的二面角的平面角。
设AC与DB相交于点O，连结EO，则EO⊥AC，
∴ 
在△AEC中，
所以，面PAD与PCD所成的二面角恒大于90°。
（20）满分12分。
解：（I）依题意，可设直线AB的方程为 y=k(x－1)＋2，
代入 
，整理得
①
记A(x1，y1)，B(x2，y2)，x1，x2则是方程①的两个不同的根，所以2－k2≠0，且
，
由N(1，2)是AB的中点得
，
∴ k(2－k)=2－k2，
解得k=1，所以直线AB的方程为
y=x＋1
（II）将k=1代入方程①得x2－2x－3=0
解出 x1=－1，x2=3
由 y=x＋1得 y1=0，y2=4。
即A、B的坐标分别为(－1，0)和(3，4)。
由CD垂直平分AB，得直线CD的方程为
y=－(x－1)＋2，
即 y=3－x。
代入双曲线方程，整理得 x2＋6x－11=0。 ②
记C(x3，y3)，D(x4，y4)，以及CD的中点为M(x0，y0)，则x3，x4是方程②的两个根。所以x3＋x4=－6，x3x4=－11。
从而 
∴ 
又 
即A、B、C、D四点到点M的距离相等，所以A、B、C、D四点共圆。
（21）满分12分，附加题4分。
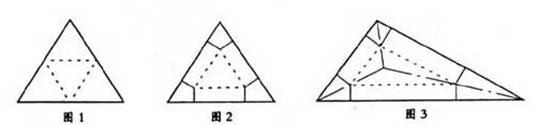
解：（I）如图1，沿正三角形三边中点连线折起，可拼得一个正三棱椎。
如图2，正三角形三个角上剪出三个相同的四边形，其较长的一组邻边边长为三角形边长的
，有一组对角为直角。余下部分按虚线折起，可成为一个缺上底的正三棱柱，而剪出的三个相同的四边形恰好拼成这个正三棱柱的上底。
（II）依上面剪拼的方法，有V柱＞V锥。
推理如下：
设给出正三角形纸片的边长为2，那么，正三棱锥与正三棱柱的底面都是边长为1的正三角形，其面积为
，现在计算它们的高：
∴ 
所以 V柱＞V锥。
（III）（附加题，满分4分）
如图3， 分别连结三角形的内心与各顶点，得到三条线段，再以这三条线段的中点为顶点作三角形，以新作的三角形为直三棱柱的底面，过新三角形的三个顶点向原三角形三边作垂线，沿六条垂线剪下三个四边形，可以拼接成直三棱柱的上底，余下部分按虚线折起，成为一个缺上底的直三棱柱，即可得到直三棱柱的模型。
（22）满分14分。
（I）证：依设，对任意x∈R，都有f(x)≤1，
∵f(x)=
，∴
≤1，
∵a＞0，b＞0，∴a≤2。
（II）证：
必要性
对任意x∈[0，1]，≤1 Þ －1≤f(x)，据此可以推出－1≤f(1)，
即 a－b≥－1，∴a≥b－1；
对任意x∈[0，1]，≤1 Þ f(x)≤1，因为b＞1，可以推出
≤1，
即a·
－1≤1，
∴a≤2；
∴b－1≤a≤2。
充分性
因为b＞1，a≥b，对任意x∈[0，1]，可以推出
ax－bx2≥b(x－x2)－x≥－x≥－1，
即 ax－bx2≥－1；
因为b＞1，a≤2，对任意x∈[0，1]，可以推出
ax－bx2≤2x－bx2≤1，
即 ax－bx2≤1，
∴ －1≤f(x)≤1。
综上，当b＞1时，对任意x∈[0，1]，≤1的充要条件是b－1≤a≤。
（III）解：因为a＞0，0＜b≤1时，对任意x∈[0，1]；
f(x)= ax－bx2≥－b≥1，即f(x)≥－1；
f(x)≤1 Þ f(1)≤1Þ a－b≤1，即a≤b＋1，
a≤b＋1Þ f(x)≤(b＋1) x－bx2≤1，即f(x)≤1。
所以，当a＞0，1＜b≤1时，对任意x∈[0，1]，≤1的充要条件是a≤b＋1