高三12月教学质量调测数学试卷
(理科)
一.选择题(本大题共10小题,每小题5分,共50分)
1、设集合![]() 集合
集合![]() ,则P的个数是( )
,则P的个数是( )
A、6个 B、7个 C、8个 D、5个
2、![]() 是首项
是首项![]() ,公差
,公差![]() 的等差数列,如果
的等差数列,如果![]() ,则
,则![]() ( )
( )
A、500 B、501 C、502 D、503
3. ![]() 等于( )
等于( )
A、0 B、![]() C、
C、![]() D、
D、![]()
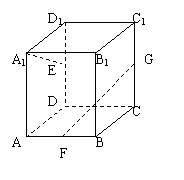 4、如图,长方体
4、如图,长方体![]() 中,
中,![]() ,点E、F、G分别是
,点E、F、G分别是![]() ,
,![]() 的中点,则异面直线
的中点,则异面直线![]() 与
与![]() 所成的角是( )
所成的角是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、如果函数![]() 的图象过点(2,1),那么
的图象过点(2,1),那么![]() 的图象一定过点( )
的图象一定过点( )
A、(1,2) B、(0,2) C、(1,1) D、![]()
6.条件p:![]() ,条件q:
,条件q:![]() ,则
,则![]() 成立的( )
成立的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.已知双曲线![]() 的两条渐近线的夹角为
的两条渐近线的夹角为![]() ,则双曲线的离心率为 ( )
,则双曲线的离心率为 ( )
A、![]() B、
B、![]() C、
C、![]() D、2
D、2
8.若![]() ,且
,且![]() ,则向量
,则向量![]() ( )
( )
A. ![]() B.
B.![]() C.
C. ![]() D.
D.![]()
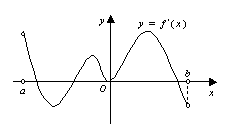 9.函数
9.函数![]() 的定义域为开区间
的定义域为开区间![]() ,导函数
,导函数![]() 在
在![]() 内的图象如图所示,则函数
内的图象如图所示,则函数![]() 在开区间
在开区间![]() 内有极小值点( )
内有极小值点( )
A.1个
B.2个
C.3个
D.4个
10.如果直线y=kx+1与圆![]() 交于M、N两点,且M、N关于直线x+y=0对称,则不等式组
交于M、N两点,且M、N关于直线x+y=0对称,则不等式组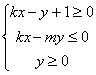 所表示的平面区域面积是( )
所表示的平面区域面积是( )
A.![]() B.
B.![]() C.1
D.2
C.1
D.2
二、填空题(本大题有4小题,每小题4分,共16分)
11.圆x2+y2=1上的点到直线3x+4y-25=0的距离的最小值为 。
12.定义运算![]() 的值域为
。
的值域为
。
13.已知f(x)是定义在实数集上的函数,且![]() ,则f(2006)= 。
,则f(2006)= 。
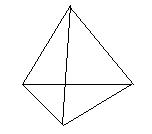 14.下面4个平面图形中,哪几个是右面正四面体的展开图?其序号是
。
14.下面4个平面图形中,哪几个是右面正四面体的展开图?其序号是
。
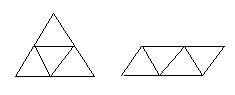
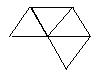
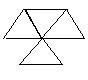
(1) (2) (3) (4)
三、解答题(本大题共6小题,每小题14分,共84分。解答应写出文字说明,证明过程或演算步骤)。
15.(本题满分14分)
已知![]() =
=![]() ,
,![]() =
=![]()
(1)若![]() +
+![]() =
=![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且
,且![]() ⊥
⊥![]() ,求
,求![]() 的值。
的值。
16.(本题满分14分)
设函数![]() .
.
(1)在区间![]() 上画出函数
上画出函数![]() 的图像;
的图像;
(2)设集合![]() . 试判断集合
. 试判断集合![]() 和
和![]() 之间的关系,并给出证明;
之间的关系,并给出证明;
17.(本题满分14分)
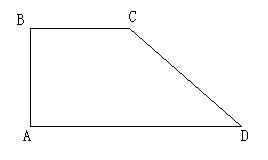
在梯形ABCD中,AB=BC=2,AD=4,∠CBA=∠BAD=90°,沿对角线AC将ΔABC折起,使点B在平面ACD内的射影O恰在AC上
(1)求证:AB⊥平面BCD;
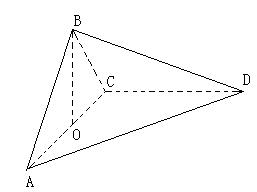 (2)求异面直线BC与AD所成的角。
(2)求异面直线BC与AD所成的角。
![]()
18.(本题满分14分)
已知函数f(x)=x3+ax2+bx+c在x=-![]() 与x=1时都取得极值
与x=1时都取得极值
(1) 求a、b的值与函数f(x)的单调区间
(2) 若对xÎ[-1,2],不等式f(x)<c2恒成立,求c的取值范围。
19.(本题满分14分)
已知函数![]() ,正数数列
,正数数列![]() 满足a1=1,
满足a1=1,![]() ,n∈N*,
,n∈N*,
(1)证明:an≤2;
(2)证明:an+1≥an;
(3)求![]() 的通项公式。
的通项公式。
20.(本题满分14分)
已知椭圆![]() 与直线x+y-1=0相交于两点A、B,椭圆的离心率为e
与直线x+y-1=0相交于两点A、B,椭圆的离心率为e
(1)
当椭圆的右准线方程为x=3,e=![]() 时,求AB的长度及AB中点的坐标;
时,求AB的长度及AB中点的坐标;
(2)
当![]() ,并且
,并且![]() (O为坐标原点)时,求椭圆长轴长的取值范围。
(O为坐标原点)时,求椭圆长轴长的取值范围。