高三（12）月测数学试卷

高三（12）月测数学试卷（文科）

命题：谭亚英　 审题：梁国铭

说明：考试时间为120分钟，满分150分。请把答案填在答题卷上，否则不给分。）

一、选择题（共10小题，每小题5分，共50分）

1、当1＜m＜3时，复数z=2＋m在复平面上对应的点位于（　　）

A、第一象限　　　　B、第二象限　　　　 C、第三象限　　　　D、第四象限

2、已知集合A=｛χN│－≤χ≤｝，则必有（　　）

A、-1A　　　　　 B、OA　　　　　　 C、A　　　　  D、2A

3、由a₁=1，d=3确定的等差数列｛｝，当=298时，序号n等于（　 ）

A、99　　　　　　  B、100　　　　　　  C、96　　　　　　  D、101

4、下列函数中周期是2的函数是（　　）

A、y=2cos²χ－1　　　　　　　　　 B、y=sin2χ＋cos2χ

C、y=tan()　　　　　　　　D、

5、条件甲：χ²＋y²≤4，条件乙：χ²＋y²≤2χ，那么甲是乙的（　　）

A、充分必要条件　　　　　　　  B、必要不充分条件

C、充要条件　　　　　　　　　  D、既不充分也不必要条件

6、△ABC中，D为BC的中点，已知=， =，则在下列向量中　　 与同向的向量是（　　）

A、  　　　　　　　　B、　

 C、　　　　　　　　　  D、

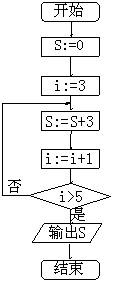
7、如右图所示的算法流程图中，输出S的值为（　 ）

A、3　　　　　  B、6　　 　　　 C、9　　　　　  D、12

8、直线：2χ＋by＋3=0过椭圆：10χ²＋y²=10的一个焦点，则b的值是（　　）

A、-1　　　　 B、　　　　 C、-1或1　　　　 D、-或

9、如右图，点P是球O的直径AB上的动点，PA=χ，过点P且与AB垂直的　　　 截面面积记为，则y=f (χ)的大致图象是（　 ）

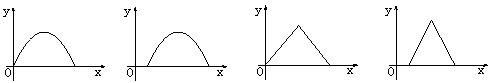
　　　A.　　　　　　　　 B.　　　　　　　  C.　　　　　　　  D.

10、对于R上可导的任意函数f (χ)，满足，则必有（　　）

A、f(0)＋f(2) ≥2 f (1)　　　　　　 B、f(0)＋f(2) ≤2 f (1)　

C、f(0)＋f(2) ＜2 f (1)　　　　　　 D、f(0)＋f(2) ＞2 f (1)　

二、填空题（每小题5分，共20分）

11、一个容量为20的样本，数据的分组与个组的频数如下：，2；, 3；, 4；, 5； , 4；,2；则样本在区间上的频率为　　　

12、已知函数f (χ)=  ，则f()－f(-) ＞的解集为　　　　 。

13、在△ABC中，a＋b=dc，且cotＣ=1003(cotA＋cotB)，则常数d的值等于　　　　 。

14、下列两题任选一题做：(注:若两小题都做,则按第(1)小题给分)

（1）正方体ABCD－ABCD中与对角线BD成为异面直线的棱线共有　　 条。

（2）椭圆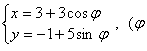是参数）的两个焦点坐标是　　　　　　  。

三、解答题（本大题共6小题，满分80分，解答应写出文字说明、证明过程或演算步骤）。

15、（12分）已知向量，向量

（1）若f()= ，且f ()的最小正周期为л，求f ()的最大值．

（2）在（1）的条件下，怎样由f ()的图象得到函数y=2sin2χ

16、（12分）已知三条直线：２χ－ y ＋a = 0（a＞0），直线：-4χ＋2y＋1=0和直线：χ＋y － 1 = 0 ，且与的距离是

（1）求a的值;

（2）求过与的交点且与两坐标轴截距相等的直线方程．

17、（14分）某地西红柿从2月1日起开始上市，通过市场调查，得到西红柿种植成本Q（单位：元/10）与上市时间（单位：天）的数据如下表：

时间	50	110	250
种植成本（元）	150	108	150

（1）根据上表数据，从下列函数中选取一个函数描述西红柿种植成本Q与上市时间的变化关系：

（2）利用你选取的函数，求西红柿种植成本最低时的上市天数及最低种植成本。

18、（14分）已知等比数列。

（1）求通项；

（2）若，数列的前n项的和为，且，求n的值。

19、（14分）设函数，其中R。

（1）若f (χ)在x=3处取得极值，求常数a的值；

（2）若f (χ)在（-，0）上为增函数，求a的取值范围．

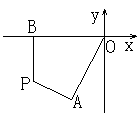20、（14分）如图，已知过原点O，从χ轴正方向出发逆时针旋转240°，得到射线，点A（χ, y）在射线上（χ＜0，y0）， 设｜│=2，又知点B（χ, y）在射线(χ＜0)上移动，设P为第三象限内的动点，若 且 ，，成等差数列.

（1）求P点的轨迹方程；

（2）已知点P的轨迹为C，直线的斜率为，若直线与曲线Ｃ有两个不同的交点M、N交线MN的中点为Q，求点Q的横坐标的取值范围。