高三（Ⅱ）圆锥曲线检测
一、选择题（本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的）
1．若椭圆经过原点,且焦点为
,则其离心率为 （ ）
A．
B．
C．
D．
2．下列方程的曲线关于x=y对称的是 （ ）
A．x2－x＋y2＝1 B．x2y＋xy2＝1
C．x－y=1 D．x2－y2＝1
3．若抛物线
的焦点与椭圆
的右焦点重合，则
的值为 （ ）
A．
B．
C．
D．
4．双曲线
的虚轴长是实轴长的2倍，则
（ ）
A．
B． C． D．
5．与
轴相切且和半圆
内切的动圆圆心的轨迹方程是 （ ）
A．
B．
C．
D． 
6．曲线
与曲线
的 （ ）
A．焦距相等 B．离心率相等 C．焦点相同 D．准线相同
7。 F1，F2是椭圆
( a>b.>0 ) 的两个焦点，过F1的弦AB与F2组成等腰直角三角形，其中∠BAF2=90°，则椭圆的离心率为
A 
B
C
D 
8．设过点
的直线分别与
轴的正半轴和轴的正半轴交于
、
两点，点
与点P关于轴对称，
为坐标原点，若
，且
，则
点的轨迹方程是 （ ）
A．
B．
C．
D．
9．抛物线
上的点到直线
距离的最小值是 （ ）
A．
B．
C．
D．
10．已知P是椭圆
上的点，Q、R分别是圆
和圆
上的点，则PQ+PR的最小值是 （ ）
A．
B．
C．10 D．9
11．已知抛物线
上一定点
和两动点
当
是,点的横坐标的取值范围是 （ ）
A．
B．
C．
D． 
12．椭圆
上有
个不同的点:
,椭圆的右焦点为
,数列
是公差大于
的等差数列,则的最大值为 （ ）
A．199 B．200 C．198 D．201
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中的横线上)
13．椭圆
的两个焦点为
,点在椭圆上.如果线段
的中点在轴上,那么
是
的______________倍.
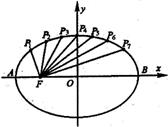
14．如图把椭圆
的长轴AB分成8等
分,过每个分点作x轴的垂线交椭圆的上半部
分于P1,P2,…,P7七个点,F是椭圆的焦点,则P1F+P2F+…+P7F= .
15．要建造一座跨度为16米,拱高为4米的抛物线拱桥,建桥时,每隔4米用一根柱支撑,两边的柱长应为____________.
16 已知m、n、m+n成等差数列，m、n、mn成等比数列，则椭圆
的离心率为————
高三（Ⅱ）圆锥曲线检测二卷
一选择题答案：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
二填空题
13—————— 14————— 15———— 16——————
三、解答题(本大题共6小题, 共74分,解答应写出文字说明,证明过程或演算步骤)
17 已知双曲线E的中心在原点，焦点在坐标系上，离心率e=
，且双曲线过点
P ( 2，
)求双曲线E的方程
18 椭圆 （ a>b>0 ）的两焦点为F1( 0
,-c ) ，F2 (
0, c ) ( c> 0 ) ，离心率e=
，焦点到椭圆上的点最短距离为2 -
。
(1)求椭圆的方程；
（2）设P 、Q为椭圆与直线y=x+1的两个交点，求tan∠POQ的值。
19 设双曲线：
的焦点为F!、F2，离心率为2。
（1）求双曲线渐近线L1、 L2的方程
（2）若A、B分别为L1、 L2上的得动点，且2AB=5 F!F2 ，求线段AB中点M的轨迹方程，并说明轨迹是什么曲线。
20 ）已知点
分别是椭圆
长轴的左、右端点,点是椭圆的右焦点.点在椭圆上,且位于轴的上方,
.
（1）求点的坐标;
（2）设
椭圆长轴
上的一点, 到直线
的距离等于
,求椭圆上的点到点的距离
的最小值.
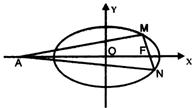
21．（14分）已知椭圆
的离心率为
，F为椭圆在x轴正半轴上的焦点，M、N两点在椭圆C上，且
，定点A（－4，0）.
（I）求证：当
时
；
（II）若当时有
，求椭圆C的方程；
（III）在（2）的条件下，当M、N两点在椭圆C运动时，试判断
是否有最大值，若存在求出最大值，并求出这时M、N两点所在直线方程，若不存在，给出理由.
