| 高三毕业班第一轮复习质量检测数学试卷 | 班级 姓名 学号 | |||||||||||
| 题号 | 一 | 二 | 三 | 总分 | |||||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||||
| 得分 | |||||||||||
考生注意：
1.答卷前,考生务必将班级、姓名、学号填写清楚.
2.本试卷共有
道试题,满分
分.考试时间
分钟.请考生用钢笔或圆珠笔将答案直接写在试卷上.
| 得分 | 评卷人 | 一、填空题(本大题满分 |
分)本大题共有
题,只要求直接填写结果,每个空格填对得1.有一密码为631208的手提式保险箱,现在显示的号码为080127 ,若要打开该保险箱,至少需要旋转 步(每个旋钮上转出一个新数字就为一步,逆转、顺转都可以).
2.我们用记号
来表示复数
,即
(其中
是自然对数的底数,单位是弧度),则
.
3.已知函数
的反函数
的图象过点
,则函数
的反函数的图象一定过点
.
4.在
中,角
、
、
所对边分别是
、
、
,且
,则的形状是
.
5.已知函数
,在其函数图象上,相邻的一个最大值点与一个最小值点恰好都在圆
上,则函数的最小正周期为
.
| 所购买的书的编号 | |
|
| 1,2,3,4,5 |
|
| 5,6,7,8,9 |
|
| 1,2,3,9,10 |
6.
、
、
、
位同学去购买编号分别为
的
种不同的书,为了节约经费和相互传阅方便,他们约定每人只购买其中
种不同的书各
本,且任意
位同学不能买全这种书,任意
位同学必须买全这种书.、、三位同学所购买的书的编号如右表所示,则同学买的书的号码应是
.
7.已知函数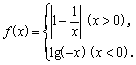
则关于
的方程
的解的个数是
.
8.已知函数是定义在实数集上的以为周期的奇函数,若
,
,则实数的取值范围是
.
9.已知数列
是由正数组成的数列,
且满足
,其中
且为整数,
,则
.
10.设点
、
为椭圆
的左、右焦点,过椭圆中心任作一直线与椭圆交于
、
两点,当四边形
面积最大时,
的值等于
.
11.定义
,其中
、
,且
.
若
,则
的值为
.
12.一水池有个进水口,个出水口,一个口进出水速度如图甲、乙所示.某天
点到
点,该水池的蓄水量如图丙所示(至少打开一个水口),给出以下个论断：
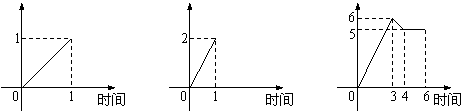进水量 出水量
蓄水量
甲 乙 丙
| ① | ② | ③ |
则一定不确定的论断是 (把你认为是符合题意的论断序号都填上).
| 得分 | 评卷人 | 二、选择题(本大题满分 |
分)本大题共有13.给出下列条件：
| ① | ② |
| ③ | ④ |
,
,
；
,
；
,
；
,
,且
.以上是
的充分不必要条件的个数是
| (A) | (B) | (C) | (D) |
[答]( )
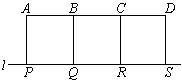14.如左图所示,、、、
是四个采矿点,
表示公路,线段表示道路,四边形
、
、
近似于正方形,、、、的采矿量之比为
,且运矿费用与路程、采矿量的乘积成正比,现在从、、
、
中选一中转站,使得采矿点到中转站费用最少,则应选
| (A) | (B) | (C) | (D) |
[答]( )
15.对于任意正整数
,定义的双阶乘
如下：
现在有如下四个命题：
反面还有试题
| ① | ② |
| ③ | ④ |
；
；
的个位数是
的个位数是其中正确的命题有
| (A) | (B) | (C) | (D) |
[答]( )
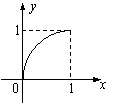16.已知定义在区间
上的函数
,图象如右图所示,对满足
的任意
、
,给出下列结论：
①
；
②
；
③
.
其中正确的结论有
| (A) | (B) | (C) | (D) |
[答]( )
三、解答题(本大题满分
分)本大题共有题,解答下列各题必须写出必要的步骤.
| 得分 | 评卷人 | 17.(本题满分 |
已知函数
(其中、为常数).
方程
有两个实根
,
.设
,
解关于的不等式
.
| 得分 | 评卷人 | 18.(本题满分 |
某山区的某种特产由于运输的原因,长期只能在当地销售,当地政府对该项特产的销售投资收益为：每投入万元,可获得利润
万元.当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为：在规划前后对该项目每年都投入
万元的销售投资,在未来年的前年中,每年都从万元中拨出
万元用于修建一条公路,年修成,通车前该特产只能在当地销售；公路通车后的年中,该特产既在本地销售,也在外地销售,在外地销售的投资收益为：每投入万元,可获得利润
万元.问从年的累积利润看,该规划方案是否可行？
| 得分 | 评卷人 | 19.(本题满分 |
分)本题共有
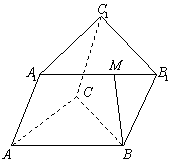
分.如图,三棱柱的底面是边长为的等边三角形,侧面
是
的菱形,且平面
平面
,
是棱
上的动点.
(1)当为棱的中点时,求证：
；
(2)试求二面角
的平面角最小时三棱锥
的体积.
| 得分 | 评卷人 | 20.(本题满分 |
设函数
(
,
).
(1)直线
能否为函数的图象的切线？若能,求出的值；若不能,请说明理由；
(2)若方程
有两个不等的实根、(重根只算一个根),不等式
对于
恒成立,求实数
的取值范围.
反面还有试题
| 得分 | 评卷人 | 21.(本题满分 |
自然状态下的鱼类是一种可再生的资源.为持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响.用
表示某鱼群在第年年初的总量,,且
.不考虑其他因素,设在第年内鱼群的繁殖量及被捕捞量都与成正比,死亡量与
成正比,这些比例系数依次为正常数、、.
(1)求
与的关系式；
(2)猜测：当且仅当、、、满足什么条件时,每年年初鱼群的总量保持不变(不要求证明,但要有猜测过程)？
(3)设
,
,为保证对任意
,都有
(),则捕捞强度的最大允许值是多少？证明你的结论.
| 得分 | 评卷人 | 22.(本题满分 |
分)本题共有
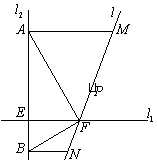如图所示,
且
,
且
(),过
点的任意直线(不与
重合)交曲线于、
两点,
为
的角平分线,
(、
),
,为线段
的中点.
(1)建立适当的直角坐标系,求曲线的方程；
(2)若
,证明：
；
(3)若是奇素数(素数是指只能被和它自身整除的正整数),且点到直线、
的距离均为非零整数,证明：到
中点的距离不是整数.