高三第二次大考数学试卷

高三第二次大考数学试卷

一　选择题：本大题共12小题，每小题5分，共60分　

1、已知集合P={(x，y)x+y=1}，Q={(x，y)x²+y²≤1}，则【A】

（A）PQ　　　　　 （B）P=Q　　　　　 （C）PQ　　　　  （D）P∩Q=Q

2、双曲线渐近线l方程为，则双曲线焦点F到渐近线l的距离为【 C　】　　　　　　　　　　　　　 

　　　 （A）2　　　　　　　　　　 （B）　　　　　　　 （C）　　　　　　　　（D）2

3、如果函数的反函数是，则下列等式中正确的是【 B 】　　　　　　　　　 

（A）　　　　　　　　　　　　（B）

（C）　　　　　　　 　　（D）

4、设向量的模等于4, 与的夹角为，则在方向上的投影为【 B 】

（A） 2　　　　 （B） -2　　 （C） 2　　　　　　　（D） -2

5、【理】直线与曲线有公共点，则的取值范围是【 D　】

　　（A）　　　　（B）　　　　　　（C）　　　　（D）

【文】已知两点A（3，2）和B（－1，4）到直线距离相等，则m值为【　D 】

　　　 （A）　　　　 （B）　　　　　　（C）　　　　　（D）

6、已知长方形的四个顶点A(0，0)，B(2，0)，C(2，1)和D(0，1)．一质点从AB的中点沿与AB夹角为θ的方向射到BC上的点后，依次反射到CD、DA和AB上的点和（入射角等于反射角)．设的坐标为若，则tanθ的取值范围是【 C 】

　　　　 　　　　　　　　　　　　　　

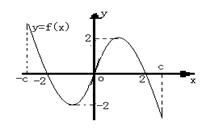7、是定义在区间[-c，c]上的奇函数，其图象如图所示：令,则下列关于函数的叙述正确的是【　B  】

（A）若，则函数的图象关于原点对称

（B）若，则方程有大于2的实根

（C）若，则方程有两个实根

（D），则方程有三个实根

8、设函数的图象上的点的切线的斜率为，若，则函数的图象大致为【 A　】

（A）　　　　　　　　　　　　　（B）　　　　　　　　　　 （C）　　　　　　　　　　（D）

9、△ABC边上的高线为AD，BD=a，CD=b，且a＜b，将△ABC沿AD折成大小为的二面角

B—AD—C。若cos=，则三棱锥A—BDC的侧面△ABC是【C】

（A）锐角三角形  （B）钝角三角形 （C）直角三角形 （D）形状与a、b的值有关的三角形

10、对2×2数表定义平方运算如下：

　。 则的值为【 C　】

（A）　　（B）　　  （C） 　　　（D）

11、平面直角坐标系中，为坐标原点，已知两点（2，－1），（－1，3），若点满足其中0≤≤1，且，则点的轨迹方程为【　C 】

　　（A）　　　　　　　　　　　　　 （B）　　　　　　 

　　（C）（－1≤≤2）　　　　　　 （D）（－1≤≤2）

12、已知是三角形的一个内角，且，则方程表示 【 B　】

　　（A）焦点在轴上的椭圆　　　　　　　  （B）焦点在轴上的椭圆　　

　　（C）焦点在轴上的双曲线　　　　　　  （D）焦点在轴上的双曲线

二　填空题：

13 【理】找一个非零函数，使，则的解析式可以是_________；

【文】在(x²+－4)⁵的展开式中含x⁴项的系数是___________；

14　某公司生产三种型号的轿车，产量分别为1 200辆，6 000辆和2 000辆．为检验该公司的产品质量，现用分层抽样方法抽取46辆进行检验，这三种型号的轿车依次应抽取____________，_______________，____________辆；

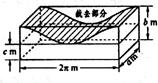
15．一块长方体木料，按图中所示的余弦线截去一块，

则剩余部分的体积是　　　　　　　　 ；

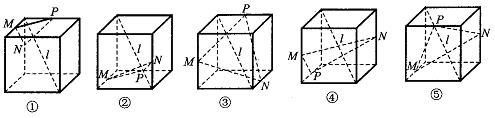
16．下列5个正方体图形中，是正方体的一条对角线，点M、N、P分别为其所在棱的中点，能得出⊥面MNP的图形的序号是_______。(写出所有符合要求的图形序号)

三　解答题(共6小题)

17、 【理】A　B　C为△ABC的三内角，且其对边分别为a　b　c

若 , ，且·＝　　

（1）求角A的大小；　 （2）若a＝2，三角形面积S＝，求b+c的值　

【文】解关于x的不等式：，（a＞0且a≠1）．

18．有外形相同的球分装在三个不同的盒子中，每个盒子10个球，其中第一个盒子中7个球标有字母A，3个球标有字母B；第二个盒子中有红球和白球各5个；第三个盒子中有红球8个，白球2个，试验按如下规则进行：先在第一个盒子中任取一球，若取得标有字母A的球，则在第二个盒子中任取一球；若第一次取得标有字母B的球，则在第三个盒子中任取一球。如果第二次取出的是红球，则称试验成功，求试验成功的概率

19、已知函数f(x)=－x³＋3x²＋ax＋b在x＝(1，f(1))处的切线与直线12x－y－1＝0平行．

（1）求实数a的值；

（2）求f(x)的单调递减区间；

（3）若f(x)在区间[－2，2]上的最大值为20，求它在该区间上的最小值．

　

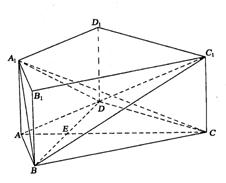20、如图, 在直四棱柱ABCD－A₁B₁C₁D₁中，AB＝AD＝2，

DC＝2，AA₁＝，AD⊥DC，AC⊥BD, 垂足为E，

　（I）求证：BD⊥A₁C；

　（II）求二面角A ₁－BD－C ₁的大小；

　（III）求异面直线 AD与 BC ₁所成角的大小．

21、【理】已知中心在原点的椭圆C焦点在x轴上，一条经过点（3，－）且方向向量为的直线l交椭圆C于A、 B两点，交x轴于M点，又　

　　　 （1）求直线l方程；　（2）求椭圆C长轴长取值的范围　

【文】已知中心在原点的椭圆C的左焦点为，右顶点为（2，0）．

（1）求椭圆C的方程；

（2）若直线与椭圆C有两个不同的交点A和B，且（其中O为原点）, 求实数m的取值范围.

22．（本小题满分14分）

已知数列的首项=4，前n项和为S_n ，且

（1）求数列的通项公式；

（2）设函数=

南康二中高三数学周练试卷（七）参考答案

一　选择题ACBBD CBACC　 CB

6、解法1  取特殊的θ角，当时，根据反射原理，得点依次是BC，CD，DA和AB的中点，即有不属于所求的tanθ的取值范围．从而，可排除选项A、B和D，应取C作答．

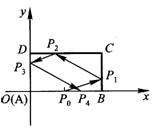
解法2　依题设可作图如下．记各点的坐标如下：

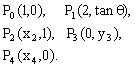
根据反射原理得：

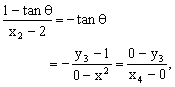
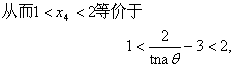
二　填空题

13、【理】【文】－960 ；14 、 6，30，10

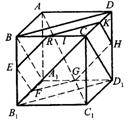15、　a(b+c)πm³　；16、①④⑤ 【提示】作正方体ABCD-A₁B₁C₁D₁如图，与题设图形对比讨论．在下图中，三个截面BA₁D、EFGHKR和C₁B₁D都是对角线（即AC的垂面．

对比图①，由MP∥BD,，故得⊥面MNP．

对比图②，由MN与面相交，而过交点且与垂直的直线都应在面内，

所以MN不垂直于，从而不垂直于面MNP．

对比图③，由MP与面相交，知不垂直于MN，故不垂直于面MNP．

对比图④，由MN∥BD，故⊥面MNP．

对比图⑤，面MNP与面EFGHKR重合，故⊥面MNP．

三　解答题

17【理】解：（1）∵，，且·＝，

∴－cos²＋sin²＝， 即－cosA＝，又A∈(0，p)，∴A＝p……6分

　 　　　　（2）S_△ABC＝bc·sinA＝b·c·sinp＝，∴bc＝4, 

又由余弦定理得：a²=b²+c²－2bc·cos120°＝b²+c²+bc ,∴16＝(b+c)²，故b+c＝4 …………12分

【文】解：…………………………………………（6分）

　　　　   …………………………………………………（8分）

　　　　  当0＜a＜1时，a²＜a，不等式解集为{} ………（10分）

　　 当a＞1时，不等式解集为 ……………………（12分）

18、解：设事件A{从第一个盒子中取得一个标有字母A的球}，事件B={从第一个盒子中取得一个标有字母B的球}，则A，B互斥，且P（A）=，P（B）=；（4分）

事件C={从第二号盒子中取一个红球}，事件D={从第三号盒子中取一个红球}，

则C，D互斥，且P（C）=（8分）显然，事件A·C与事件B·D互斥，且事件A与C是相互独立的， B与D也是相互独立的.所以试验成功的概率为

（11分）

答：本次试验成功的概率为

19、解：（1） ∵f ’(x)＝－3x²＋6x＋a 　　　　

∴f ’(1)＝3＋a=12,∴a=9　 　　　　　　　 

（2） f ’(x)＝－3x²＋6x＋9．

令f ‘(x)<0，解得x<－1或x>3，　　　　

所以函数f(x)的单调递减区间为（－∞，－1），（3，＋∞）．

（3）因为f(－2)＝8＋12－18＋b=2＋b，

f(2)＝－8＋12＋18＋b＝22＋b，

所以f(2)>f(－2)．　　　　　　　　　　　　　

因为在（－1，3）上f ‘(x)>0，

所以f(x)在[－1, 2]上单调递增，又由于f(x)在[－2，－1]上单调递减，

因此f(2)和f(－1)分别是f(x)在区间[－2，2]上的最大值和最小值，

于是有 22＋b＝20，解得 b＝－2．　 　　 

故f(x)=－x³＋3x²＋9x－2，因此f(－1)＝1＋3－9－2＝－7，

即函数f(x)在区间[－2，2]上的最小值为－7．

20、（I）在直四棱柱ABCD－AB₁C₁D₁中，

∵AA₁⊥底面ABCD．∴ AC是A₁C在平面ABCD上的射影．

　 ∵BD⊥AC．∴ BD⊥A₁C；

（II）连结A₁E，C₁E，A₁ C₁．

　 与（I）同理可证BD⊥A₁E，BD⊥C₁E，

∴ ∠A₁EC₁为二面角A₁－BD－C₁的平面角．　∵　AD⊥DC，∴ ∠A₁D₁C₁=∠ADC＝90°，

　　又A₁D₁=AD＝2，D₁C₁= DC＝2，AA₁=且 AC⊥BD，

　　∴ A₁C₁＝4，AE＝1，EC＝3，∴ A₁E＝2，C₁E＝2，

　　在△A₁EC₁中，A₁C₁²＝A₁E²＋C₁E²，　∴ ∠A₁EC₁＝90°，

　　即二面角A₁－BD－C₁的大小为90°．

（III）过B作 BF//AD交 AC于 F，连结FC₁，

　　则∠C₁BF就是AD与BC₁所成的角． ∵　AB＝AD＝2， BD⊥AC，AE＝1，　∴ BF=2，EF＝1，FC＝2，BC＝DC，∴ FC₁=，BC₁＝，

　　在△BFC₁ 中，,∴ ∠C₁BF=

　　即异面直线AD与BC₁所成角的大小为．

21、【理】解：（1）直线l过点（3，－）且方向向量为

　　　 化简为：

　　　 （2）设直线交于两点A（x₁,y₁），B（x₂,y₂），和x轴交于M（1，0）由

　　　 将…①

………………② ………………③

　　　 由韦达定理知：

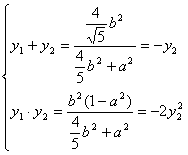
由②²/③ 知：32b²=（4b²+5a²）（a²－1）

　　　 化为…………④

　　　 对方程①求判别式，且由△>0

　　　 即

　　　 化简为：…………⑤

　　　 由④式代入⑤可知：又椭圆的焦点在x轴上，

　　则由④知：

　　　

　　　 因此所求椭圆长轴长2a范围为（

【文】解：（Ⅰ）设椭圆方程为　

由已知得

故椭圆C的方程为　　　　　　 …………………………………4’

（Ⅱ）将 　　　

由直线l与椭圆C交于不同的两点得

即　　　　　　　　　　　　　　　 …………………………………8’

①  设，则

　　　 …………………………………10’

而

于是 即　　②　　 …………………………………12’

由①、②得　

故m的取值范围为

22解：① ≥　 ①

≥　　②

①—②得≥　　　　　　　　　　　　　  （2分）

又　

≥　　　　　　　　　　　　　　　　　　 （4分）

 为等比数列

　　　　　　　　　　　　　　　　　　　　　　　　 （6分）

②

 

　　　　　　　　　　　　　 （12分）

　　　　　　　　　　　　　　　 （14分）