高三第二次调研考试预演题

高三第二次调研考试预演题

注意事项：

1.本试卷分为第一卷(试题卷)和第二卷(答题卷)两部分,满分150分.考试时间120分钟.

2.请将第一卷的答案填涂在第二卷指定的位置

一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.

1.已知是两个非零向量,则不共线是<的——————————(　 )

A.充分不必要条件　 B.必要不充分条件　 C.充要条件　　 D.即不充分也不必要条件

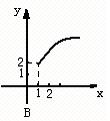
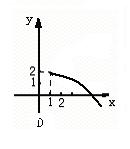
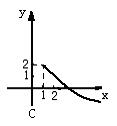
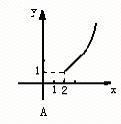2.函数y=x²-4x+5(x≤2)的反函数的图象大致是—————————————————(　 )

3.甲、乙、丙、丁、戊5名学生进行比赛，决出了1到5的名次. 甲、乙向评委询问成绩, 评委对甲说:“你和乙都未拿到冠军”,对乙说:“你不是最差的”.由此分析,5人名次排列的可能情况共有—————————————————————————————————(　 )

A.36种　　　　　　　B.48种　　　　　 　　 `　C.54种　　　　　　　  D.72种

4.若直线2ax-by+2=0(a>0,b>0)被圆截得的弦长为4,则的最小值是——————————————————————————————————(　 )

A.　　　　　　　  B.　　　 　　　　　 C.2　　　　　　　　　  D.4

5.若α、β 是两个不同的平面，m、n是两条不同的直线，则下列命题中不正确的是（　 ）

A.α∥β,m⊥α则m ⊥β 　　　　B.n∥α, n⊥β则α⊥β　

C. m ∥n , m⊥α则n⊥α　　　　　D.α∩β=m,n与α,β所成的角相等,则m⊥n

6.已知等差数列前n项和为,且,则过点和

()的直线的一个方向向量的坐标可以是————————————————（　 ）

A.　　　　　 B.　　　　　 C.　　　　  D.

7.若关于方程在上有解,则实数m的取值范围是———————(　 )

A.　　　　　 B.　　　　　　　　 C.　　　　D.

8.已知向量,,若y=x+则向量的夹角为(　 )

A.　　　　　　  B.　　　　　　　　　  C.　　　　　　　 D.

9.已知函数,则的值为————————————(　 )

A.　　　　　　  B.　　　　　　　　  C.4　　　　　　　  D.8

10.设函数的定义域为D,如果对于任意的,存在唯一的,使(c为常数)成立,则称函数在D上均值为c,给出下列四个函数:①②③④则满足在定义域上均值为2的所有函数是—(　 )　

A.①②　　　　　　　  B.③④　　　　　　　　  C.②④　　　　　　 D.①③

二、填空题（本大题共6小题，每小题5分，共30分）

11.设周期为4的奇函数f(x)的定义域为R且当x∈[4，6 )时，f(x)=2-x²则f(-1)的值为_________

12.设(x-1)ⁿ=a₀+a₁x+a₂x²+……+a_nxⁿ(n≥3且n∈Z)若a₃+3a₂=0,则n的值为____________.

13.对共有10人的一个数学小组做一次数学测验，测试题由10道单项选择题构成，每答对1题得5分，答错或不答得0分，批阅后的统计得分情况如下：

得分	50分	≥45分	≥40分	≥35分
人数	2	4	8	10

则这次测试平均成绩为_____________________.

14．已知则的最小值为_________________.

15.把实数a,b,c,d排列成形如的形式,称之为二行二列矩阵,定义矩阵的一种运算,,该运算的几何意义为平面上的点在矩阵的作用下变换成点,则点在矩阵的作用下变换成点____________,

又若曲线在矩阵的作用下变换成曲线,则a+b的值为_______________.

16.将正方形ABCD沿对角线BD折成直二面角后，有下列四个结论：①AC⊥BD②△ACD是等边三角形③AB与平面BCD所成的角为60⁰④AB与CD所成的角为60⁰

其中正确结论的序号为^{_____________________________________.}

三:解答题(本大题共5小题,共70分.解答时应写出文字说明、证明过程或演算步骤) 　 

 17. (本小题满分12分)黄种人群中血型的人所占的比如下表所示

血型	A	B	AB	O
该血型的人所占的百分比	28	29	8	35

已知同种血型的人可以输血，O型血可以输给任一种血型的人，任何人的血可以输给AB型的人，其他不同血型的人不能互相输血，小明是B型血，若小明需要输血，问:

（1）　　　 任找一个人，其血可以输给小明的人的概率是多少？

（2）　　　 任找两个人，当中至少有一个人，其血可以输给小明的概率是多少？

18. (本小题满分14分)已知双曲线C₁的方程为椭圆的长轴的两个端点恰好为双曲线的两个焦点

（1）如果椭圆的两个焦点又是双曲线的两个顶点，求椭圆的方程

（2）如果椭圆的方程为且椭圆上存在两点A、B关于直线 y=x-1对称,

求b的取值范围

19.(本小题满分14分)已知函数f(x)=ax³+3x²-6ax-11,g(x)=3x²+6x+12和直线m:y=kx+9,又

（1）求a的值

（2）是否存在k的值，使直线m既是曲线y=f(x)的切线，又是y=g(x)的切线，如果存在，求出k的值，若不存在，说明理由

（3）如果对所有x≥-2的x，都有f(x)≤kx+9≤g(x)成立,求k的取值范围

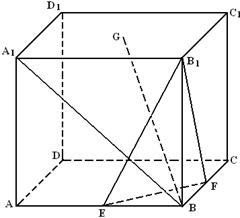20.(本小题满分14分) 如图,在棱长为a 的正方体中,E,F分别是棱AB和BC的中点,G为上底面的中心.

⑴求AD与BG所成的角的余弦值;

⑵求二面角B-FB₁-E的大小;

⑶求点D到平面B₁EF的距离.

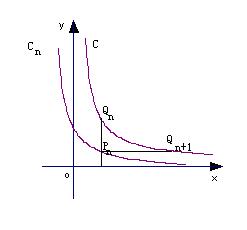21.(本小题满分16分)已知曲线C：，从C上的点作x轴的垂线，交于点，再从点作y轴的垂线，交C于点，设，.

（1）　　　 求的坐标；

（2）　　　 求数列的通项公式；

（3）　　　 记数列的前n项和为，求证：。

．