高考数学普通高等学校招生全国统一考试128
一．选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个备选项中，只有一项是符合题目要求的。
（1）已知集合
，
，
，则
（A）
（B）
（C）
（D）
（2）在等差数列
中，若
且
，
的值为
（A）2 （B）4 （C）6 （D）8
（3）以点（2，－1）为圆心且与直线
相切的圆的方程为
（A）
（B）
（C）
（D）
（4）若
是平面
外一点，则下列命题正确的是
（A）过只能作一条直线与平面相交 （B）过可作无数条直线与平面垂直
（C）过只能作一条直线与平面平行 （D）过可作无数条直线与平面平行
（5）
的展开式中
的系数为
（A）－2160 （B）－1080 （C）1080 （D）2160
（6）设函数
的反函数为
，且
的图像过点
，则的图像必过
（A） （B）
（C）
（D）
（7）某地区有300家商店，其中大型商店有30家，中型商店有75家，小型商店有195家。为了掌握各商店的营业情况，要从中抽取一个容量为20的样本。若采用分层抽样的方法，抽取的中型商店数是
（A）2 （B）3 （C）5 （D）13
（8）已知三点
，其中
为常数。若
，则
与
的夹角为
（A）
（B）
或
（C）
（D）或
（9）高三（一）班学要安排毕业晚会的4各音乐节目，2个舞蹈节目和1个曲艺节目的演出顺序，要求两个舞蹈节目不连排，则不同排法的种数是
（A）1800 （B）3600 （C）4320 （D）5040
（10）若
，
,
，则
的值等于
（A）
（B）
（C）
（D）
（11）设
是右焦点为
的椭圆
上三个不同的点，则“
成等差数列”是“
”的
（A）充要条件 （B）必要不充分条件
（C）充分不必要条件 （D）既非充分也非必要
（12）若
且
，则
的最小值是
（A）
（B）3 （C）2 （D）
二．填空题：本大题共4小题，每小题4分，共24分。把答案填写在答题卡相应位置上。
（13）已知
，
，则
。
（14）在数列
中，若
，
，则该数列的通项
。
（15）设
，函数
有最小值，则不等式
的解集为
。
（16）已知变量
，
满足约束条件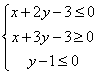
。若目标函数
（其中
）仅在点
处取得最大值，则
的取值范围为
。
三．解答题：本大题共6小题，共76分。解答应写出文字说明、证明过程或演算步骤。
（17）（本小题满分13分）
甲、乙、丙三人在同一办公室工作。办公室只有一部电话机，设经过该机打进的电话是打给甲、乙、丙的概率依次为
、
、。若在一段时间内打进三个电话，且各个电话相互独立。求：
（Ⅰ）这三个电话是打给同一个人的概率；
（Ⅱ）这三个电话中恰有两个是打给甲的概率；
（18）（本小题满分13分）
设函数
（其中
）。且
的图像在轴右侧的第一个最高点的横坐标是
。
（Ⅰ）求
的值；
（Ⅱ）如果在区间
上的最小值为，求的值；
（19）（本小题满分12分）
设函数
的图像与直线
相切于点
。
（Ⅰ）求
的值；
（Ⅱ）讨论函数的单调性。
（20）（本小题满分12分）
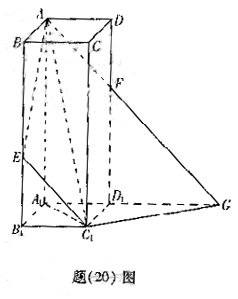如图，在增四棱柱
中，
，
为
上使
的点。平面
交
于，交
的延长线于
，求：
（Ⅰ）异面直线
与
所成角的大小；
（Ⅱ）二面角
的正切值；
（21）（本小题满分12分）
已知定义域为
的函数
是奇函数。
（Ⅰ）求的值；
（Ⅱ）若对任意的
，不等式
恒成立，求的取值范围；
（22）（本小题满分12分）
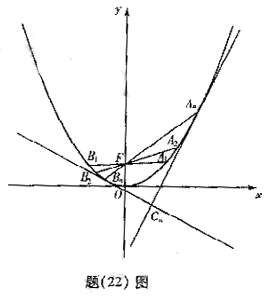如图，对每个正整数
，
是抛物线
上的点，过焦点的直线
角抛物线于另一点
。
（Ⅰ）试证：
；
（Ⅱ）取
，并记
为抛物线上分别以
与
为切点的两条切线的交点。试证：
；
普通高等学校招生全国统一考试参考答案
一．选择题：DDCDB CCDBB AA
二．填空题：（13）-2 （14）
（15）
（16）
三．解答题：满分74分
（17）解：（Ⅰ）由互斥时间有一个发生的概率公式和独立事件同时发生的概率公式，所求概率为
（Ⅱ）这是 
，
的独立重复实验，故所求概率为
（18）解：（Ⅰ）
依题意得 
， 解得 
（Ⅱ）由（Ⅰ）知，
又当
时，
，故
，
从而在上取得最小值
.
因此，由题设知
.故
.
（19）解：（Ⅰ）求导得
.
由于的图象与直线相切与点，
所以
，
，即
解得
，
.
（Ⅱ）由，得
.
令
，解得
或
；又令
，解得
.
所以当
时，是增函数；当
时，也是增函数；但
时，是减函数.
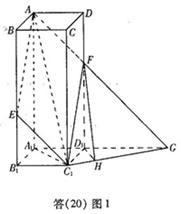（20）解法一：（Ⅰ）由
知
为异面直线与所成的角.连接
.因为
和分别是平行平面
和
与平面
的交线，所以
，由此可得
.再由
得
.
在
中，由
，得
。
（Ⅱ）作
于
，连接
。由三垂线定理知
，故
为二面角
即二面角的平面角。
在
中，由，
得
。
从而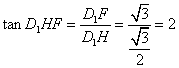
.
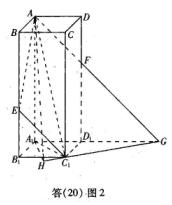解法二：（Ⅰ）由知为异面直线与所成的角。
因为
和
是平行平面
与
与平面的交线，
所以
. 由此可得
,
从而
，于是。
在中，由，得。
（Ⅱ）在
中，由
，
知
为钝角。作
交
的延长线于，连接
。由三垂线定理知
，故
为二面角的平面角。
在
中，由
，
得
。
从而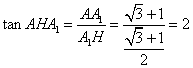
。
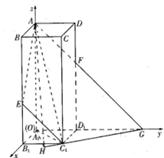解法三： （Ⅰ）以A1为原点，A1B1，A1D1，A1A所在直线分别为x轴，y轴和z轴建立如图所示的空间直角坐标系.于是，
因为EC1和AF分别是平行平面 BB1C1C和AA1D1D与平面AEC1G的交线，
所以EC1//AF.设G（0, y, 0），则
.
由
得
，于是
。
故
.
设异面直线AD与C1G所成的角的大小为
，则
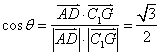,从而 
。
（II）作
于H，由三垂线定理知
,故为二面角的平面角。设
，则
，
。
由得
，由此得
。 ①
又由H,C1,G共线得
，从而
，于是
②
联立1和2得
。
由
, 
得
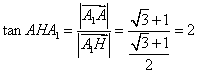
（21）解：（Ⅰ）因为是奇函数，所以
，即
，解得
。
从而有
， 又由
知
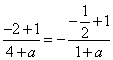，解得
。
（Ⅱ）解法一： 由（Ⅰ）知
由上式易知在
上为减函数。
又因是奇函数，从而不等式
等价于
因是减函数，由上式推得
即对一切有
从而判断别式
，解得
解法二：由（Ⅰ）知
,又由题设条件得
即 
整理得 
,因底数
,故
上式对一切均成立,从而判别式,解得
(22)证明：(Ⅰ)对任意固定的
,因为焦点
,所以可设直线
的方程为
,将它与抛物线方程联立得
,
由一元二次方程根与系数的关系得
（Ⅱ）对任意固定的，利用导数知识易得抛物线在处的切线的斜率
，
故在处的切线方程为
， ①
类似地，可求得在处的切线方程为 
， ②
由②减去①得 
，
从而
， 
，
， ③
将③代入①并注意得交点的坐标为
.
由两点间的距离公式得
=
.
从而
.
现在
，利用上述已证结论并由等比数列求和公式得，
…
…
=
.