高考数学普通高等学校招生全国统一考试
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ⅰ卷1至2页。第Ⅱ卷3至8页。共150分。考试时间120分钟。
第Ⅰ卷（选择题共60分）
注意事项：
1．答第Ⅰ卷前，考生务必将自己的姓名、考生号、座位号、考试科目、试卷类型（A或B）用铅笔涂写在答题卡上，同时将才生号条形码粘贴在答题卡“条形码粘贴处”。
2．每小题选出答案后，用铅笑把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。
3．考试结束，监考人将本试卷和答题卡一并收回。
参考公式：
三角函数的积化和差公式
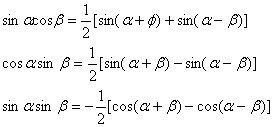
正棱台、圆台的侧面积公式
其中
、
分别表示上、下底面周长，
表示斜高或母线长
台体的体积公式
其中
、
分别表示上、下底面积，
表示高。
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。
（1）已知集合
，那么
的真子集的个数是：
（A）15 （B）16 （C）3 （D）4
（2）在复平面内，把复数
对应的向量按顺时钟方向旋转
，所得向量对应的复数是：
（A）2
（B）
（C）
（D）3+
（3）一个长方体共一顶点的三个面的面积分别是
，，
，这个长方体对角线的长是：
（A）2
（B）3
（C）6 （D）
（4）已知
＞
，那么下列命题成立的是
（A）若、是第一象限角，则
＞
（B）若、是第二象限角，则
＞
（C）若、是第三象限角，则＞
（D）若、是第四象限角，则＞
（5）函数
的部分图象是
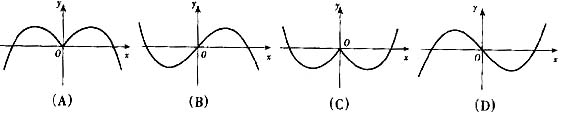
（6）《中华人民共和国个人所得税法》规定，公民全月工资、薪金所得不超过800元的部分不必纳税，超过800元的部分为全月应纳税所得额，此项税款按下表分段累进计算：
| 全月应纳税所得额 | 税率 |
| 不超过500元的部分 | 5% |
| 超过500元至2000元的部分 | 10% |
| 超过2000元至5000元的部分 | 15% |
| … | … |
某人一月份应交纳此项税款26.78元，则他的当月工资、薪金所得介于
（A）800~900元 （B）900~1200元 （C）1200~1500元 （D）1500~2800元
（7）若
＞
＞1，
，则
（A）R＜P＜Q （B）P＜Q＜R （C）Q＜P＜R （D）P＜R＜Q
（8）以极坐标系中的点（1，1）为圆心，1为半径的圆的方程是
（A）
（B）
（C）
（C）
（9）一个圆柱的侧面展开图是一个正方形，这个圆柱的全面积与侧面积的比是
（A）
（B）
（C）
（D）
（10）过原点的直线与圆
+
+
+3=0相切，若切点在第三象限，则该直线的方程是
（A）
（B）
（C）
（D）
（11）过抛物线
的焦点F作一直线交抛物线于P、Q两点，若线段PF与FQ的长分别是p、q，则
+
等于
（A）
（B）
（C）
（D）
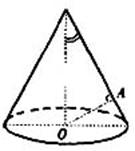（12）如图，
是圆雏底面中心
互母线的垂线，绕轴旋转一周所得曲面将圆锥分成体积相等的两部分，则母线与轴的夹角的余弦值为
（A）
（B）
（C）
（D）
第Ⅱ卷（非选择题共90分）
注意事项：
1．第Ⅱ卷共6页，用钢笔或圆珠笔直接答在试题卷中。
2．答卷前将密封线内的项目填写清楚，并在试卷右上角填上座位号。
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。
（13）乒乓球队的10名队员中有3名主力队员，派5名参加比赛，3名主力队员要安排在第一、三、五位置，其余7名队员选2名安排在第二、四位置，那么不同的出场安排共有 种（用数字作答）。
（14）椭圆
的焦点
、
，点
为其上的动点，当∠为钝角时,点 横坐标的取值范围是
。
（15）设
是首项为1的正项数列，且（n+1）
(n=1，2，3，…)，则它的通项公式是
。
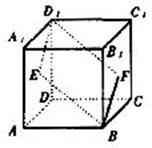
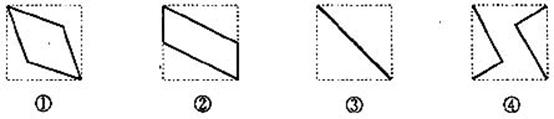
（16）如图，E、F分别为正方体面ADD1A1、面BCC1B1的中心，则
四边形BFD1E在该正方体的面上的射影可能
是 。
（要求：把可能的图序号都填上）
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤。
（17）（本小题满分12分）
已知函数
（Ⅰ）当函数
取得最大值时，求自变量
的集合；
（Ⅱ）该函数的图象可由
的图象经过怎样的平移和伸缩变换得到？
（18）（本小题满分12分）
设
为等比数例，
，已知
，
。
（Ⅰ）求数列的首项和公式；
（Ⅱ）求数列
的通项公式。
（19）（本小题满分12分）
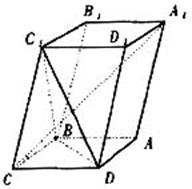如图，已知平行六面体ABCD—A1B1C1D1的底面ABCD上菱形，且∠C1CB=∠C1CD=∠BCD，
（Ⅰ）证明：C1C⊥BD；
（Ⅱ）当
的值为多少时，能使A1C⊥平面C1BD？请给出证明。
（20）（本小题满分12分）
设函数
，其中
。
（Ⅰ）解不等式
≤1；
（Ⅱ）证明：当≥1时，函数在区间[0，+∞]上是单调函数。
（21）（本小题满分12分）
某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿场售价与上市时间的关系用图一的一条折线表示；西红柿的种植成本与上市时间的关系用图二的抛物线段表示。
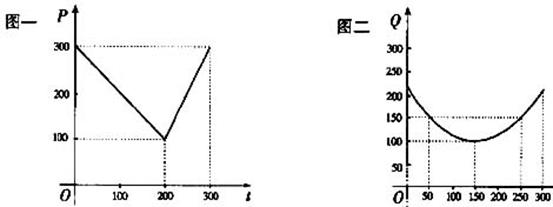
（Ⅰ）写出图一表示的市场售价与时间的函数关系式
；
写出图二表示的种植成本与时间的函数关系式
；
（Ⅱ）认定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大？
（注：市场售价各种植成本的单位：元/102㎏，时间单位：天）
（22）（本小题满分14分）
如图，已知梯形ABCD中AB=2CD，点E分有向线段
所成的比为
，双曲线过C、D、E三点，且以A、B为伪点，当
时，求双曲线离心率c的取值范围。
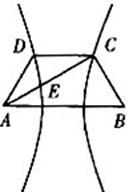
普通高等学校招生全国统一考试数学试题参考答案
说明：
一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不局，可根据试题的主要考查内容比照评分标准制订相应的评分细则。
二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分。
三、解答右端所注分数，表示考生正确做到这一步应得的累加分数。
四、只给整数分数，选择题和填空不给中间分。
一、选择题：本题考查基本知识和基本运算，每小题5分，满分60分。
（1）A （2）B （3）D （4）D （5）D
（6）C （7）B （8）C （9）A
（10）C （11）C （12）D
二、填空题：本题考查基本知识和基本运算，每小题4分，满分16分。
（13）252 （14）
（15）
（16）23
三、解答题
（17）本小题主要考查三角函数的图象和性质、利用三角公式进行恒等变形的技能以及运算能力。满分12分。
解：（1）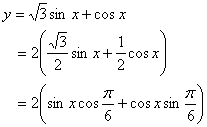
。
…………3分
取得最大值必须且只需
即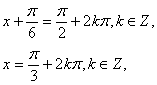
所以，使函数取得最大值的自变量的集合为
…………6分
（Ⅱ）变换的步骤是：
（1）把函数
的图象向左平移
得到
…………9分
的图象；
（2）令所得到的图象上各点横坐标不变，把纵坐标伸长到原来的2倍，得到
的图象；
经过这样的变换就得到函数
的图象。
…………12分
（18）本小题主要考查等比数列的基础知识和基本技能，运算能力，满分12分。
（Ⅰ）解：设等比数列以比为
，则
。
…………2分
∵
，
∴
。
…………4分
（Ⅱ）解法一：由（Ⅰ）知，故
,
因此，
，
…………6分
∴
。
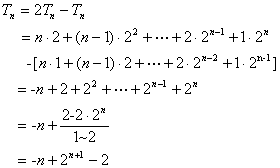
…………12分
解法二：设
。
由（Ⅰ）知
。
∴
…………6分
∴
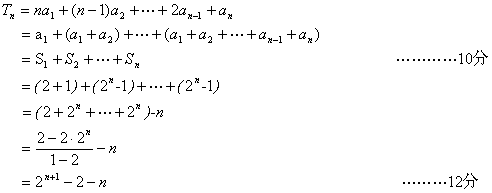
（19）本小题主要考查直线与直线、直线与平面的关系，逻辑推理能力，满分12分。
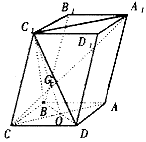（Ⅰ）证明：连结
、
和
交于，连结
。
∵四边形ABCD是菱形，
∴⊥，
=
。
又∵∠=∠
，
=，
∴
，
∴B=D，
∵
∴
，
3分
但
，
∴
平面
。
又
平面，
∴
。
…………6分
（Ⅱ）当
时，能使
平面
。
证明一：
∵，
∴
，
又
，
由此可推得
。
∴三棱锥
是正三棱锥。
…………9分
设
与相交于
。
∵
，且
：
：1，
∴
：
=2：1。
又是正三角形的边上的高和中线，
∴点是正三角形的中心，
∴
平面，
即平面。
…………12分
证明：
由（Ⅰ）知，
平面，
∵
平面，∴
。
…………9分
当时，平行六面体的六个面是全等的菱形，
同的正法可得
。
又
，
∴平面。
…………12分
（20）本小题主要考查不等式的解法、函数的单调性等基本知识，分类讨论的数学思想方法和运算、推理能力，满分12分。
（Ⅰ）解：不等式
即
，
由此得
，即
，其中常数。
所以，原不等式等价于
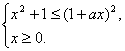
即
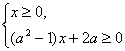…………3分
所以，当
时，所给不等式的解集为
；
当
时，所给不等式的解集为
。
…………6分
（Ⅱ）证明：在区间
上任取
使得
∵
，
∴
，
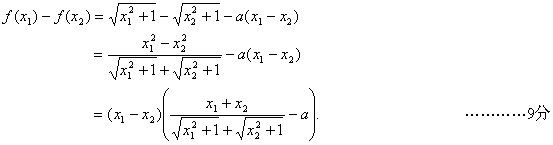
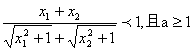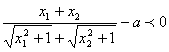又
，
∴
，
即
。
所以，当时，函数在区间上是单调递减函数。 …………12分
（21）本小题主要考查由函数图建立函数关系式和求函数最大值的问题，考查运用所学知识解决实际问题的能力，满分12分。
解：（Ⅰ）由图一可得市场售价与时间的函数关系为
由图二可得种植成本与时间的函数关系为
。
…………4分
（Ⅱ）设
时刻的纯收益为
，则由题意得
=
，
即
=
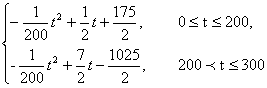…………6分
当
时，配方整理得
=
。
所以，当
时，取得区间[0，200]上的最大值100；
当
时，配方整理得
=
，
所以，当
时，取得区间（200，300）上的最大值87.5 …………10分
综上，由
可知，在区间[0，300]上可以取得最大值100，此时，即从二月一日开始的第50天时，上市的西红柿纯收益最大。
…………12分
（22）本小题主要考查坐标法、定比分点坐标公式、双曲线的概念和性质，推理、运算能力和综合应用数学知识解决问题的能力，满分14分。
解：如图，以AB的垂直平分线为轴，直线AB为轴，建立直角坐标系
，则
轴。
因为双曲线经过点C、D，且以A、B为焦点，由双曲线的对称性知C、D关于轴对称，…………2分
依题意，记
，其中
为双曲线的半焦距，是梯形的高，由定比分点坐标公式得
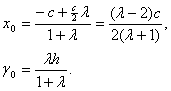
设双曲线的方程为
，则离心率
，由点C、E在双曲线上，将点C、E坐标和代入双曲线的方程，得
，
1
.
2
…………7分
由1式得
，
3
将3式代入2式，整理得
，
故
…………10分
由题设得，
。
解得
，
所以，双曲线的离心率的取值范围为[
]， …………14分