高考数学普通高等学校招生全国统一考试数学57
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。第Ⅰ卷1至2页,第Ⅱ卷3至10页。考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!
第Ⅰ卷(选择题 共60分)
注意事项:
1. 答第Ⅰ卷前,考生务必将自己的姓名、准考号、科目涂写在答题卡上。
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。答在试卷上的无效。
参考公式:
如果事件A、B互斥,那么![]() ,如果事件A、B相互独立,那么
,如果事件A、B相互独立,那么![]() 。
。
柱体(棱柱、圆柱)的体积公式![]()
其中S表示柱体的底面积,h表示柱体的高。
一. 选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)
设集合![]() ,
,![]() ,那么下列结论正确的是
,那么下列结论正确的是
(A)
![]() (B)
(B)
![]()
(C)
![]() (D)
(D)
![]()
![]()
(2)
不等式![]() 的解集为
的解集为
(A)
![]() (B)
(B)
![]()
(C)
![]() (D)
(D)
![]()
(3) 对任意实数a、b、c,在下列命题中,真命题是
(A)“![]() ”是“
”是“![]() ”的必要条件
”的必要条件
(B)“![]() ”是“
”是“![]() ”的必要条件
”的必要条件
(C)“![]() ”是“
”是“![]() ”的充分条件
”的充分条件
(D)“![]() ”是“
”是“![]() ”的充分条件
”的充分条件
(4)
若平面向量![]() 与向量
与向量![]()
![]() 的夹角是
的夹角是![]() ,且
,且![]() ,则
,则![]()
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
(5)
设P是双曲线![]() 上一点,双曲线的一条渐近线方程为
上一点,双曲线的一条渐近线方程为![]() ,
,![]() 、
、![]() 分别是双曲线的左、右焦点。若
分别是双曲线的左、右焦点。若![]() ,则
,则![]()
(A) 1或5 (B) 6 (C) 7 (D) 9
(6)
若函数![]() 在区间
在区间![]() 上的最大值是最小值的3倍,则
上的最大值是最小值的3倍,则![]()
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
(7)
若过定点![]() 且斜率为
且斜率为![]() 的直线与圆
的直线与圆![]() 在第一象限内的部分有交点,则
在第一象限内的部分有交点,则![]() 的取值范围是
的取值范围是
(A)
![]() (B)
(B)
![]()
(C)
![]() (D)
(D)
![]()
(8)
如图,定点A和B都在平面![]() 内,定点
内,定点![]() ,
,![]() ,C是
,C是![]() 内异于A和B的动点,且
内异于A和B的动点,且![]() 。那么,动点C在平面
。那么,动点C在平面![]() 内的轨迹是
内的轨迹是
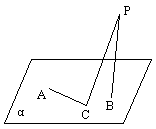
(A) 一条线段,但要去掉两个点 (B) 一个圆,但要去掉两个点
(C) 一个椭圆,但要去掉两个点 (D) 半圆,但要去掉两个点
(9)
函数![]() 的反函数是
的反函数是
(A)
![]() (B)
(B)
![]()
(C)
![]() (D)
(D)
![]()
(10)
函数![]()
![]() 为增函数的区间是
为增函数的区间是
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
(11) 如图,在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() 。分别过BC、
。分别过BC、![]() 的两个平行截面将长方体分成三部分,其体积分别记为
的两个平行截面将长方体分成三部分,其体积分别记为![]() ,
,![]() ,
,![]() 。若
。若![]() ,则截面
,则截面![]() 的面积为
的面积为
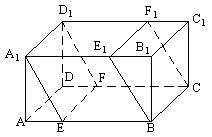
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
(12)
定义在R上的函数![]() 既是偶函数又是周期函数。若
既是偶函数又是周期函数。若![]() 的最小正周期是
的最小正周期是![]() ,且当
,且当![]() 时,
时,![]() ,则
,则![]() 的值为
的值为
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
普通高等学校招生全国统一考试
数学(文史类)
第Ⅱ卷(非选择题 共90分)
注意事项:
1. 用钢笔或圆珠笔直接答在试卷上。
2. 答卷前将密封线内的项目填写清楚。
| 题号 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
| 得分 | ||||||||
二. 填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上。
(13)
某工厂生产A、B、C三种不同型号的产品。产品数量之比依次为![]() 。现用分层抽样方法抽出一个容量为
。现用分层抽样方法抽出一个容量为![]() 的样本,样本中A种型号产品有16件。那么此样本的容量
的样本,样本中A种型号产品有16件。那么此样本的容量![]() 。
。
(14)
已知向量![]() ,
,![]() ,若
,若![]() 与
与![]() 垂直,则实数
垂直,则实数![]() 等于
。
等于
。
(15)
如果过两点![]() 和
和![]() 的直线与抛物线
的直线与抛物线![]() 没有交点,那么实数
没有交点,那么实数![]() 的取值范围是
。
的取值范围是
。
(16) 从0,1,2,3,4,5中任取3个数字,组成没有重复数字的三位数,其中能被5整除的三位数共有 个。(用数字作答)
三. 解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分12分)
已知![]()
(1)求![]() 的值;(2)求
的值;(2)求![]() 的值。
的值。
(18)(本小题满分12分)
从4名男生和2名女生中任选3人参加演讲比赛。
(1)求所选3人都是男生的概率;
(2)求所选3人中恰有1名女生的概率;
(3)求所选3人中至少有1名女生的概率。
(19)(本小题满分12分)
如图,在四棱锥![]() 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱![]() 底面ABCD,
底面ABCD,![]() ,
,![]() 是PC的中点。
是PC的中点。
(1)证明![]() 平面EDB;(2)求EB与底面ABCD所成的角的正切值。
平面EDB;(2)求EB与底面ABCD所成的角的正切值。
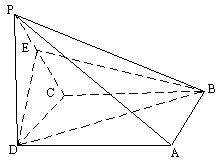
(20)(本小题满分12分)
设![]() 是一个公差为
是一个公差为![]() 的等差数列,它的前10项和
的等差数列,它的前10项和![]() 且
且![]() ,
,![]() ,
,![]() 成等比数列。
成等比数列。
(1)证明![]() ;(2)求公差
;(2)求公差![]() 的值和数列
的值和数列![]() 的通项公式。
的通项公式。
(21)(本小题满分12分)
已知函数![]() 是R上的奇函数,当
是R上的奇函数,当![]() 时
时![]() 取得极值
取得极值![]() 。
。
(1)求![]() 的单调区间和极大值;
的单调区间和极大值;
(2)证明对任意![]() ,
,![]() ,不等式
,不等式![]() 恒成立。
恒成立。
(22)(本小题满分14分)
椭圆的中心是原点O,它的短轴长为![]() ,相应于焦点
,相应于焦点![]()
![]() 的准线
的准线![]() 与
与![]() 轴相交于点A,
轴相交于点A,![]() ,过点A的直线与椭圆相交于P、Q两点。
,过点A的直线与椭圆相交于P、Q两点。
(1)求椭圆的方程及离心率;(2)若![]() ,求直线PQ的方程。
,求直线PQ的方程。
2004年普通高等学校招生全国统一考试(天津卷)
数学(文史类)参考解答
一. 选择题:本题考查基本知识和基本运算,每小题5分,满分60分。
1. D 2. A 3. B 4. A 5. C 6. A 7. A
8. B 9. D 10. C 11. C 12. D
二. 填空题:本题考查基本知识和基本运算。每小题4分,满分16分。
13. 80 14. ![]() 15.
15. ![]() 16.
36
16.
36
三. 解答题
17. 本小题考查两角和正切公式,倍角的正弦、余弦公式等基础知识,考查基本运算能力。满分12分。
(1)
解:![]()
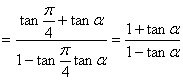
由![]() ,有
,有![]()
解得![]()
(2)
解法一:![]()
![]()
![]()
解法二:由(1),![]() ,得
,得![]()
∴ ![]()
![]()
∴ ![]() 于是
于是![]()
![]()
代入得 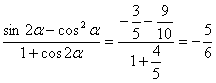
18. 本小题考查等可能事件的概率计算及分析和解决实际问题的能力,满分12分。
(1)解:所选3人都是男生的概率为 ![]()
(2)解:所选3人中恰有1名女生的概率为 ![]()
(3)解:所选3人中至少有1名女生的概率为![]()
19. 本题考查直线与平面平行、直线与平面所成的角等基础知识,考查空间想象能力和推理论证能力,满分12分。
方法一:
(1)证明:连结AC、AC交BD于O。连结EO
∵ 底面ABCD是正方形 ∴ 点O是AC的中点。
在![]() 中,EO是中位线 ∴
中,EO是中位线 ∴ ![]()
而![]() 平面EDB且
平面EDB且![]() 平面
平面![]() ,所以,
,所以,![]() 平面EDB。
平面EDB。
(2)解:作![]() 交CD于F。连结BF,设正方形ABCD的边长为
交CD于F。连结BF,设正方形ABCD的边长为![]() 。
。
∵ ![]() 底面ABCD ∴
底面ABCD ∴ ![]() ∴
∴ ![]() F为DC的中点
F为DC的中点
∴ ![]() 底面ABCD,BF为BE在底面ABCD内的射影,故
底面ABCD,BF为BE在底面ABCD内的射影,故![]() 为直线EB与底面ABCD所成的角。
为直线EB与底面ABCD所成的角。
在![]() 中,
中,![]()
∵ ![]() ∴ 在
∴ 在![]() 中
中 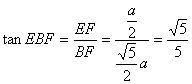
所以EB与底面ABCD所成的角的正切值为![]()
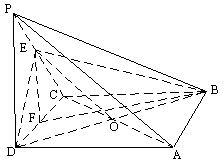
方法二:如图所示建立空间直角坐标系,D为坐标原点。设![]()
(1)证明:连结AC,AC交BD于G。连结EG。依题意得![]() ,
,![]() ,
,
![]() ∵ 底面ABCD是正方形
∵ 底面ABCD是正方形
∴ G是此正方形的中心,故点G的坐标为![]()
∴ ![]()
![]()
∴ ![]() 这表明
这表明![]()
而![]() 平面
平面![]() 且
且![]() 平面EDB
∴
平面EDB
∴ ![]() 平面EDB
平面EDB
(2)解:依题意得![]() ,
,![]()
取DC的中点![]() 连结EF,BF
连结EF,BF
∵ ![]() ,
,![]() ,
,![]()
∴ ![]() ,
,![]() ∴
∴ ![]() ,
,![]()
∴ ![]() 底面ABCD,BF为BE在底面ABCD内的射影,故
底面ABCD,BF为BE在底面ABCD内的射影,故![]() 为直线EB与底面ABCD所成的角。
为直线EB与底面ABCD所成的角。
在![]() 中,
中,![]() ,
,![]()
∴ 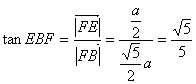
所以,EB与底面ABCD所成的角的正切值为![]() 。
。
20. 本小题主要考查等差数列及其通项公式,等差数列前n项和公式以及等比中项等基础知识,考查运算能力和推理论证能力,满分12分。
(1)证明:因![]() ,
,![]() ,
,![]() 成等比数列,故
成等比数列,故![]()
而![]() 是等差数列,有
是等差数列,有![]() ,
,![]()
于是 ![]()
![]()
即![]()
化简得 ![]()
(2)解:由条件![]() 和
和![]() ,得到
,得到![]()
由(1),![]() ,代入上式得
,代入上式得![]()
故 ![]() ,
,![]()
因此,数列![]() 的通项公式为
的通项公式为![]() ,
,![]() 。
。
21. 本小题主要考查函数的单调性及奇偶性,考查运用导数研究函数单调性及极值等基础知识,考查综合分析和解决问题的能力,满分12分。
(1)解:由奇函数的定义,应有![]() ,
,![]()
即![]() ∴
∴ ![]()
因此,![]()
![]()
由条件![]() 为
为![]() 的极值,必有
的极值,必有![]() ,故
,故![]()
解得![]() ,
,![]()
因此,![]() ,
,![]()
![]()
当![]() 时,
时,![]() ,故
,故![]() 在单调区间
在单调区间![]() 上是增函数
上是增函数
当![]() 时,
时,![]() ,故
,故![]() 在单调区间
在单调区间![]() 上是减函数
上是减函数
当![]() 时,
时,![]() ,故
,故![]() 在单调区间
在单调区间![]() 上是增函数
上是增函数
所以,![]() 在
在![]() 处取得极大值,极大值为
处取得极大值,极大值为![]()
(2)解:由(1)知,![]()
![]() 是减函数,且
是减函数,且
![]() 在
在![]() 上的最大值
上的最大值![]()
![]() 在
在![]() 上的最小值
上的最小值![]()
所以,对任意的![]() ,
,![]() ,恒有
,恒有
![]()
22. 本小题主要考查椭圆的标准方程和几何性质,直线方程,平面向量的计算,曲线和方程的关系等解析几何的基本思想方法和综合解题能力,满分14分。
(1)解:由题意,可设椭圆的方程为![]()
![]()
由已知得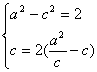 解得
解得![]() ,
,![]()
所以椭圆的方程为![]() ,离心率
,离心率![]()
(2)解:由(1)可得![]() ,设直线PQ的方程为
,设直线PQ的方程为![]() ,由方程组
,由方程组
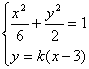 得
得![]()
依题意![]() ,得
,得![]()
设![]() ,
,![]()
则 ![]() ①
① ![]() ②
②
由直线PQ的方程得![]() ,
,![]()
于是 ![]() ③
③
∵ ![]() ∴
∴ ![]() ④
④
由①②③④得![]() ,从而
,从而![]()
所以直线PQ的方程为![]() 或
或![]()