高考数学普通高等学校招生全国统一考试数学91
第Ⅰ卷(选择题共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.函数![]() 的最小正周期是( )
的最小正周期是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设集合![]() ,则满足
,则满足![]() 的集合
的集合![]() 的个数是( )
的个数是( )
A.1 B.3 C.4 D.8
3.设![]() 是
是![]() 上的任意函数,下列叙述正确的是( )
上的任意函数,下列叙述正确的是( )
A.![]() 是奇函数
B.
是奇函数
B.![]() 是奇函数
是奇函数
C.![]() 是偶函数
D.
是偶函数
D.![]() 是偶函数
是偶函数
4.![]() 的值为( )
的值为( )
A.61 B.62 C.63 D.64
5.方程![]() 的两个根可分别作为( )
的两个根可分别作为( )
A.一椭圆和一双曲线的离心率 B.两抛物线的离心率
C.一椭圆和一抛物线的离心率 D.两椭圆的离心率
6.给出下列四个命题:①垂直于同一直线的两条直线互相平行;②垂直于同一平面的两个平面互相平行;③若直线![]() 与同一平面所成的角相等,则
与同一平面所成的角相等,则![]() 互相平行;④若直线
互相平行;④若直线![]() 是异面直线,则与
是异面直线,则与![]() 都相交的两条直线是异面直线,其中假命题的个数是( )
都相交的两条直线是异面直线,其中假命题的个数是( )
A.1 B.2 C.3 D.4
7.双曲线![]() 的两条渐近线与直线
的两条渐近线与直线![]() 围成一个三角形区域,表示该区域的不等式组是( )
围成一个三角形区域,表示该区域的不等式组是( )
A.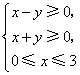 B.
B.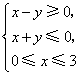 C.
C.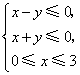 D.
D.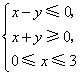
8.设![]() 是
是![]() 上的一个运算,
上的一个运算,![]() 是
是![]() 的非空子集,若对任意
的非空子集,若对任意![]() ,有
,有![]() ,则称
,则称![]() 对运算
对运算![]() 封闭.下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是( )
封闭.下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是( )
A.自然数集 B.整数集 C.有理数集 D.无理数集
9.![]() 的三内角
的三内角![]() 所对边的长分别为
所对边的长分别为![]() .设向量
.设向量![]()
![]() ,
,![]()
![]() .若
.若![]() ,则角
,则角![]() 的大小为( )
的大小为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知等腰![]() 的腰为底的2倍,则顶角
的腰为底的2倍,则顶角![]() 的正切值是( )
的正切值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.与方程![]() 的曲线关于直线
的曲线关于直线![]() 对称的曲线的方程为( )
对称的曲线的方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.曲线![]() 与曲线
与曲线![]() 的( )
的( )
A.离心率相等 B.焦距相等 C.焦点相同 D.准线相同
第II卷(非选择题,共90分)
 二、填空题:本大题共4小题,每小题4分,共16分.
二、填空题:本大题共4小题,每小题4分,共16分.
13.方程![]() 的解为 .
的解为 .
14.设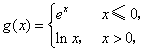 则
则![]() .
.
15.如图,半径为2的半球内有一内接正六棱锥![]() ,则此正六棱锥的侧面积是________.
,则此正六棱锥的侧面积是________.
16.5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1,2,3号参加团体比赛,则入选的3名队员中至少有1名老队员,且1,2号中至少有1名新队员的排法有________种.(以数作答)
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
已知函数![]()
![]() ,求
,求
(1)函数![]() 的最大值及取得最大值的自变量
的最大值及取得最大值的自变量![]() 的集合;
的集合;
(2)函数![]() 的单调增区间.
的单调增区间.
18.(本小题满分12分)
甲、乙两班各派2名同学参加年级数学竞赛,参赛同学成绩及格的概率都为0.6,且参赛同学的成绩相互之间没有影响,求:
(1)甲、乙两班参赛同学中各有1名同学成绩及格的概率;
(2)甲、乙两班参赛同学中至少有1名同学成绩及格的概率.
19.(本小题满分12分)
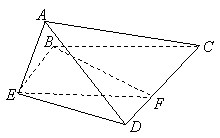
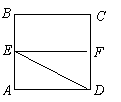
已知正方形![]() ,
,![]() 分别是边
分别是边![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,如图所示,记二面角
折起,如图所示,记二面角![]() 的大小为
的大小为![]() (
(![]() ).
).
(1)证明![]() 平面
平面![]() ;
;
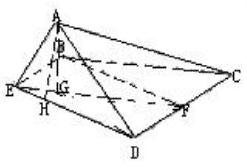
 (2)若
(2)若![]() 为正三角形,试判断点
为正三角形,试判断点![]() 在平面
在平面![]() 内的射影
内的射影![]() 是否在直线
是否在直线![]() 上,证明你的结论,并求角
上,证明你的结论,并求角![]() 的余弦值.
的余弦值.
20.(本小题满分12分)
已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]()
![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 与
与![]() 的等差中项为
的等差中项为![]() ,
,![]() 满足
满足![]() ,求数列
,求数列![]() 的前
的前![]() 项和.
项和.
21.(本小题满分12分)
已知函数![]() ,
,![]() ,其中
,其中![]() ,设
,设![]() 为
为![]() 的极小值点,
的极小值点,![]() 为
为![]() 的极值点,
的极值点,![]() ,并且
,并且![]() ,将点
,将点![]() 依次记为
依次记为![]() .
.
(1)求![]() 的值;
的值;
(2)若四边形![]() 为梯形且面积为1,求
为梯形且面积为1,求![]() 的值.
的值.
22.(本小题满分14分)
已知点![]() 是抛物线
是抛物线![]() 上的两个动点,
上的两个动点,![]() 是坐标原点,向量
是坐标原点,向量![]() 满足
满足![]() ,设圆
,设圆![]() 的方程为
的方程为![]() .
.
(1)证明线段![]() 是圆
是圆![]() 的直径;
的直径;
(2)当圆![]() 的圆心到直线
的圆心到直线![]() 的距离的最小值为
的距离的最小值为![]() 时,求
时,求![]() 的值.
的值.
普通高等学校招生全国统一考试数学
一.选择题:DCCBA DACBD AB
二.填空题:(13)![]() (14)
(14) ![]() (15)
(15) ![]() (16)48
(16)48
三、解答题
(17)本小题考查三角公式、三角函数的性质及已知三角函数值求角等基础知识,考查综合运用三角函数有关知识的能力. 满分 12 分
(I)解法一:![]()
![]()
![]()
![]() ……4分
……4分
![]() 当
当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]()
因此,![]() 取得最大值的自变量x的集合是
取得最大值的自变量x的集合是![]() . ……8分
. ……8分
解法二:![]()
![]()
![]() ……4分
……4分
![]() 当
当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
因此,![]() 取得最大值的自变量x的集合是
取得最大值的自变量x的集合是![]() ……8分
……8分
(Ⅱ)解: ![]()
由题意得![]() ,即
,即![]() .
.
因此, ![]() 的单调增区间是
的单调增区间是![]() .
…………12 分
.
…………12 分
(18)本小题主要考查相互独立事件的概率乘法公式和互斥事件的概率加法等基础知识,考查学生运用概率知识解决实际问题的能力,满分12分.
(Ⅰ)解:甲班参赛同学恰有1名同学成绩及格的概率为![]()
乙班参赛同学中恰有一名同学成绩及格的概率为![]()
故甲、乙两班参赛同学中各有1名同学成绩几个的概率为
![]() …………………………6分
…………………………6分
(Ⅱ)解法一:甲、乙两班4名参赛同学成绩都不及格的概率为![]()
故甲、乙两班参赛同学中至少有一名同学成绩都不及格的概率为
![]() …………………………12分
…………………………12分
解法二:甲、乙两班参赛同学成绩及格的概率为![]()
甲、乙两班参赛同学中恰有2名同学成绩及格的概率为![]()
甲、乙两班参赛同学中恰有3名同学成绩及格的概率为![]()
甲、乙两班4同学参赛同学成绩都及格的概率为![]()
故甲、乙两班参赛同学中至少有1名同学成绩及格的概率为
![]() ……………………12分
……………………12分
(19)本小题主要考查空间中的线面关系,解三角形等基础知识,考查空间想象能力和思维能力.满分12分
(Ⅰ)证明:![]() 、
、![]() 分别是正方形
分别是正方形![]() 的边
的边![]() 、
、![]() 的中点.
的中点.
![]() 且
且![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形 ![]()
![]() 平面
平面![]() 而
而![]() 平面
平面![]()
![]() 平面
平面![]()
 (Ⅱ)解法一:点
(Ⅱ)解法一:点![]() 在平面
在平面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上,过点
上,过点![]() 用
用![]() 平面
平面![]() 垂足为
垂足为![]() 连接
连接![]()
![]() 为正三角形
为正三角形 ![]()
![]()
![]() 在
在![]() 的垂直平分线上。
的垂直平分线上。
又![]()
![]() 是
是![]() 的垂直平分线
的垂直平分线
![]() 点
点![]() 在平面
在平面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上
上
过![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 则
则![]()
![]() 是二面角
是二面角![]() 的平面角,即
的平面角,即![]()
设原正方形![]() 的边长为
的边长为![]() ,连接
,连接![]() ,
,
在折后图的![]() 中,
中,![]()
![]() 为直角三角形,
为直角三角形,![]()
![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
解法二:点![]() 在平面
在平面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上,连结
上,连结![]() ,在平面
,在平面![]() 内过点
内过点![]() 作
作![]() ,垂足为
,垂足为![]()
![]() 为正三角形,
为正三角形,![]() 为
为![]() 的中点,
的中点,![]()
又![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
![]()
又![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 为
为![]() 在平面
在平面![]() 内的射影
内的射影![]() 。
。
![]() 点
点![]() 在平面
在平面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上
上
过![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,则
,则![]() ,
,
![]() 是二面角
是二面角![]() 的平面角,即
的平面角,即![]()
设原正方形![]() 的边长为
的边长为![]() 。
。
在折后图的![]() 中,
中,![]() ,
,![]()
![]() 为直角三角形,
为直角三角形,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]()
![]()
解法三:点![]() 在平面
在平面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上 连结
上 连结![]() ,在平面
,在平面![]() 内过点
内过点![]() 作
作![]() ,垂足为
,垂足为![]()
![]() 为正三角形,
为正三角形,![]() 为
为![]() 的中点
的中点 ![]()
又![]()
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() 平面
平面![]()
又![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,即
,即![]() 为
为![]() 在平面
在平面![]() 内的射影
内的射影![]() ,
,
![]() 点
点![]() 在平面
在平面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上。
上。
过![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,则
,则![]()
![]() 是二面角
是二面角![]() 的平面角,即
的平面角,即![]()
设原正方形![]() 的边长为
的边长为![]()
在折后图的![]() 中,
中,![]()
![]() .
.
![]()
![]() 为直角三角形,
为直角三角形,![]() .
. ![]()
![]() .
.
在![]() 中,
中,![]() ,
, ![]() ,
, ![]() ,
, ![]() .········12分
.········12分
(20) 本小题考查数列的概念,等差数列,等比数列,对数与指数互相转化等基础知识。考查综合运用数学知识解决问题的能力。满分 12 分.
(Ⅰ) 解法一:当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
![]() .
.
![]() 是等差数列,
是等差数列,![]() ,
, ![]() ············4分
············4分
解法二:当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
![]() .
.
当![]() 时,
时,![]() .
.
![]() .
.
又![]() ,所以
,所以![]() ,得
,得 ![]() . ············4分
. ············4分
(Ⅱ) 解:![]() ,
, ![]() . 又
. 又![]() ,
, ![]() ,
,
![]()
![]() ············8分
············8分
又![]() 得
得 ![]() .
.
![]() ,
,![]() ,即
,即 ![]() 是等比数列.
是等比数列.
所以数列![]() 的前
的前![]() 项和
项和![]() .
···········12分
.
···········12分
(21) (Ⅰ) 解:![]() ,
,
令![]() ,由
,由![]() 得
得![]() 或
或![]() .
············2分
.
············2分
![]() .
. ![]()
![]()
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() , 所以
, 所以![]() 处取极小值,即
处取极小值,即![]() ....................6分
....................6分
(II)解:![]()
![]()
![]() 处取得极小值,即
处取得极小值,即![]()
由![]() 即
即![]()
![]()
![]()
![]()
![]()
![]() ................9分
................9分
由四边形ABCD是梯形及BC与AD不平行,得![]() .
.
![]() 即
即![]() 由四边形ABCD的面积为1,得
由四边形ABCD的面积为1,得![]()
即![]() 得d=1,从而
得d=1,从而![]() 得
得![]() ....................12分
....................12分
(22)本小题主要考查平面向量的基本运算,圆与抛物线的方程,点到直线的距离等基础知识,以及综合运用解析几何知识解决问题的能力,满分14分。
(I)证法一:![]()
![]() 即
即![]()
整理得![]()
![]() ......................12分
......................12分
设点M(x,y)是以线段AB为直径的圆上的任意一点,则![]()
即![]()
展开上式并将①代入得![]() 故线段
故线段![]() 是圆
是圆![]() 的直径。
的直径。
证法二:![]()
![]()
即![]() ,
,
整理得![]()
![]() ①
……3分
①
……3分
若点![]() 在以线段
在以线段![]() 为直径的圆上,则
为直径的圆上,则![]()
去分母得![]()
点![]() 满足上方程,展开并将①代入得
满足上方程,展开并将①代入得
![]() 所以线段
所以线段![]() 是圆
是圆![]() 的直径.
的直径.
证法三:![]()
![]()
![]()
即![]() , 整理得
, 整理得![]()
![]()
以![]() 为直径的圆的方程是
为直径的圆的方程是![]()
展开,并将①代入得![]() 所以线段
所以线段![]() 是圆
是圆![]() 的直径.
的直径.
(Ⅱ)解法一:设圆![]() 的圆心为
的圆心为![]() ,则
,则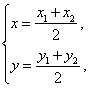
![]() ,
,![]()
又![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
所以圆心的轨迹方程为:![]()
设圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则![]()
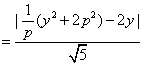
![]()
当![]() 时,
时,![]() 有最小值
有最小值![]() ,由题设得
,由题设得![]()
![]()
![]() ……14 分
……14 分
解法二:设圆![]() 的圆心为
的圆心为![]() ,则
,则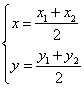
![]()
![]()
又 ![]()
![]()
![]() …………9 分
…………9 分
![]()
![]()
![]()
![]()
所以圆心得轨迹方程为![]() …………11分 设直线
…………11分 设直线![]() 与
与![]() 的距离为
的距离为 ![]() ,则
,则![]()
因为![]() 与
与![]() 无公共点.
无公共点.
所以当![]() 与
与![]() 仅有一个公共点时,
该点到
仅有一个公共点时,
该点到![]() 的距离最小,最小值为
的距离最小,最小值为 ![]()
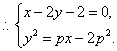
将②代入③![]() ,有
,有 ![]() …………14 分
…………14 分
解法三:设圆![]() 的圆心为
的圆心为![]() ,则
,则 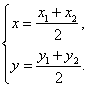
若圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,那么
,那么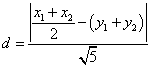
![]()
![]()
又 ![]()
![]()
![]()
![]()
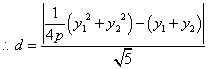
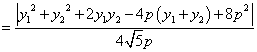
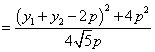
当![]() 时,
时,![]() 有最小值时
有最小值时![]() ,由题设得
,由题设得 ![]()
![]()