高考数学普通高等学校招生全国统一考试数学118含答案
理科试题(必修+选修II)
注意事项:
1.本试卷分第一部分和第二部分。第一部分为选择题,第二部分为非选择题。
2.考生领到试卷后,须按规定在试卷上填写姓名、准考证号,并在答题卡上填涂对应的试卷类型信息点。
3.所有答案必须在答题卡上指定区域内作答。考试结束后,将本试卷和答题卡一并交回。
第一部分(共60分)
一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本大题共12小题,每小题5分,共60分)
1.已知集合![]() 集合
集合![]() 则
则![]() 等于
等于
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.复数![]() 等于
等于
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.![]() 等于
等于
(A)0 (B)![]() (C)
(C)![]() (D)
(D)![]()
4.设函数![]() 的图像过点
的图像过点![]() ,其反函数的图像过点
,其反函数的图像过点![]() ,则
,则![]() 等于
等于
(A)3 (B)4 (C)5 (D)6
5.设直线过点![]() 其斜率为1,且与圆
其斜率为1,且与圆![]() 相切,则
相切,则![]() 的值为
的值为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.![]() 等式
等式![]() 成立
成立![]() 是
是![]()
![]() 成等差数列
成等差数列 ![]() 的
的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分又不必要条件
7.已知双曲线![]() 的两条渐近线的夹角为
的两条渐近线的夹角为![]() ,则双曲线的离心率为
,则双曲线的离心率为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)2
(D)2
8.已知不等式![]() 对任意正实数
对任意正实数![]() 恒成立,则正实数
恒成立,则正实数![]() 的最小值为
的最小值为
(A)8 (B)6 (C)4 (D)2
9.已知非零向量![]() 与
与![]() 满足
满足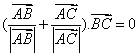 且
且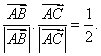 则
则![]() 为
为
(A)等边三角形 (B)直角三角形
(C)等腰非等边三角形 (D)三边均不相等的三角形
10.已知函数![]() 若
若![]() 则
则
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]() 与
与![]() 的大小不能确定
的大小不能确定
11.已知平面![]() 外不共线的三点
外不共线的三点![]() 到
到![]() 的距离都相等,则正确的结论是
的距离都相等,则正确的结论是
(A)平面ABC必不垂直于![]() (B)平面ABC必平行于
(B)平面ABC必平行于![]()
(C)平面ABC必与![]() 相交
相交
(D)存在![]() 的一条中位线平行于
的一条中位线平行于![]() 或在
或在![]() 内
内
12.为确保信息安全,信息需加密传输,发送方由明文![]() 密文(加密),接收方由密文
密文(加密),接收方由密文![]() 明文(解密),已知加密规则为:明文
明文(解密),已知加密规则为:明文![]() 对应密文
对应密文![]() 例如,明文
例如,明文![]() 对应密文
对应密文![]() 当接收方收到密文
当接收方收到密文![]() 时,则解密得到的明文为
时,则解密得到的明文为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
第二部分(共90分)
二.填空题:把答案填在答题卡相应题号后的横线上(本大题共4小题,每小题4分,共16分)。
13.![]() 的值为______。
的值为______。
14.![]() 展开式中
展开式中![]() 的常数项为_____(用数字作答)。
的常数项为_____(用数字作答)。
15.水平桌面![]() 上放有4个半径均为2R的球,且相邻的球都相切(球心的连线构成正方形)。在这4个球的上面放一个半径为R的小球,它和下面的4个球恰好相切,则小球的球心到水平桌面
上放有4个半径均为2R的球,且相邻的球都相切(球心的连线构成正方形)。在这4个球的上面放一个半径为R的小球,它和下面的4个球恰好相切,则小球的球心到水平桌面![]() 的距离是____。
的距离是____。
16.某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,甲和丙只能同去或同不去,则不同的选派方案共有_____种(用数字作答)。
三.解答题:解答应写出文字说明,证明过程或演算步骤(本大题共6小题,共74分)。
(17)(本小题满分12分)
已知函数![]()
(I)求函数![]() 的最小正周期;
的最小正周期;
(II)求使函数![]() 取得最大值的
取得最大值的![]() 集合。
集合。
(18)(本小题满分12分)
甲、乙、丙3人投篮,投进的概率分别是![]()
(I)现3人各投篮1次,求3人都没有投进的概率;
(II)用![]() 表示投篮3次的进球数,求随机变量
表示投篮3次的进球数,求随机变量![]() 的概率分布及数学期望
的概率分布及数学期望![]()
(19)(本小题满分12分)
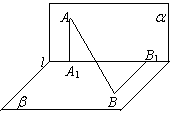 如图,
如图,![]() 点A在直线
点A在直线![]() 上的射影为
上的射影为![]() 点B在
点B在![]() 上的射影为
上的射影为![]() 已知
已知![]() 求:
求:
(I)直线AB分别与平面![]() 所成角的大小;
所成角的大小;
(II)二面角![]() 的大小。
的大小。
(20)(本小题12分)
已知正项数列![]() ,其前
,其前![]() 项和
项和![]() 满足
满足![]() 且
且![]() 成等比数列,求数列
成等比数列,求数列![]() 的通项
的通项![]()
(21)(本小题满分为12分)
如图,三定点![]() 三动点D、E、M满足
三动点D、E、M满足

![]()
![]()
(I)求动直线DE斜率的变化范围;
(II)求动点M的轨迹方程。
(22)(本小题满分14分)
已知函数![]() 且存在
且存在![]() 使
使![]()
(I)证明:![]() 是R上的单调增函数;
是R上的单调增函数;
设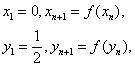 其中
其中 ![]()
(II)证明:![]()
(III)证明:![]()
参考答案
一、选择题
1.B 2.C 3.B 4.C 5.B 6.A 7.D 8.B 9.D
10.A 11.D 12.C
二、填空题
13.- 14.594 15.3R 16.600
三、解答题
17.解:(Ⅰ) f(x)=sin(2x-)+1-cos2(x-)
= 2[sin2(x-)- cos2(x-)]+1
=2sin[2(x-)-]+1
= 2sin(2x-) +1
∴ T==π
(Ⅱ)当f(x)取最大值时, sin(2x-)=1,有 2x- =2kπ+
即x=kπ+ (k∈Z) ∴所求x的集合为{x∈Rx= kπ+ , (k∈Z)}.
18.解: (Ⅰ)记"甲投篮1次投进"为事件A1 , "乙投篮1次投进"为事件A2 , "丙投篮1次投进"为事件A3, "3人都没有投进"为事件A . 则 P(A1)= , P(A2)= , P(A3)= ,
∴ P(A) = P()=P()·P()·P()
= [1-P(A1)] ·[1-P (A2)] ·[1-P (A3)]=(1-)(1-)(1-)=
∴3人都没有投进的概率为 .
(Ⅱ)解法一: 随机变量ξ的可能值有0,1,2,3), ξ~ B(3, ),
P(ξ=k)=C3k()k()3-k (k=0,1,2,3) , Eξ=np = 3× = .
解法二: ξ的概率分布为:
| ξ | 0 | 1 | 2 | 3 |
| P |
Eξ=0×+1×+2×+3×= .
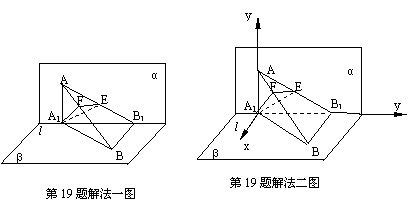

19.解法一: (Ⅰ)如图, 连接A1B,AB1, ∵α⊥β, α∩β=l ,AA1⊥l, BB1⊥l,
∴AA1⊥β, BB1⊥α. 则∠BAB1,∠ABA1分别是AB与α和β所成的角.
Rt△BB1A中, BB1= , AB=2, ∴sin∠BAB1 = = . ∴∠BAB1=45°.
Rt△AA1B中, AA1=1,AB=2, sin∠ABA1= = , ∴∠ABA1= 30°.
故AB与平面α,β所成的角分别是45°,30°.
(Ⅱ) ∵BB1⊥α, ∴平面ABB1⊥α.在平面α内过A1作A1E⊥AB1交AB1于E,则A1E⊥平面AB1B.过E作EF⊥AB交AB于F,连接A1F,则由三垂线定理得A1F⊥AB, ∴∠A1FE就是所求二面角的平面角.
在Rt△ABB1中,∠BAB1=45°,∴AB1=B1B=. ∴Rt△AA1B中,A1B== = . 由AA1·A1B=A1F·AB得 A1F== = ,
∴在Rt△A1EF中,sin∠A1FE = = , ∴二面角A1-AB-B1的大小为arcsin.
解法二: (Ⅰ)同解法一.
(Ⅱ) 如图,建立坐标系, 则A1(0,0,0),A(0,0,1),B1(0,1,0),B(,1,0).在AB上取一点F(x,y,z),则存在t∈R,使得=t , 即(x,y,z-1)=t(,1,-1), ∴点F的坐标为(t, t,1-t).要使⊥,须·=0, 即(t, t,1-t) ·(,1,-1)=0, 2t+t-(1-t)=0,解得t= , ∴点F的坐标为(,-, ), ∴=(,, ). 设E为AB1的中点,则点E的坐标为(0,, ). ∴=(,-,).
又·=(,-,)·(,1,-1)= - - =0, ∴⊥, ∴∠A1FE为所求二面角的平面角.
又cos∠A1FE= = = = = ,
∴二面角A1-AB-B1的大小为arccos.
20.解: ∵10Sn=an2+5an+6, ① ∴10a1=a12+5a1+6,解之得a1=2或a1=3.
又10Sn-1=an-12+5an-1+6(n≥2),②
由①-②得 10an=(an2-an-12)+6(an-an-1),即(an+an-1)(an-an-1-5)=0
∵an+an-1>0 , ∴an-an-1=5 (n≥2).
当a1=3时,a3=13,a15=73. a1, a3,a15不成等比数列∴a1≠3;
当a1=2时, a3=12, a15=72, 有 a32=a1a15 , ∴a1=2, ∴an=5n-3.
21.解法一: 如图, (Ⅰ)设D(x0,y0),E(xE,yE),M(x,y).由=t, = t , 知(xD-2,yD-1)=t(-2,-2). ∴ 同理 . ∴kDE = = = 1-2t.
∴t∈[0,1] , ∴kDE∈[-1,1].
(Ⅱ) ∵=t ∴(x+2t-2,y+2t-1)=t(-2t+2t-2,2t-1+2t-1)=t(-2,4t-2)=(-2t,4t2-2t). ∴ , ∴y= , 即x2=4y. ∵t∈[0,1], x=2(1-2t)∈[-2,2].
即所求轨迹方程为: x2=4y, x∈[-2,2]
解法二: (Ⅰ)同上.
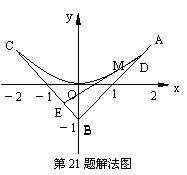 (Ⅱ) 如图, =+ = + t = + t(-) = (1-t) +t,
(Ⅱ) 如图, =+ = + t = + t(-) = (1-t) +t,
= + = +t = +t(-) =(1-t) +t,
= += + t= +t(-)=(1-t) + t
= (1-t2) + 2(1-t)t+t2 .
设M点的坐标为(x,y),由=(2,1), =(0,-1), =(-2,1)得
消去t得x2=4y, ∵t∈[0,1], x∈[-2,2].
故所求轨迹方程为: x2=4y, x∈[-2,2]
22.解: (I)∵f '(x)=3x2-2x+ = 3(x-)2+ >0 , ∴f(x)是R上的单调增函数.
(II)∵0<x0< , 即x1<x0<y1.又f(x)是增函数, ∴f(x1)<f(x0)<f(y1).即x2<x0<y2.
又x2=f(x1)=f(0)=>0 =x1, y2=f(y1)=f()=<=y1,综上, x1<x2<x0<y2<y1.
用数学归纳法证明如下:
(1)当n=1时,上面已证明成立.
(2)假设当n=k(k≥1)时有xk<xk+1<x0<yk+1<yk .
当n=k+1时,由f(x)是单调增函数,有f(xk)<f(xk+1)<f(x0)<f(yk+1)<f(yk),∴xk+1<xk+2<x0<yk+2<yk+1
由(1)(2)知对一切n=1,2,…,都有xn<xn+1<x0<yn+1<yn.
(III) = = yn2+xnyn+xn2-(yn+xn)+ ≤(yn+xn)2-(yn+xn)+
=[(yn+xn)-]2+ . 由(Ⅱ)知 0<yn+xn<1.∴- < yn+xn- < ,
∴ < ()2+ = .