高考数学普通高等学校招生全国统一考试文科数学（Ⅱ）
第Ｉ卷（共60分）
一．选择题
1、已知向量
＝（4，2），向量
＝（
，3），且//,则＝
（A）9 (B)6 (C)5 (D)3
2、已知集合
，则
（A）
（B）
（C）
（D）
3、函数
的最小正周期是
（A）
（B）
（C）
（D）
4、如果函数
的图像与函数
的图像关于坐标原点对称，则的表达式为
（A）
（B）
（C）
（D）
5、已知
的顶点B、C在椭圆
上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则的周长是
（A）
（B）6 （C）
（D）12
6、已知等差数列
中，
，则前10项的和
＝
（A）100 (B)210 (C)380 (D)400
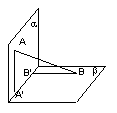
7、如图，平面
平面
，
与两平面
、所成的角分别为
和
。过A、B分别作两平面交线的垂线，垂足为
、
若AB=12,则
（A）4 （B）6 （C）8 （D）9
8、已知函数
，则
的反函数为
（A）
（B）
（C）
（D）
9、已知双曲线
的一条渐近线方程为
，则双曲线的离心率为
（A）
（B）
（C）
（D）
10、若
则
（A）
（B）
（C）
（D）
11、过点（－1，0）作抛物线
的切线，则其中一条切线为
（A）
（B）
（C）
（D）
12、5名志愿者分到3所学校支教，每个学校至少去一名志愿者，则不同的分派方法共有
（A）150种 (B)180种 (C)200种 (D)280种
第Ⅱ卷（非选择题，共90分）
二．填空题：本大题共４小题，每小题４分，共１６分，把答案填在横线上。
13、在
的展开式中常数项是＿＿＿＿＿。（用数字作答）
14、圆
是以
为半径的球
的小圆，若圆的面积
和球的表面积
的比为
，则圆心到球心的距离与球半径的比
＿＿＿＿＿。
15、过点
的直线
将圆
分成两段弧，当劣弧所对的圆心角最小时，直线的斜率
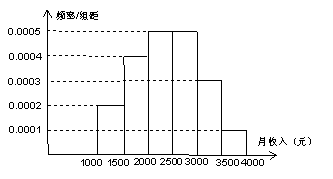
16、一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（如下图）。为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，则在
（元）月收入段应抽出＿＿＿＿＿人。
三．解答题：本大题共６小题，共７４分。解答应写出文字说明，证明过程或演算步骤。
17、（本小题满分１２分）
在
,
（I）求
边的长；
（II）若点
18、（本小题满分１２分）
设等比数列的前n项和为
，
19、（本小题满分１２分）
某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，再从每箱中任意出取2件产品进行检验。设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品。
（I）求取6件产品中有1件产品是二等品的概率。
（II）若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批产品被用户拒绝的概率。
20、（本小题满分为１２分）
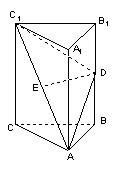
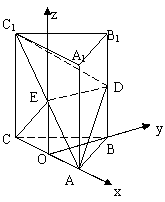
如图，在直三棱柱
中，
、
分别为
、
的中点。
（I）证明：ED为异面直线与的公垂线；
（II）设
求二面角
的大小
21、（本小题满分为１４分）
设
，函数
若
的解集为A，
，求实数
的取值范围。
22、（本小题满分１２分）
已知抛物线
的焦点为F，A、B是抛物线上的两动点，且
过A、B两点分别作抛物线的切线，设其交点为M。
（I）证明
为定值；
（II）设
的面积为S，写出
的表达式，并求S的最小值。
2006普通高等学校招生全国统一考试文科数学（Ⅱ）参考答案
一、选择题：BDDDC BBBAC DA
二、填空题：13、45 14、
15、
16、25。
三、解答题：
17、解：由
， 
由正弦定理知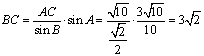
………………………………
6分
（Ⅱ）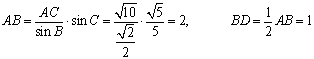
…………………… 9分
由余弦定理知
……12分
18、解：设{
} 的公比为q ，由
知q ≠1 ，所以得
……………………① 
…………………………②
由①、②得
………………………………8分
将q = 2 代入①得
所以
将q = - 2 代入①得
所以
……………………………………12分
19、解：设A i 表示事件“第二箱中取出i件二等品”，i = 0，1；
B i 表示事件“第三箱中取出i件二等品”，i = 0，1，2。
（Ⅰ）依题意所求的概率为
（Ⅱ）解法一：设所求的概率为
…………………… 12分
解法二；所求概率为
……………………………
12分
20、解法一：（Ⅰ）设O为AC中点，连结EO，BO，则EO
又CC1 B1B，
所以EODB ，则EOBD为平行四边形， ED∥OB
…………………… 2分
∵ AB = BC，∴
BO⊥AC ，又面ABC⊥面ACC1A1，BO
面ABC ，故BO⊥面ACC1A1
∴ ED⊥面ACC1A1，ED⊥AC1，ED⊥CC1 ∴ ED⊥BB1
ED为异面直线AC1与BB1的公垂线 ………………………… 6分
（Ⅱ）联结A1E，由AA1 = AC = 
AB可知，A1ACC1为正方形，
∴ A1E ⊥AC1 由ED⊥面A1ACC1和ED面ADC1知面ADC1⊥面A1ACC1
ED⊥A1E
则A1E⊥面ADE。 过E向AD作垂线，垂足为F，连结A1F，
由三垂线定理知∠A1FE为二面角A1—AD—C1的平面角。
不妨设AA1 = 2 ，则AC = 2 ，AB
= ， ED = OB = 1 ，
EF
=
所以二面角A1—AD—C1为60°…………………………………… 12分
解法二：如图建立直角坐标系O—xyz，其中原点O为AC中点。
设A（a，0，0），B（0，b，0），B1（0，b，2c），则C（- a，0，0），
C1（- a，0，c），E（0，0，c）D（0，b，c） …………………… 3分
又
所以ED是异面直线BB1与AC1公垂线。
（Ⅱ）不妨设A（1，0，0），则B（0，1，0），C（-1，0，0），A1（1，0，2）
即BC⊥AB，BC⊥AA1，又
∴ BC⊥面A1AD。
又 E（0，0，1），D（0，1，1），C（-1，0，0）
即EC⊥AE， EC⊥ED
，又AE∩ED
= E
∴ EC⊥面C1AD ………………………………………………………… 10 分
即得
和
的夹角为60°。
所以二面角A1—AD—C1为60°。 ……………………………………… 12 分
21、解：由f（x）为二次函数知a ≠
0 ，令f（x）= 0解得两根为
由此可知x1< 0 , x 2 > 0
①当a
> 0 时，A = {x x < x 1}∪{x x > x 2}，A∩B
≠Φ的充要条件是x 2 < 3，即
(6分)
②当a
< 0 时，A = { x x 1< x <
x 2 },A∩B ≠Φ的充要条件是x 2 > 1 , 即
(10分)
综上，使A∩B
≠Φ成立的a 的取值范围为
………………………… 12分。
22、解：（Ⅰ）由已知条件，得F（0，1），设A（x1，y1），B（x2，y2），
由
得
将（1）式两边平方并把
代入
得
（3）。 解（2）、（3）得
由
。由抛物线方程为
，求导得
所以过抛物线上A、B两点的切线方程分别是
即
解出两条切线的交点M的坐标为
所以
所以为定值。
（Ⅱ）由（Ⅰ）知在△ABM中，FM⊥AB，因而S = 
于是 
由 
知
当且仅当 
时，S
取得最小值 4 。 …………………………………………………… 14 分