高考数学普通高等学校招生全国统一考试111
数学试题(理工农医类)共5页,满分150分。考试时间120分钟。
注意事项:
1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3.答非选择题时,必须使0.5毫米黑色墨水签字笔,将答案书写在答题止规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
5.考试结束,监考员将试题卷和答题卡一并收回。
参考公式:
如果事件A、B互斥,那么P(A+B)-P(A)+P(B) .
如果事件A、B相互独立,那么P(A·B)-P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立事件重复试验中恰好发生k次的概率Pn(k)=CknPk(1-P)n-k
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)已知集合U={1,2,3,4,5,6,7}, A={2,4,5,7},B={3,4,5},则(![]() uA)∪(
uA)∪(![]() uB)=
uB)=
(A){1,6} (B){4,5}
(C){1,2,3,4,5,7} (D){1,2,3,6,7}
(2)在等差数列{an}中,若aa+ab=12,SN是数列{an}的前n项和,则SN的值为
(A)48 (B)54 (C)60 (D)66
(3)过坐标原点且与x2|y2 4x|2y+![]() =0相切的直线的方程为
=0相切的直线的方程为
(A)y=-3x或y=![]() x
(B) y=-3x或y=-
x
(B) y=-3x或y=-![]() x
x
(C)y=-3x或y=-![]() x
(B) y=3x或y=
x
(B) y=3x或y=![]() x
x
(4)对于任意的直线l与平同a,在平面a内必有直线m,使m与l
(A)平行 (B)相交
(C)垂直 (D)互为异面直线
(5)若![]()
![]() n的展开式中各项系数之和为64,则展开式的常数项为
n的展开式中各项系数之和为64,则展开式的常数项为
(A)-540 (B)
(c)162 (D)540
(6)为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下:
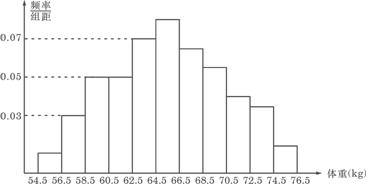
根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是
(A)20 (B)30
(C)40 (D)50
(7)与向量a=![]()
![]() 的夹解相等,且模为1的向量是
的夹解相等,且模为1的向量是
(A) ![]() (B)
(B)
![]() 或
或![]()
(C)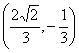 (D)
(D)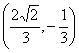 或
或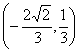
(8)将5名实习教师分配到高一年级的3个班实习,每班至少1名,最多2名,则不同的分配方案有
 (A)30种 (B)90种
(A)30种 (B)90种
(C)180种 (D)270种
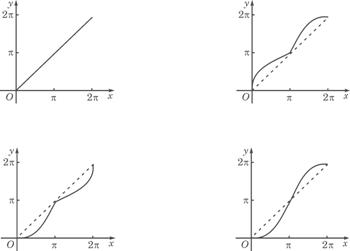
(9)如图所示,单位圆中弧AB的长为x,f(x)表示弧AB与弦AB
所围成的弓形面积的2倍,则函数y=f(x)的图象是
题 (9)图
(10)若a,b,c>0且a(a+b+c)+bc=4-2![]() ,则2a+b+c的最小值为
,则2a+b+c的最小值为
(A)![]() -1
(B)
-1
(B) ![]() +1
+1
(C) 2![]() +2
(D) 2
+2
(D) 2![]() -2
-2
一、填空题:本大题共6小题,共24分,把答案填写在答题卡相应位置上
(11)复数复数![]() 的值是_________.
的值是_________.
(12)![]()
![]() _________.
_________.
(13)已知![]()
![]() ,sin(
,sin(![]() )=-
)=-![]() sin
sin![]() 则os
则os![]() =________.
=________.
(14)在数列{an}中,若a1=1,an+1=2an+3 (n≥1),则该数列的通项an=_________.
(15)设a>0,n![]() 1,函数f(x)=alg(x2-2n+1)
有最大值.则不等式logn(x2-5x+7)
>0的解集为_______.
1,函数f(x)=alg(x2-2n+1)
有最大值.则不等式logn(x2-5x+7)
>0的解集为_______.
(16)已知变量x,y满足约束条件1≤x+y≤4,-2≤x-y≤2.若目标函数z=ax+y(其中a>0)仅在点(3,1)处取得最大值,则a的取值范围为___________.
二、解答题:本大题共6小题,共76分解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分13分)
设函数f(x)=![]() cos2cos+sin
cos2cos+sin![]() rcos
rcos![]() x+a(其中
x+a(其中![]() >0,a
>0,a![]() R),且f(x)的图象在y轴右侧的第一个高点的横坐标为
R),且f(x)的图象在y轴右侧的第一个高点的横坐标为![]() .
.
(Ⅰ)求ω的值;
(Ⅱ)如果f(x)在区间![]() 上的最小值为
上的最小值为![]() ,求a的值.
,求a的值.
(18)(本小题满分13分)
某大厦的一部电梯从底层出发后只能在第18、19、20层可以停靠.若该电梯在底层载有![]() 5
5
位乘客,且每位乘客在这三层的每一层下电梯的概率均为![]() ,用ξ表示这5位乘客在第20层下电梯的人数.求:
,用ξ表示这5位乘客在第20层下电梯的人数.求:
(Ⅰ)随机变量ξ的分布列;
(Ⅱ)随机变量ξ的期望.
(19)(本小题满分13分)
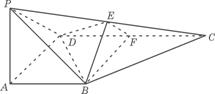
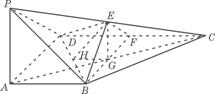
如图,在四棱锥P-ABCD中,PA![]() 底面ABCD,
底面ABCD,![]() DAB为直角,AB‖CD,AD=CD=24B,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=24B,E、F分别为PC、CD的中点.
 (Ⅰ)试证:CD
(Ⅰ)试证:CD![]() 平面BEF;
平面BEF;
(Ⅱ)设PA=k·AB,且二面角E-BD-C的平面角大于![]() ,求k的取值范围.
,求k的取值范围.
(20)(本小题满分13分)
已知函数f(x)=(x2+bx+c)cx,其中b,c![]() R为常数. 图(19)图
R为常数. 图(19)图
(Ⅰ)若b2>4(a-1),讨论函数f(x)的单调性;
(Ⅱ)若b2<4(c-1),且![]()
![]() =4,试证:-6≤b≤2.
=4,试证:-6≤b≤2.
(21)(本小题满分12分)
已知定义域为R的函数f(x)满足f(f(x)-x2+y_=f(x)-x2+x.
(Ⅰ)若f(2)-3,求f(1);又若f(0)=a,求f(a);
(Ⅱ)设有且仅有一个实数x0,使得f(x0)= x0,求函数f(x)的解析表达式.
(22)(本小题满分12分)
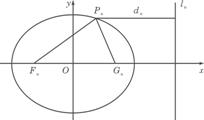
已知一列椭圆Cn:x2+![]() =1. 0<bn<1,n=1,2.
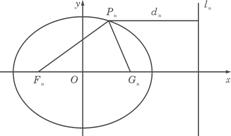
=1. 0<bn<1,n=1,2.![]() .若椭圆C上有一点Pn使Pn到右准线ln的距离d.是|PnFn|与|PnCn|的等差中项,其中Fn、Cn分别是Cn的左、右焦点.
.若椭圆C上有一点Pn使Pn到右准线ln的距离d.是|PnFn|与|PnCn|的等差中项,其中Fn、Cn分别是Cn的左、右焦点.
 (Ⅰ)试证:bn≤
(Ⅰ)试证:bn≤![]() (n≥1);
(n≥1);
(Ⅱ)取bn=![]() ,并用SA表示
,并用SA表示![]() PnFnGn的面积,试证:S1<S1且Sn<Sn+3 (n≥3).
PnFnGn的面积,试证:S1<S1且Sn<Sn+3 (n≥3).
图(22)图
(20)(本小题满分13分)
已知函数f(x)=(x2+bx+c)cx,其中b,c![]() R为常数.
R为常数.
(Ⅰ)若b2>4(a-1),讨论函数f(x)的单调性;
(Ⅱ)若b2<4(c-1),且![]()
![]() =4,试证:-6≤b≤2.
=4,试证:-6≤b≤2.
(21)(本小题满分12分)
已知定义域为R的函数f(x)满足f(f(x)-x2+y_=f(x)-x2+x.
(Ⅰ)若f(2)-3,求f(1);又若f(0)=a,求f(a);
(Ⅱ)设有且仅有一个实数x0,使得f(x0)= x0,求函数f(x)的解析表达式.
(22)(本小题满分12分)
已知一列椭圆Cn:x2+![]() =1. 0<bn<1,n=1,2.
=1. 0<bn<1,n=1,2.![]() .若椭圆C上有一点Pn使Pn到右准线ln的距离d.是|PnFn|与|PnCn|的等差中项,其中Fn、Cn分别是Cn的左、右焦点.
.若椭圆C上有一点Pn使Pn到右准线ln的距离d.是|PnFn|与|PnCn|的等差中项,其中Fn、Cn分别是Cn的左、右焦点.
(Ⅰ)试证:bn≤![]() (n≥1);
(n≥1);
(Ⅱ)取bn=![]() ,并用SA表示
,并用SA表示![]() PnFnGn的面积,试证:S1<S1且Sn<Sn+3 (n≥3).
PnFnGn的面积,试证:S1<S1且Sn<Sn+3 (n≥3).
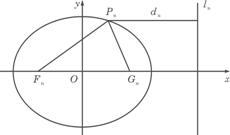
图(22)图
(18)(本小题13分)
解法一:(Ⅰ)ξ的所有可能值为0,1,2,3,4,5.
由等可能性事件的概率公式得
P(ξ=0)=![]() =
=![]() ,
P(ξ=1)=
,
P(ξ=1)= ![]()
![]()
P(ξ=2)= ![]() =
=![]() , P(ξ=3)=
, P(ξ=3)= ![]()
![]()
P(ξ=4)= ![]() =
=![]() , P(ξ=5)=
, P(ξ=5)= ![]()
![]()
从而ξ的分布列为
| ξ | 0 | 1 | 2 | 3 | 4 | 5 |
| P |
|
|
|
|
|
|
(Ⅱ)由(Ⅰ)得ξ的期望为
Eξ=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() +4×
+4×![]() +5×
+5×![]()
=![]() =
=![]() .
.
解法二:(Ⅰ)考察一位乘客是否在第20层下电梯为一次试验,这是5次独立重复试验.
故ξ-B![]() ,即有
,即有
P(ξ=k)=C![]()
![]()
![]() ,k=0,1,2,3,4,5.
,k=0,1,2,3,4,5.
由此计算ξ的分布列如解法一.
解法三: (Ⅰ)同解法一或解二.
(Ⅱ)由对称性与等可能性,在三层的任一层下电梯的人数同分布,故期望值相等.
即3Eξ=5,从而Eξ=![]() .
.
(19)(本小题13分)
 解法一:
解法一:
(Ⅰ)证:由已知DF∥AB且![]() DAD为直角,故ABFD是矩形,从而CD
DAD为直角,故ABFD是矩形,从而CD![]() BF.
BF.
又PA![]() 底面ABCD,CD
底面ABCD,CD![]() AD,故由三垂线定理知CD
AD,故由三垂线定理知CD![]() PD.在△PDC中,E、F分别
PD.在△PDC中,E、F分别
PC、CD的中点,故EF∥PD,从而CD![]() EF,由此得CD
EF,由此得CD![]() 面BEF. 第(19)图1
面BEF. 第(19)图1
(Ⅱ)连结AC交BF于G.易知G为AC的中点.连接EG,则在△PAC中易知EC∥PA.又因
PA![]() 底面ABCD,故BC
底面ABCD,故BC![]() 底面ABCD.在底面ABCD中,过C作GH
底面ABCD.在底面ABCD中,过C作GH![]() BD,垂足为H,连接EH.由三垂线定理知EH
BD,垂足为H,连接EH.由三垂线定理知EH![]() BD.从而
BD.从而![]() EHG为二面角E-BD-C的平面角.
EHG为二面角E-BD-C的平面角.
 设AB=a,则在△PAC中,有
设AB=a,则在△PAC中,有
BG=![]() PA=
PA=![]() ka.
ka.
以下计算GH,考察底面的平面图(如答(19)图2).连结GD.
因S△CBD=![]() BD·GH=
BD·GH=![]() GB·OF.
GB·OF.
故GH=![]() .
.
在△ABD中,因为AB=a,AD=2A,得BD=![]() a 第(19)图2
a 第(19)图2
而GB=![]() FB=
FB=![]() AD-a.DF-AB,从而得
AD-a.DF-AB,从而得
GH=![]() =
= ![]() =
=![]()
因此tanEHG=![]() =
=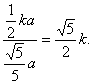
由k>0知![]() 是锐角,故要使
是锐角,故要使![]() >
>![]() ,必须
,必须
![]() >tan
>tan![]() =
=![]()
解之得,k的取值范围为k>![]()
解法二:
(Ⅰ)如图,以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为:轴建立空间直角坐标系,设AB=a,则易知点A,B,C,D,F的坐标分别为
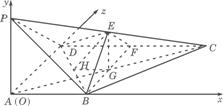 A(0,0,0),B(a,0,0),C(2a,2a,0),D(0,2a,0),
A(0,0,0),B(a,0,0),C(2a,2a,0),D(0,2a,0),
F(a,2a,0).
从而![]() =(2a,0,0),
=(2a,0,0), ![]() =(0,2a,0),
=(0,2a,0),
![]() ·
·![]() =0,故
=0,故![]()
![]()
![]() .
.
设PA=b,则P(0,0,b),而E为PC中点.故 第(19)3
E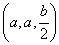 .从而
.从而 =
=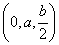 .
.
![]() ·
·![]() =0,故
=0,故![]()
![]()
![]() .
.
由此得CD![]() 面BEF.
面BEF.
(Ⅱ)设E在xOy平面上的投影为G,过G作GH![]() BD垂足为H,由三垂线定理知EH
BD垂足为H,由三垂线定理知EH![]() BD.
BD.
从而![]() EHG为二面角E-BD-C的平面角.
EHG为二面角E-BD-C的平面角.
由PA=k·AB得P(0,0,ka),E![]() ,G(a,a,0).
,G(a,a,0).
设H(x,y,0),则![]() =(x-a,y-a,0),
=(x-a,y-a,0), ![]() =(-a,2a,0),
=(-a,2a,0),
由![]() ·
·![]() =0得=a(x-a)+2a(y-a)=0,即
=0得=a(x-a)+2a(y-a)=0,即
x-2y=-a ①
又因![]() =(x,a,y,0),且
=(x,a,y,0),且![]() 与
与![]() 的方向相同,故
的方向相同,故![]() =
=![]() ,即
,即
2x+y=2a ②
由①②解得x=![]() a,y=
a,y=![]() a,从而
a,从而![]() =
=![]() ,|
,|![]() |=
|=![]() a.
a.
tanEHG=![]() =
=![]() =
=![]() .
.
由k>0知,EHC是锐角,由![]() EHC>
EHC>![]() 得tanEHG>tan
得tanEHG>tan![]() 即
即
![]() >
>![]()
故k的取值范围为k>![]() .
.
(20)(本小题13分)
解:(Ⅰ)求导得f2(x)=[x2+(b+2)x+b+c]ex..
因b2>4(c-1),故方程f2(x)=0即x2+(b+2)x+b+c=0有两根;
x1=-![]() <x2=-
<x2=-![]()
![]()
令f′(x)>0,解得x<x1或x>x1;
又令f′(x)>0,解得x1<x<x2.
故当xε(-, x1)时,f(x)是增函数,当 xε(x2,+)时,f(x)也是增函数,但当xε(x1 , x2)时,f(x)是减函数.
(Ⅱ)易知f(0)=c,f(u)=b+c,因此
![]() .
.
所以,由已知条件得
![]() b+e=4
b+e=4
b2≤4(e-1),
因此b2+4b-12≤0.
解得-6≤b≤2.
(21)(本小题12分)
解:(Ⅰ)因为对任意xεR,有f(f(x)- x2 + x)=f(x)- x2 +x,所以
f(f(2)- 22+2)=f(2)- 22+2.
又由f(2)=3,得f(3-22+2)-3-22+2,即f(1)=1.
若f(0)=a,则f(a-02+0)=a-02+0,即f(a)=a.
(Ⅱ)因为对任意xεR,有f(f(x))- x2 +x)=f(x)- x2 +x.
又因为有且只有一个实数x0,使得f(x0)- x0.
所以对任意xεR,有f(x)- x2 +x= x0.
在上式中令x= x0,有f(x0)-x![]() + x0= x0,
+ x0= x0,
又因为f(x0)- x0,所以x0- x![]() =0,故x0=0或x0=1.
=0,故x0=0或x0=1.
若x0=0,则f(x)- x2 +x=0,即
f(x)= x2 –x.
但方程x2 –x=x有两上不同实根,与题设条件矛质,故x2≠0.
若x2=1,则有f(x)- x2 +x=1,即f(x)= x2 –x+1.易验证该函数满足题设条件.
综上,所求函数为
f(x)= x2 –x+1(x![]() R).
R).
(22)(本小题12分)
证:(1)由题设及椭圆的几何性质有
![]()
设![]()
![]()
因此,由题意![]() 应满足
应满足
![]()
即
即![]() ,
,
从而对任意![]()
(Ⅱ)设点![]()
![]()
![]()
得两极![]() ,从而易知f(c)在(
,从而易知f(c)在(![]() ,
,![]() )内是增函
)内是增函![]() 数,而在(
数,而在(![]() ,1)内是减函数.
,1)内是减函数.
现在由题设取![]() 是增数列.又易知
是增数列.又易知
![]()
![]()
故由前已证,知![]()