高考数学普通高等学校招生全国统一考试
78
本试卷分第I卷（选择题）和第II卷（非选择题）两部分. 共150分. 考试时间120分钟.
第I卷
参考公式：
如果事件A、B互斥，那么
P（A+B）=P(A)+P(B)
如果事件A、B相互独立，那么
P（A·B）=P(A)·P(B)
如果事件A在一次试验中发生的概率是P，那么
n次独立重复试验中恰好发生k次的概率
Pn(k)=C
Pk(1－P)n－k
一、选择题：每小题5分，共60分.
1．已知
为第三象限角，则
所在的象限是 （ ）
A．第一或第二象限 B．第二或第三象限
C．第一或第三象限 D．第二或第四象限
解：α第三象限，即
,
∴
,可知在第二象限或第四象限,选D
2．已知过点A(－2，m)和B(m，4)的直线与直线2x+y-1=0平行，则m的值为 （ ）
A．0 B．－8 C．2 D．10
解：直线2x+y-1=0的一个方向向量为
=(1,-2),
,由
即(m+2)×(-2)-1×(4-m)=0,m=-8,选B
3．在
的展开式中
的系数是 （ ）
A．－14 B．14 C．－28 D．28
解：(x+1)8展开式中x4,x5的系数分别为
,
,∴(x-1)(x+1)8展开式中x5的系数为
,选B
4．设三棱柱ABC-A1B1C1的体积为V，P、Q分别是侧棱AA1、CC1上的点，且PA=QC1，则四棱锥B-APQC的体积为 （ ）
A．
B．
C．
D．
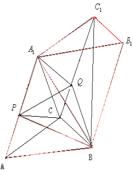解：如图，
,∵AF=QC1,
∴APQC1,APQC都是平行四边形,
∴=
(
)
=
=
,选C
5．设
，则 （ ）
A．－2<x<－1 B．－3<x<－2 C．－1<x<0 D．0<x<1
解：
,
,选A
6．若
，则 （ ）
A．a<b<c B．c<b<a C．c<a<b D．b<a<c
解：由题意得a=
,b=
,c=
,
∵
,∴c<a<b,选C
7．设
,且
,则 （ ）
A．
B．
C．
D．
解：∵由得sinx-cosx=sinx-cosx,又
,
∴,选C
8．
= （ ）
A．
B．
C．1 D．
解：
,选B
9．已知双曲线
的焦点为F1、F2，点M在双曲线上且
则点M到
x轴的距离为 （ ）
A．
B．
C．
D．
解：由
,得MF1⊥MF2,不妨设M(x,y)上在双曲线右支上，且在x轴上方,则有(ex-a)2+(ex+a)2=4c2，即(ex)2+a2=2c2,∵a=1,b=
,c=,e=,得x2=,y2=
,由此可知M点到x轴的距离是
,选C
10．设椭圆的两个焦点分别为F1、、F2，过F2作椭圆长轴的垂线交椭圆于点P，若△F1PF2为
等腰直角三角形，则椭圆的离心率是 （ ）
A．
B．
C．
D．
解：由题意可得
,∵b2=a2-c2e=
,得e2+2e-1=0,∵e>1,解得e=
,选D
11．不共面的四个定点到平面的距离都相等，这样的平面共有 （ ）
A．3个 B．4个 C．6个 D．7
解：共有7个，它们是由四个定点组成的四面体的三对异面直线间的公垂线的三个中垂面；四面体的四条高的四个中垂面，选D
12．计算机中常用十六进制是逢16进1的计数制，采用数字0～9和字母A～F共16个计数
符号，这些符号与十进制的数的对应关系如下表：
| 16进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 10进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
例如，用十六进制表示：E+D=1B，则A×B= （ ）
A．6E B．72 C．5F D．B0
解：∵A=10,B=11,又A×B=10×11=110=16×6+14,∴在16进制中A×B=6E,∴选A
第Ⅱ卷
二．填空题：每小题4分，共（16分）
13．经问卷调查，某班学生对摄影分别执“喜欢”、“不喜欢”和“一般”三种态度，其中执
“一般”态度的比“不喜欢”态度的多12人，按分层抽样方法从全班选出部分学生座
谈摄影，如果选出的5位“喜欢”摄影的同学、1位“不喜欢”摄影的同学和3位执“一
般”态度的同学，那么全班学生中“喜欢”摄影的比全班人数的一半还多 人.
解：设执“不喜欢”的学生为x人，则执“一般”的学生为(x+12)人，由题意得
,x=6,∴执“喜欢”的学生有30人,全班共有人数为12+6+6+30=54(人),∴全班学生中“喜欢”摄影的比全班人数的一半还多3人。
14．已知向量
，且A、B、C三点共线，则k= .
解：
,由题意得(4-k)(-2)-2k×7=0,解得k=
15．曲线
在点（1，1）处的切线方程为
.
解：
,∴曲线在点（1，1）处的切线方程为y-1= -(x-1),即y+x-2=0
16．已知在△ABC中，∠ACB=90°，BC=3，AC=4，P是AB上的点，则点P到AC、BC
的距离乘积的最大值是
解：P到BC的距离为d1,P到AC的距离为d2,则三角形的面积得3d1+4d2=12,∴3d1
4d2≤
,∴d1d2的最大值为3,这时3d1+4d2=12,
3d1=4d2得d1=2,d2=
三.解答题：共74分.
17．(本小题满分12分)
已知函数
求使
为正值的
的集合.
18．(本小题满分12分)
设甲、乙、丙三台机器是否需要照顾相互之间没有影响。已知在某一小时内，甲、
乙都需要照顾的概率为0.05，甲、丙都需要照顾的概率为0.1，乙、丙都需要照顾的概
率为0.125，
（Ⅰ）求甲、乙、丙每台机器在这个小时内需要照顾的概率分别是多少；
（Ⅱ）计算这个小时内至少有一台需要照顾的概率.
19．(本小题满分12分)
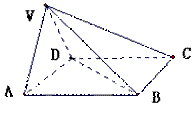
在四棱锥V-ABCD中，底面ABCD是正方形，侧面VAD是正三角形,平面VAD⊥底面ABCD．
（Ⅰ）证明AB⊥平面VAD；
|
20．(本小题满分12分)
在等差数列
中，公差
的等差中项.
已知数列
成等比数列，求数列
的通项
21． (本小题满分12分)
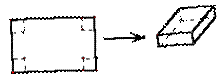
用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小
正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最
大?最大容积是多少?
|
……
22． (本小题满分14分)
设
两点在抛物线
上，
是AB的垂直平分线，
（Ⅰ）当且仅当
取何值时，直线经过抛物线的焦点F？证明你的结论；
（Ⅱ）当
时，求直线的方程.
普通高等学校招生全国统一考试
数学（文）参考答案
一、DBBCA，CCBCD，DA
二、13、3，14、，15、x+y-2=0，16、12
三、解答题：
17．解：∵
……………2分 
………4分
…………………………………………6分
……………………………8分
………………………………………………10分
又
∴
………………………12分
18．解：（Ⅰ）记甲、乙、丙三台机器在一小时需要照顾分别为事件A、B、C，……1分
则A、B、C相互独立，
由题意得： P（AB）=P(A)·P(B)=0.05
P（AC）=P(A)·P(C)=0.1
P（BC）=P(B)·P(C)=0.125…………………………………………………………4分
解得：P(A)=0.2；P(B)=0.25；P(C)=0.5
所以, 甲、乙、丙每台机器在这个小时内需要照顾的概率分别是0.2、0.25、0.5……6分
（Ⅱ）∵A、B、C相互独立，∴
相互独立，……………………………………7分
∴甲、乙、丙每台机器在这个小时内需都不需要照顾的概率为
|
…………………………10分
∴这个小时内至少有一台需要照顾的概率为
……12分
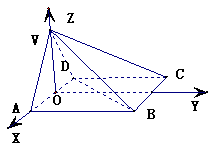
19．证明：（Ⅰ）作AD的中点O，则VO⊥底面
ABCD．…………………………1分
建立如图空间直角坐标系，并设正方形边长为1，…………………………2分
则A（，0，0），B（，1，0），C（-，1，0），D（-，0，0），V（0，0，
），
∴
………………………………3分
由
……………………………………4分
……………………………………5分
又AB∩AV=A ∴AB⊥平面VAD…………………………………………6分
（Ⅱ）由（Ⅰ）得
是面VAD的法向量………………………………7分
设
是面VDB的法向量，则
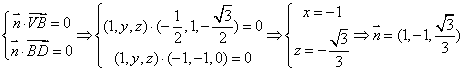……9分
∴
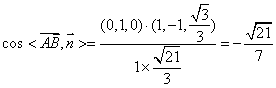，……………………………………11分
又由题意知，面VAD与面VDB所成的二面角，所以其大小为
…………12分
20．解：由题意得：
……………1分 即
…………3分
又
…………4分 又成等比数列,
∴该数列的公比为
，………6分 所以
………8分
又
……………………………………10分
所以数列的通项为
……………………………12分
21．解：设容器的高为x，容器的体积为V，……………………………………………1分
则V=（90－2x）（48－2x）x,(0<V<24)………………………………………………5分
=4x3－276x2+4320x ∵V′=12 x2－552x+4320………………………………7分
由V′=12 x2－552x+4320=0得x1=10，x2=36
∵x<10 时，V′>0, 10<x<36时，V′<0, x>36时，V′>0,
所以,当x=10,V有极大值V(10)=1960………………………………………10分
又V(0)=0,V(24)=0,………………………………………………………………11分
所以当x=10,V有最大值V(10)=1960……………………………………………12分
22．解：（Ⅰ）∵抛物线，即
，
∴焦点为
………………………………………………………1分
（1）直线的斜率不存在时，显然有
………………………………3分
（2）直线的斜率存在时，设为k， 截距为b
即直线：y=kx+b
由已知得：
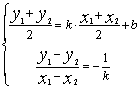……………5分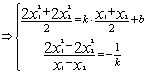 
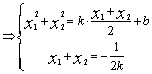……………7分 
即的斜率存在时，不可能经过焦点……………………………………8分
所以当且仅当
=0时，直线经过抛物线的焦点F…………………………9分
（Ⅱ）当
时，
直线的斜率显然存在，设为：y=kx+b………………………………10分
则由（Ⅰ）得：
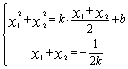
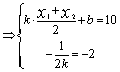………………………11分
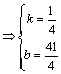…………………………………………13分
所以直线的方程为
，即
………………14分