高考数学普通高等学校招生全国统一考试81
第I卷(选择题 共50分)
一、选择题
1、设集合![]() ,
,![]() ,则
,则![]()
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、若复数![]() (
(![]() 是虚数单位)是纯虚数,则实数
是虚数单位)是纯虚数,则实数![]() 的值为
的值为
A、![]() 2
B、4
C、
2
B、4
C、![]() 6
D、6
6
D、6
3、给出下列三个命题
①
若![]() ,则
,则![]()
② 若正整数![]() 和
和![]() 满足
满足![]() ,则
,则![]()
③ 设![]() 是圆
是圆![]() 上的任意一点,圆
上的任意一点,圆![]() 以
以![]() 为圆心,且半径为1。当
为圆心,且半径为1。当![]() 时,圆
时,圆![]() 与
与![]() 圆相切
圆相切
其中假命题的个数为
A、0 B、1 C、2 D、3
4、设![]() 、
、![]() 、
、![]() 为平面,为
为平面,为![]() 、
、![]() 、
、![]() 直线,则
直线,则![]() 的一个充分条件是
的一个充分条件是
A、![]() B、
B、![]()
C、![]() D、
D、![]()
5、设双曲线以椭圆![]() 长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐进线的斜率为
长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐进线的斜率为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、从集合{1,2,3,…,11}中的任意取两个元素作为椭圆![]() 方程中的
方程中的![]() 和
和![]() ,则能组成落在矩形区域
,则能组成落在矩形区域![]() 内的椭圆的个数是
内的椭圆的个数是
A、43 B、72 C、86 D、90
7、某人射击一次击中的概率是0.6,经过3次射击,此人至少有两次击中目标的概率为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8、要得到![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象上所有的点的
的图象上所有的点的
A、横坐标缩短到原来的![]() 倍(纵坐标不变),再向左平行移动
倍(纵坐标不变),再向左平行移动![]() 个单位长度
个单位长度
B、横坐标缩短到原来的![]() 倍(纵坐标不变),再向右平行移动
倍(纵坐标不变),再向右平行移动![]() 个单位长度
个单位长度
C、横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动![]() 个单位长度
个单位长度
D、横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动![]() 个单位长度
个单位长度
9、设![]() 是函数
是函数![]() 的反函数,则使
的反函数,则使![]() 成立的
成立的![]() 的取值范围为
的取值范围为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、若函数![]() 在区间
在区间![]() 内单调递增,则
内单调递增,则![]() 的取值范围是
的取值范围是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
第Ⅱ卷(非选择题共100分)
二.填空题:本大题共6小题,每小题4分,共24分,把答案填在题中横线上。
11、设![]() ,则
,则![]() __________。
__________。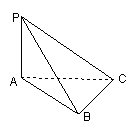
12、若图,![]() 平面
平面![]() ,
,![]() 且
且![]() 则异面直线PB与AC所成角的正切值等于__________。
则异面直线PB与AC所成角的正切值等于__________。
13、在数列![]() 中,
中,![]() ,
,![]() 且
且![]() 则
则![]() __________。
__________。
14、在直角坐标系xOy中,已知点A (0,1)和点B (![]() 3,4),若点C在∠AOB的平分线上且 OC = 2,则OC = __________。
3,4),若点C在∠AOB的平分线上且 OC = 2,则OC = __________。
15、某公司有5万元资金用于投资开发项目,如果成功,一年后可获利12%,一旦失败,一年后将丧失全部资金的50%,下表是过去200例类似项目开发的实施结果:
| 投资成功 | 投资失败 |
| 192次 | 8次 |
则该公司一年后估计可获收益的期望是__________(元)。
16、设![]() 是定义在R上的奇函数,且
是定义在R上的奇函数,且![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() __________。
__________。
三、解答题:本大题共6小题,共76分,解答应写出文字说明,证明过程或演算步骤。
17、(本小题满分12分)
在△ABC中,∠A、∠B、∠C所对的边长分别为a、b、c,设a、b、c满足条件![]() 和
和![]() 。求∠A和
。求∠A和![]() 的值。
的值。
18、(本小题满分12分)
已知:![]() 。
。
(Ⅰ)当a = b时,求数列{![]() }的前n项和
}的前n项和![]() ;
;
(Ⅱ)求![]() 。
。
19、(本小题满分12分)
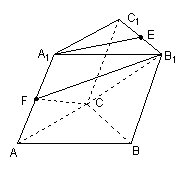
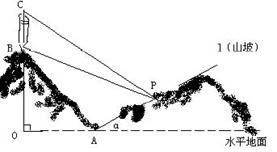
如图,在斜三棱柱![]() 中,
中,![]() ,
,![]() ,侧面
,侧面![]() 与底面ABC所成的二面角为120
与底面ABC所成的二面角为120![]() ,E、F分别是棱
,E、F分别是棱![]() 、
、![]() 的中点。
的中点。
(Ⅰ)求![]() 与底面ABC所成的角;
与底面ABC所成的角;
(Ⅱ)证明EA∥平面![]() ;
;
 (Ⅲ)求经过
(Ⅲ)求经过![]() 、A、B、C四点的球的体积。
、A、B、C四点的球的体积。
20、(本小题满分12)
某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔高BC = 80(米),塔所在的山高OB = 220(米),OA = 200(米),图中所示的山坡可视为直线l且点P在直线l上,l与水平地面的夹角为a,![]() 。试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)。
。试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)。
21、(本题14分)
抛物线C的方程为![]() ,过抛物线C上一点
,过抛物线C上一点 ![]() (
(![]() )作斜率为
)作斜率为![]() 的两条直线分别交抛物线C于
的两条直线分别交抛物线C于![]() ,
,![]() 两点(P、A、B三点互不相同),且满足
两点(P、A、B三点互不相同),且满足![]() (
(![]() ≠0且
≠0且![]() )。
)。
(Ⅰ)求抛物线C的焦点坐标和准线方程
(Ⅱ)设直线AB上一点M,满足![]() ,证明线段PM的中点在y轴上
,证明线段PM的中点在y轴上
(Ⅲ)当![]() 时,若点P的坐标为(1,
时,若点P的坐标为(1,![]() 1),求∠PAB为钝角时点A的纵坐标
1),求∠PAB为钝角时点A的纵坐标![]() 的取值范围。
的取值范围。
22、(本小题满分14分)
设函数![]()
(Ⅰ)证明![]() 其中为k为整数
其中为k为整数
(Ⅱ)设![]() 为
为![]() 的一个极值点,证明
的一个极值点,证明![]()
(Ⅲ)设![]() 在(0,+∞)内的全部极值点按从小到大的顺序排列为
在(0,+∞)内的全部极值点按从小到大的顺序排列为![]() ,证明:
,证明:![]()
2005年普通高等学校招生全国统一考试(天津卷)
数学(理工类)参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | C | B | D | C | B | A | C | A | B |
详细解答过程如下:
1、首先![]() ,否则
,否则![]() 无意义,排除C。取特殊值
无意义,排除C。取特殊值![]() ,排除A、C
,排除A、C
本题答案选D
2、解法一:设![]() ,则
,则![]() ,得:
,得:![]() ,
,![]()
解法二:非零向量![]() ,
,![]() 满足
满足![]() 是纯虚数的意思就是说,这两个非零向量互相垂直。根据题意得:
是纯虚数的意思就是说,这两个非零向量互相垂直。根据题意得:![]() ,从而
,从而![]()
本题答案选C
3、① 用“分部分式”判断,具体:![]() ,又
,又![]() 知本命题为真命题。
知本命题为真命题。
②
用基本不等式:![]() (
(![]() ),取
),取![]() ,
,![]() ,知本命题为真。
,知本命题为真。
③
圆![]() 上存在两个点A、B满足正弦
上存在两个点A、B满足正弦![]() ,所以P、
,所以P、![]() 可能都在圆
可能都在圆![]() 上,当
上,当![]() 在圆
在圆![]() 上时,圆
上时,圆![]() 圆
圆![]() 相交。故本命题假命题。
相交。故本命题假命题。
本题答案选B
4、A选项:缺少条件![]() ;
;
B选项:当![]() 时,
时,![]() ;
;
C选项:当![]() 两两垂直(看着你现在所在房间的天花板上的墙角),
两两垂直(看着你现在所在房间的天花板上的墙角),![]() 时,
时,![]() ;
;
D选项:同时垂直于同一条直线的两个平面平行。本选项为真命题。
本题答案选D
5、双曲线![]() 的两条渐进线是:
的两条渐进线是:![]() 。根据题意:
。根据题意:![]() ,
,![]() ,从而
,从而![]() ,
,![]()
本题答案选C
6、根据题意,![]() 是不大于10的正整数、
是不大于10的正整数、![]() 是不大于8的正整数。但是当
是不大于8的正整数。但是当![]() 时
时![]() 是圆而不是椭圆。先确定
是圆而不是椭圆。先确定![]() ,
,![]() 有8种可能,对每一个确定的
有8种可能,对每一个确定的![]() ,
,![]() 有
有![]() 种可能。故满足条件的椭圆有
种可能。故满足条件的椭圆有![]() 个。
个。
本题答案选B
7、三次射击行为互不影响。击中两次的可能性为![]() ,击中3次的可能性为
,击中3次的可能性为![]() ,经计算
,经计算![]()
本题答案选A
8、![]() 的周期是
的周期是![]() 的周期的2倍,从周期的变化上知道横坐标应该伸长。排除A、B。
的周期的2倍,从周期的变化上知道横坐标应该伸长。排除A、B。
![]() 的横坐标伸长2倍后变成了
的横坐标伸长2倍后变成了![]() ,
,
将![]() 化成正弦形式为
化成正弦形式为![]() ,根据口诀“左加由减”得
,根据口诀“左加由减”得![]() 由
由![]() 向右移动
向右移动![]() 。
。
本题答案选C
9、![]() 时,
时,![]() 单调增函数,所以
单调增函数,所以![]() 。
。
本题答案选A
10、记![]() ,则
,则![]()
当![]() 时,要使得
时,要使得![]() 是增数,则需有
是增数,则需有![]() 恒成立,所以
恒成立,所以![]() 。矛盾。排除C、D
。矛盾。排除C、D
当![]() 时,要使得
时,要使得![]() 是增数,则需有
是增数,则需有![]() 恒成立,所以
恒成立,所以![]() 。
。
排除A
本题答案选B
二、填空题
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 |
|
| 2600 |
| 4760 | 0 |
详细解答过程如下:
11、![]() 所求为:
所求为:![]()
本题答案填写:![]()
12、将此多面体补成正方体![]() ,
,![]() 与
与![]() 所成的角的大小即此正方体主对角线
所成的角的大小即此正方体主对角线![]() 与棱
与棱![]() 所成角的大小。
所成角的大小。![]() 。
。
本题答案填写:![]()
13、当![]() 为奇数时,
为奇数时,![]() ;当
;当![]() 为偶数时,
为偶数时,![]()
因此,数列![]() 的奇数各项都是1,偶数项成公差为2的等差数列
的奇数各项都是1,偶数项成公差为2的等差数列
![]()
本题答案填写:2600
14、设![]() ,则
,则![]() 的终边在第2象限,即
的终边在第2象限,即![]() 且
且![]() ,
,
又![]()
由
![]() ,得
,得![]()
所以:![]() ,
,![]()
![]()
得:![]()
本题答案填写:![]()
15、投资成功的概率是![]() ,失败的概率是
,失败的概率是![]() ,所以所求的数学期望应该是:
,所以所求的数学期望应该是:![]()
本题答案填写:4760
16、![]() 得
得![]()
假设![]()
因为点(![]() ,0)和点(
,0)和点(![]() )关于
)关于![]() 对称,所以
对称,所以![]()
因此,对一切正整数![]() 都有:
都有:![]()
从而:![]()
本题答案填写:0
三、解答题
17、解:![]()
所以:![]()
由:![]()
得:![]()
所以:![]()
18、解:(I)当![]() 时,
时,![]() ,它的前
,它的前![]() 项和
项和
![]() ①
①
①两边同时乘以![]() ,得
,得
![]() ②
②
①
![]() ②,得:
②,得:
![]()
若![]() ,则:
,则:![]()
得: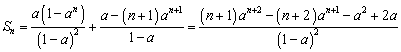
若![]() ,则
,则![]()
(II)当![]() 时,
时,![]()
当![]() 时,设
时,设![]() (
(![]() ),则:
),则:![]()
此时:![]()
当![]() 时,即
时,即![]() 时,
时,![]()
当![]() 时,即
时,即![]() 时,
时,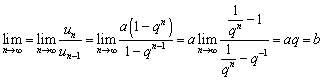
19、(I)解:过![]() 作平面
作平面![]() 平面
平面![]() ,垂足为
,垂足为![]() 。连接
。连接![]() ,并延长
,并延长![]() 交于
交于![]() ,连接
,连接![]() ,于是
,于是![]() 为
为![]() 与底面
与底面![]() 所成的角。
所成的角。
因为![]() ,所以
,所以![]() 为的
为的![]() 平分线
平分线
又因为![]() ,所以
,所以![]() ,
,![]() 且为
且为![]() 的中点
的中点
因此,由三垂线定理![]()
因为![]() ,且
,且![]() ,所以
,所以![]() ,于是为
,于是为![]() 二面角
二面角![]() 的平面角,即
的平面角,即![]()
由于四边形![]() 为平行四边形,得
为平行四边形,得![]()
所以,![]() 与底面
与底面![]() 所成的角度为
所成的角度为![]()
(II) 证明:设![]() 与
与![]() 的交点为
的交点为![]() ,则点P为EG的中点,连结PF。
,则点P为EG的中点,连结PF。
在平行四边形![]() 中,因为F是
中,因为F是![]() 的中点,所以
的中点,所以![]()
而EP![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]()
(III)解:连接![]() 。在△
。在△![]() 和△
和△![]() 中,
中,
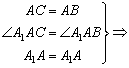 △
△![]() △
△![]()
又因为![]() 平面
平面![]() ,所以
,所以![]() 是△
是△![]() 的外心
的外心
设球心为![]() ,则
,则![]() 必在
必在![]() 上,且
上,且![]()
在Rt△![]() 中,△
中,△
球的体积△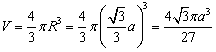
20、解:以O为原点,OA为![]() 轴、OB为
轴、OB为![]() 轴建立直角坐标系,各点坐标为:
轴建立直角坐标系,各点坐标为:![]() (200,0),
(200,0),![]() (0,220),
(0,220),![]() (0,300)
(0,300)
直线![]() 的方程为:
的方程为:![]()
设点P的坐标为(![]() ,
,![]() ) (
) (![]() )
)
直线PC的斜率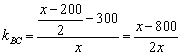
直线PB的斜率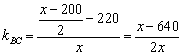
由直线PC到直线PB的角的公式,得
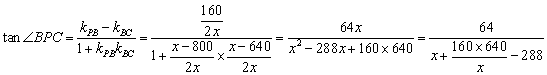
由均值不等式:![]()
当且仅当![]() 时,即
时,即![]() 时上式等号成立,这时,点P的纵坐标为
时上式等号成立,这时,点P的纵坐标为
![]()
当![]() 最大时,
最大时,![]() 最大。
最大。
所以,当此人距地面60米的时,观看铁塔的视角最大。
21、(I)解:由抛物线![]() 的方程
的方程![]() 得,焦点坐标为(
得,焦点坐标为(![]() ),准线方程为
),准线方程为![]()
(II)证明:设直线PA的方程为![]() ,直线PB的方程为
,直线PB的方程为![]()
点![]() 和点
和点![]() 的坐标是方程组
的坐标是方程组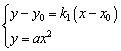 的解
的解
将![]() 代入
代入![]() 得:
得:![]()
由韦达定理:![]() ①
①
同理:![]() ,又因为
,又因为![]() ,所以
,所以![]() ②
②
设点![]() 的坐标为
的坐标为![]() ,由
,由![]() ,得
,得![]() ③
③
将
② 代入 ③ 得:![]()
即:![]() 。所以,线段
。所以,线段![]() 的中点在
的中点在![]() 轴上
轴上
(III)解:因为点P(1,![]() 1)在抛物线
1)在抛物线![]() 上,所以
上,所以![]() ,抛物线的方程为
,抛物线的方程为![]() 。
。
由
① 得:![]() ,代入
,代入![]() 得
得![]()
将![]() 代入 ② ,得
代入 ② ,得![]() ,代入
,代入![]() 得
得![]()
因此,直线PA、PB分别与抛物线C的交点A、B的坐标为
![]()
于是:![]() ,
,![]()
![]()
因为![]() 为钝角且P、A、B三点互不相同,故必有
为钝角且P、A、B三点互不相同,故必有![]() ,即
,即![]()
解得![]() 的范围为:
的范围为:![]() 或
或![]()
又点A的纵坐标![]() 满足
满足![]() ,故
,故
当![]() 时,
时,![]()
当![]() 时,
时,![]()
所以,![]() 为钝角时,点A的纵坐标
为钝角时,点A的纵坐标![]() 的取值范围是
的取值范围是![]()
22、证明:(I)由于函数定义,对任意整数![]() ,有
,有
![]()
(II)函数![]() 在R上可导,
在R上可导,![]() ①
①
令![]() ,得:
,得:![]()
若![]() ,则
,则![]() ,这与
,这与![]() 矛盾,所以
矛盾,所以![]() 。
。
当![]() 时,
时,![]() ②
②
由于函数![]() 的图象和函数
的图象和函数![]() 的图象知,
的图象知,![]() 有解。
有解。
当![]() 时,
时,![]()
(II)证明:由函数![]() 的图象和函数
的图象和函数![]() 的图象知,对于任意整数
的图象知,对于任意整数![]() ,在开区间(
,在开区间(![]() ,
,![]() )内方程
)内方程![]() 只有一个根
只有一个根![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
而![]() 在区间(
在区间(![]() ,
,![]() )内,要么恒正,要么恒负
)内,要么恒正,要么恒负
因此![]() 时
时![]() 的符号与
的符号与![]() 时
时![]() 的符号相反
的符号相反
综合以上,得:![]() 的每一个根都是
的每一个根都是![]() 的极值点 ③
的极值点 ③
由![]() 得,当
得,当![]() 时,
时,![]() ,即对于
,即对于![]() 时,
时,![]() ④
④
综合
③、④ :对于任意![]() ,
,![]()
由:![]() 和
和![]() ,得:
,得:![]() ⑤
⑤
又:![]() ,
,
但![]() 时,
时,![]() ⑥
⑥
综合
⑤、⑥ 得:![]()