高考数学普通高等学校招生全国统一考试82
试题精析详解
一、选择题（5分
10=50分）
（1）
集合
的真子集个数是
（ ）
（A）16 （B）8 （C）7 （D）4
【思路点拨】本题考查集合、真子集的基本概念，可采用直接法求集合A
【正确解答】用列举法，
，A的真子集有：
，共7个，选C
【解后反思】注意不要忘记空集，以及真子集不包含集合本身.
（2）
已知
，则
（ ）
（A）
(B) 
(C) 
(D) 
【思路点拨】本题考查指数函数和对数函数的增减性.
【正确解答】由函数性质可知，函数
在
上是减函数，因此得
，又因为
是增函数，所以，选A
【解后反思】要深刻理解指数函数和对数函数的图象与性质，并从已知条件和结论的特征出发，发现它们各自所具有的模型函数，以便有目的地思考.
（3）某人射击一次击中目标的概率为0.6，经过3次射击，此人至少有两次击中目标的概率为 （ ）
（A）
（B）
（C）
（D）
见理第7题
（4）将直线
沿
轴向左平移1个单位，所得直线与圆
相切，则实数
的值为
（ ）
（A）－3或7 （B）－2或8 （C）0或10 （D）1或11
【思路点拨】本题考查了平移公式、直线与圆的位置关系，只要正确理解平移公式和直线与圆相切的充要条件就可解决.
【正确解答】由题意可知：直线沿轴向左平移1个单位后的直线
为：
.已知圆的圆心为
，半径为
.
解法1：直线与圆相切，则圆心到直线的距离等于圆的半径，因而有
，得
或7.
解法2：设切点为
，则切点满足，即
，代入圆方程整理得：
， （*）
由直线与圆相切可知，（*）方程只有一个解，因而有
，得或7.
解法3：由直线与圆相切，可知
，因而斜率相乘得－1，即
，又因为在圆上，满足方程，解得切点为
或
，又在直线上，解得或7.
选A
【解后反思】直线与圆的位置关系历来是高考的重点.作为圆与圆锥曲线中的特殊图形，具有一般曲线的解决方法外（解法2）还有特别的解法，引起重视理解和掌握.
（5）设
为平面，
为直线，则
的一个充分条件是
（ ）
（A）
（B）
（C）
(D) 
见理第4题
（6）设双曲线以椭圆
长轴的两个端点为焦点，其准线过椭圆的焦点，则双曲线的渐近线的斜率为
（ ）
（A）
2
（B）
（C）
（D）
见理第5题
（7）给出三个命题：
①若
，则
.
②若正整数
和
满足
，则
.
③设
为圆
上任一点，圆
以
为圆心且半径为1．当
时，圆
和相切．
其中假命题的个数为 （ ）
（A）0 （B）1 （C）2 （D）3
见理第3题
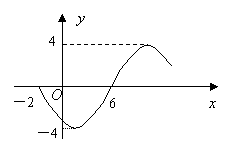
（8）函数
的部分图像如图所示，则函数表达式为
（ ）
（A）
（B）
（C）
（D）
【思路点拨】本题考查正弦曲线的图象变换，考查图与形的等价转换能力. 只要由已知图形依次确定
、
、
，而的确定是解决本题的难点，必须用最高点或最低点进行处理.
【正确解答】解法1：由函数图象可知，函数过点
，振幅
，周期
，频率
，将函数
向右平移6个单位，得到
.选A
解法2：由函数图象可知，函数过点，振幅
，周期，频率，这时
，又因为图象过点
，代入得，
.当
时，
，而
,
当
时，
，而
,无解.
.选A.
解法3：可将点的坐标分别代入进行筛选得到.选A.
【解后反思】一般地，如果由图象来求正弦曲线的解析式时，其参数、、的确定：由图象的最高点或最低点求振幅，由周期或半个周期（相邻最值点的横坐标间的距离）确定，考虑到的唯一性，在确定、的基础上将最值点的坐标代入正弦函数的解析式，在给定的区间内求出的值.
（9）若函数
在区间
，内恒有
，则
的单调递增区间为
（ ）
（A）
（B）
（C）
（D）
【思路点拨】本题考查二次函数对数函数的性质，区间的题意就是要研究出
的值域来判定a的取值范围.
【正确解答】函数的定义域为
，在区间上，
，又，则
，因此
是减函数，函数的单调递增区间为函数的递减区间，考虑对数函数的定义域，得所求的单调递增区间为
选D
【解后反思】对复合函数的性质，一方面要考虑定义域，另一方面要有借助函数图象，用数形结合的思想来解决问题.
（10）设式定义在
上以6为周期的函数，在
内单调递减，且
的图像关于直线
对称，则下面正确的结论是
（ ）
（A）
（B）
（C）
（A）
【思路点拨】本题考查函数的周期性，单调性和对称性等性质，对相关概念有深刻的理解，将自变量的值转化到同一个单调区间，借助图象进行处理.
【正确解答】函数图象关于直线对称，则有
，因此有
，又因为函数周期为6，因此
，
在内单调递减，所以，选B
【解后反思】直观的几何图形是解决问题的有效的重要方法之一，必须引起重视.
二、填空题（4分6=24分）
（11）二项式
的展开式中常数项为
．
【思路点拨】本题考查二项式定理的通项公式，只要概念清楚和运算无误即可.
【正确解答】展开式的一般项为
，令
，
，因此常数项为
.
【解后反思】要注意符号因子不能丢.
（12）已知
，
和
的夹角为
，以，为邻边作平行四边形，则此平行四边形的两条对角线中较短的一条的长度为
．
【思路点拨】本题以向量为背景，考查余弦定理，要判断较短的一条应是所对的对角线.
【正确解答】
【解后反思】要正确向量的加减法则的几何意义，对向量=（x,y）的模有几种方法.①
②
.
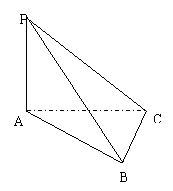（１３）如图，
，
，
则异面直线
与
所成的角的正切值等于
．
见理第12题
（1４）在数列
中，
，且
，则
．
见理第13题
（15）设函数
，则函数
的定义域为
．
【思路点拨】本题考查复合函数定义域的求法，必须使常见各类函数都有意义，构成不等式组来解.
【正确解答】由题意得
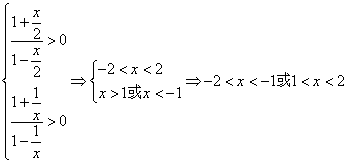则所求定义域为
.
【解后反思】正确地解不等式组，将繁分式化简是一关键.
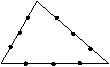
（16）在三角形的每条边上各取三个分点（如图）．以
这9个分点为顶点可画出若干个三角形，若从中
任意抽取一个三角形，则其三个顶点分别落在原
三角形的三个不同边上的概率为 .
【思路点拨】本题考查等可能事件的概率，关键是要确定基本事件.
【正确解答】可画出的三角形个数为
，三个顶点分别落在不同边上的个数为
，所求概率为
.
【解后反思】理解和掌握等可能事件的概率的计算公式P（A）＝
，本题中构成三角形的个数是一难点.
三、解答题（共6小题，共76分）
（17）（本小题满分12分）
已知
，求
及
．
【思路点拨】本题以三角函数的求值问题考查三角变换能力和运算能力，可从已知角和所求角的内在联系（均含
）进行转换得到.
【正确解答】解法一：由题设条件，应用两角差的正弦公式得
，即
①
由题设条件，应用二倍角余弦公式得
故
②
由①和②式得
，
因此，
，由两角和的正切公式
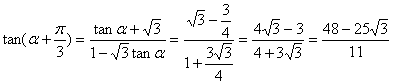
解法二：由题设条件，应用二倍角余弦公式得
，
解得 
，即
由
可得
由于
，且
，故a在第二象限于是，
从而
以下同解法一
【解后反思】在求三角函数值时，必须对各个公式间的变换应公式的条件要理解和掌握，注意隐含条件的使用，以防出现多解或漏解的情形.
（18）（本小题满分12分）
若公比为
的等比数列的首项
且满足
．
（I）求的值；
（II）求数列
的前项和
．
【思路点拨】本题考查等比数列的通项公式及前n项和的求法.可根据其定义进行求解，要注意①等比数列的公比C是不为零的常数②前n项和的公式是关于n的分段函数，对公比C是否为1加以讨论.
【正确解答】(Ⅰ)解：由题设，当
时，
，
，
由题设条件可得
，因此
，即
解得c＝1或
(Ⅱ)解：由(Ⅰ)，需要分两种情况讨论，
当c＝1时，数列是一个常数列，即
(nÎN*)
这时，数列的前n项和
当时，数列是一个公比为
的等比数列，即
(nÎN*)
这时，数列的前n项和
①
① 式两边同乘，得
②
①式减去②式，得
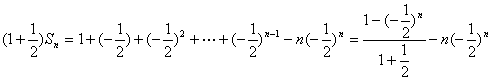
所以
(nÎN*)
【解后反思】本题是数列求和及极限的综合题.
（1）完整理解等比数列
的前n项和公式：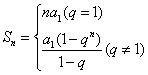
（2）要掌握以下几种情形的极限的求法.①利用
②利用
（
）③要掌握分类讨论的背景转化方法.如
时转化为
.
（19）（本小题满分12分）
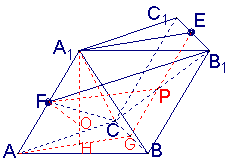如图，在斜三棱柱
中，
，
侧面
与底面
所成的二面角为
，
分别是棱
的中点
（I）求
与底面所成的角；
（II）证明
；
（III）求经过
四点的球的体积．
见理第19题
（20）（本小题满分12分）
某人在山坡
点处观看对面山顶上的一座铁塔，如图所示，塔高
米，塔所在的山高
米，
米，图中所示的山坡可视为直线且点在直线上，与水平面的夹角为
．试问，此人距水平地面多高时，观看塔的视角
最大（不计此人身高）？
见理第20题
（21）（本小题满分14分）
已知
，设
：
和
是方程
的两个实根，不等式
对任意实数
恒成立；
：函数
在
上有极值．
求使正确且正确的的取值范围．
【思路点拨】本题是组合题，考查一元二次方程的根的概念和导数的应用.
【正确解答】 (Ⅰ)由题设和是方程的两个实根，得
+＝
且＝－2，
所以，
当Î[-1,1]时，
的最大值为9，即
£3
由题意，不等式
对任意实数Î[1,1]恒成立的m的解集等于不等式
的解集由此不等式得
①
或 
②
不等式①的解为
不等式②的解为
或
因为，对或或时，P是正确的
(Ⅱ)对函数
求导
令
，即
此一元二次不等式的判别式
若D＝0，则有两个相等的实根
，且
的符号如下：
|
| (－¥, |
| ( |
| + | 0 | + |
因为，
不是函数的极值
若D>0，则有两个不相等的实根和 (<)，且的符号如下：
| x | (－¥, |
| ( |
| ( |
|
| + | 0 | － | 0 | + |
因此，函数f()在＝处取得极大值，在＝处取得极小值
综上所述，当且仅当D>0时，函数f()在(－¥,+¥)上有极值
由
得
或
，
因为，当或时，Q是正确得
综上，使P正确且Q正确时，实数m的取值范围为(-¥,1)È
【解后反思】对恒成立问题的等价转换，相应知识的完整理解是关键.对P来说，转化为求使
的最大值时的范围，而要注意一次二次方程根存在的充要条件.对Q来说，
的导函数存在的充要条件的理解是一难点，也是易错点.
（22）（本小题满分14分）
抛物线
的方程为
，过抛物线上的一点
作斜率为
的两条直线分别交抛物线于
两点（
三点互不相同），且满足
．
（I）求抛物线的焦点坐标和准线方程；
（II）设直线
上一点
，满足
，证明线段
的中点在
轴上；
（III）当
时，若点的坐标为（1，－1），求
为钝角时点的纵坐标
的取值范围．
见理第22题.